Cara menghitung z score pada kalkulator ti-84

Skor-z memberi tahu kita berapa banyak deviasi standar suatu nilai tertentu dari mean. Skor-z dari nilai tertentu dihitung sebagai berikut:

skor-z = (x – μ) / σ

Emas:

• x: nilai individu
• μ: rata-rata populasi
• σ: deviasi standar populasi

Tutorial ini menjelaskan cara menghitung skor-z pada kalkulator TI-84.

Cara menghitung skor Z dari satu nilai

Misalkan suatu distribusi berdistribusi normal dengan rata-rata 12 dan simpangan baku 1,4 dan kita ingin menghitung skor-z dari nilai individual x = 14. Untuk menghitung skor-z dalam kalkulator TI-84, kita cukup ketik rumus berikut:

Ini memberitahu kita bahwa nilai individu 14 memiliki skor-z 1,4286 . Dengan kata lain, nilai 14 berada pada standar deviasi 1,4286 di atas mean.

Cara menghitung skor Z dari beberapa nilai

Sebagai gantinya, misalkan kita memiliki daftar nilai data dan kita ingin menghitung skor-z untuk setiap nilai dalam daftar tersebut. Dalam hal ini kita dapat melakukan langkah-langkah berikut:

Langkah 1: Masukkan datanya.

Pertama, kita akan memasukkan nilai data. Tekan Stat lalu tekan EDIT . Masukkan nilai berikut pada kolom L1:

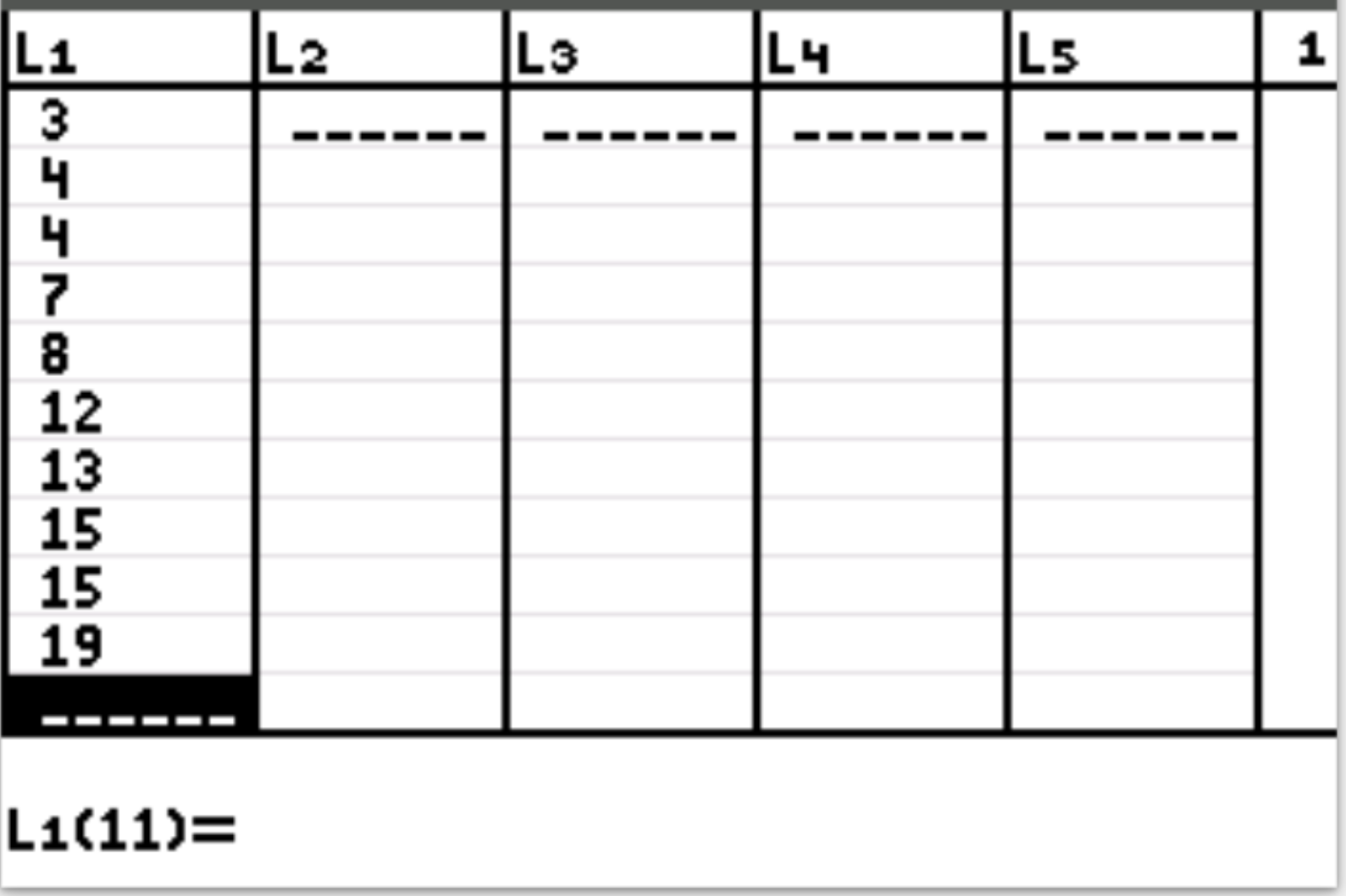
Langkah 2: Temukan mean dan deviasi standar dari nilai data.

Selanjutnya kita akan mencari mean dan deviasi standar dari dataset tersebut. Tekan Stat lalu gulir ke CALC . Sorot Statistik 1-Var dan tekan Enter .

Untuk List , pastikan L1 dipilih karena ini adalah kolom tempat kita memasukkan data. Biarkan FreqList kosong. Sorot Hitung dan tekan Enter .

Output berikut akan muncul:

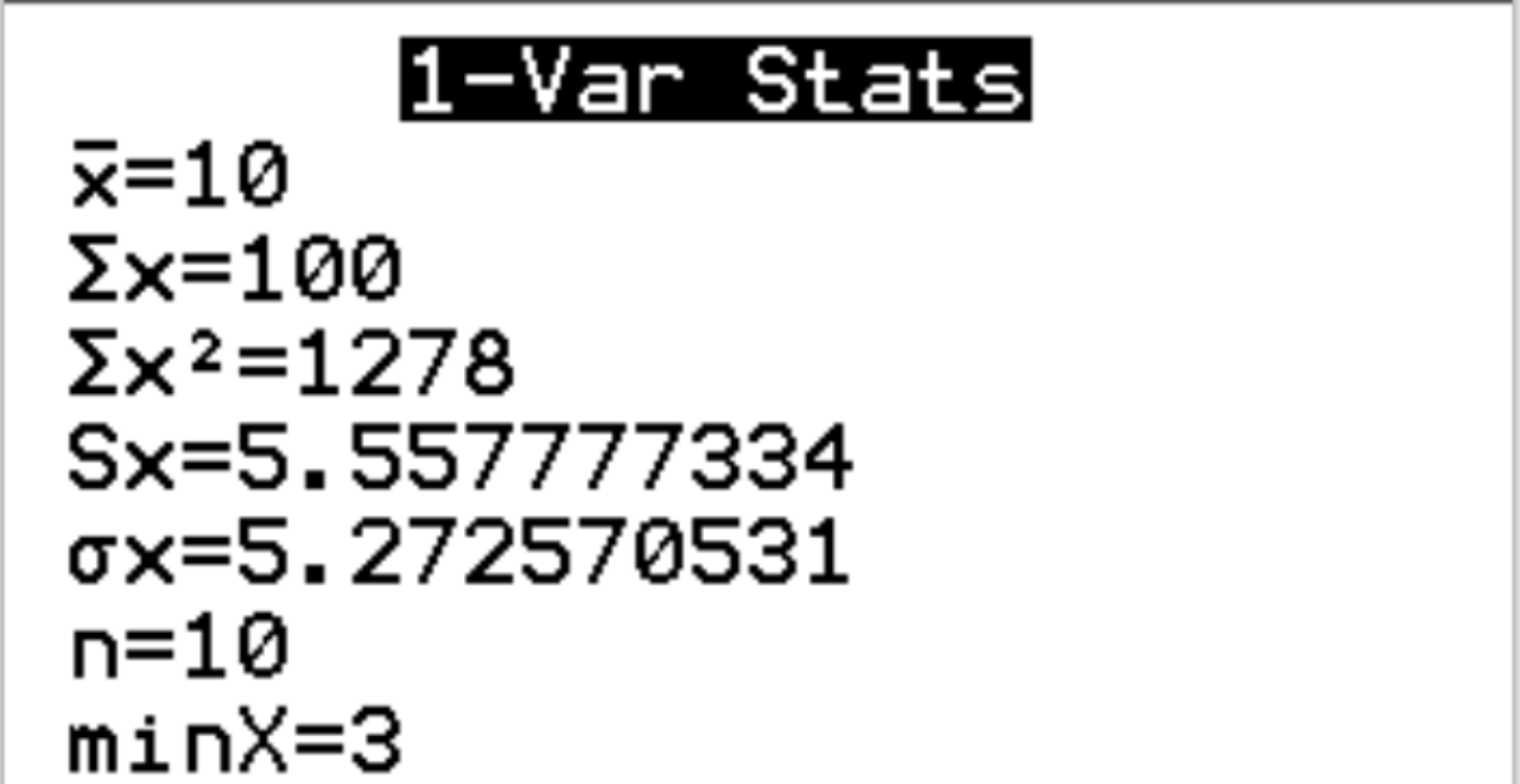
Kita dapat melihat bahwa mean dari dataset tersebut adalah x = 10 dan standar deviasinya adalah s _x = 5.558 . Kami akan menggunakan kedua nilai ini pada langkah berikutnya untuk menghitung skor-z.

Langkah 3: Gunakan rumus untuk menghitung setiap skor-z.

Selanjutnya, kita akan menghitung skor-z untuk setiap nilai individual dalam kumpulan data. Tekan Stat lalu tekan EDIT . Sorot L2 dan ketikkan rumusnya ( L1-10)/5.558 , lalu tekan Enter . Skor-z dari setiap nilai individu akan otomatis muncul di kolom L2:

Catatan: Untuk memasukkan “L1” ke dalam rumus, tekan 2 , lalu tekan 1 .

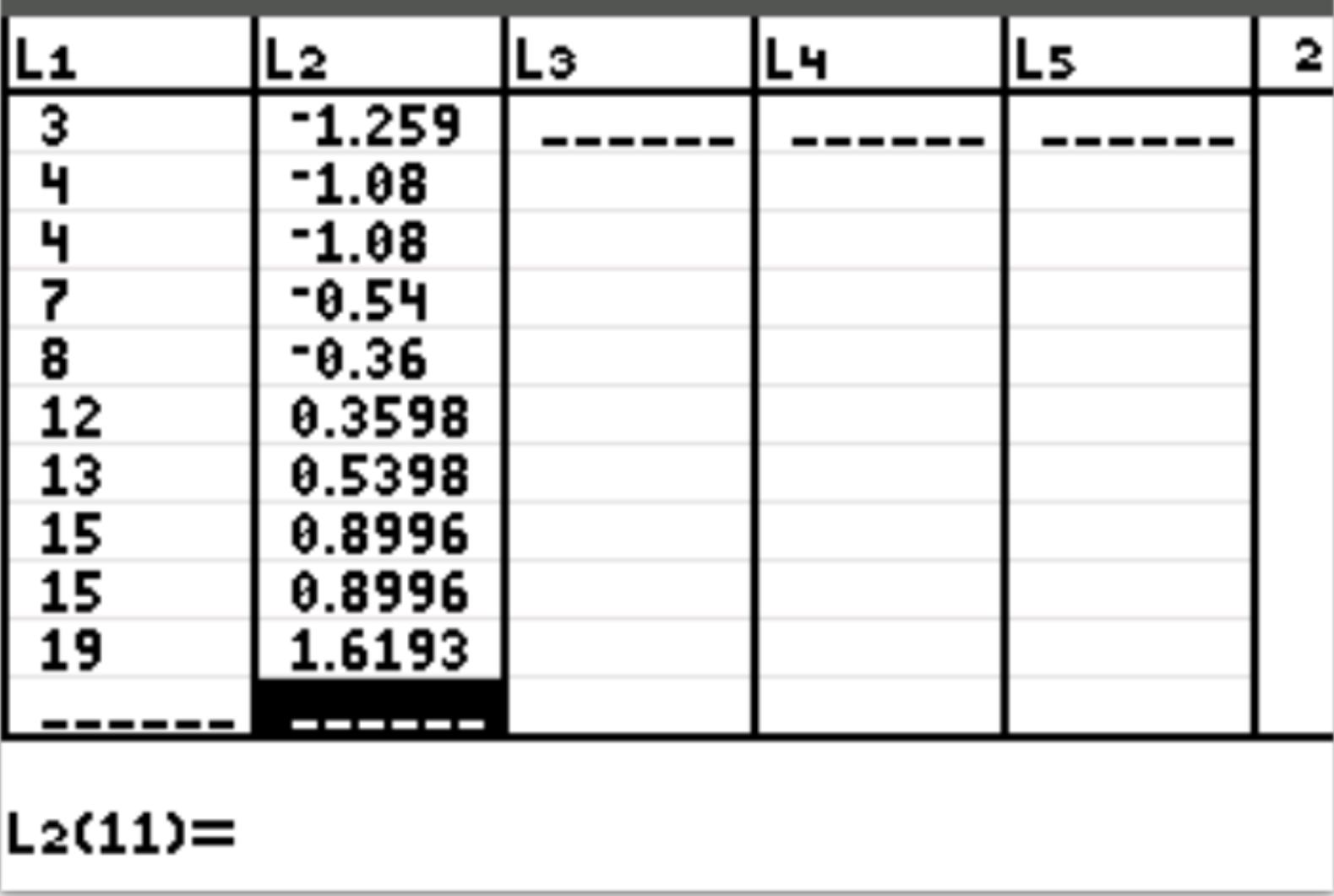
Bagaimana menafsirkan skor Z

Ingatlah bahwa skor-z hanya memberi tahu kita berapa banyak deviasi standar suatu nilai dari mean. Skor z bisa positif, negatif, atau sama dengan nol:

• Skor z yang positif menunjukkan bahwa suatu nilai tertentu berada di atas rata-rata.
• Skor z negatif menunjukkan bahwa nilai tertentu berada di bawah rata-rata.
• Skor z nol menunjukkan bahwa nilai tertentu sama dengan mean.

Dalam contoh kita, kita menemukan bahwa rata-ratanya adalah 10 dan deviasi standarnya adalah 5,558 .

Jadi nilai pertama dalam dataset kita adalah 3, yang memiliki skor z (3-10)/5.558 = -1.259 . Artinya nilai “3” lebih rendah standar deviasinya sebesar 1,259 dari mean.

Nilai berikutnya dalam kumpulan data kami, 4, memiliki skor-z (4-10) / 5.558 = -1.08 . Artinya nilai “4” lebih rendah standar deviasinya sebesar 1,08 dari mean.

Semakin jauh suatu nilai dari mean, semakin tinggi nilai absolut skor-z untuk nilai tersebut.

Misalnya, nilai 3 lebih jauh dari mean dibandingkan nilai 4, yang menjelaskan mengapa 3 memiliki skor-z dengan nilai absolut lebih besar.