Uji z dua proporsi: definisi, rumus dan contoh
Uji z dua proporsi digunakan untuk menguji perbedaan antara dua proporsi populasi.
Tutorial ini menjelaskan hal berikut:
- Motivasi untuk melakukan uji z dua proporsi.
- Rumus untuk melakukan uji z dua proporsi.
- Contoh cara melakukan uji z dua proporsi.
Tes Z dua proporsi: motivasi
Misalkan kita ingin mengetahui apakah ada perbedaan antara proporsi penduduk yang mendukung undang-undang tertentu di Kabupaten A dan proporsi yang mendukung undang-undang di Kabupaten B.
Karena terdapat ribuan penduduk di setiap daerah, maka akan memakan waktu dan biaya yang terlalu besar untuk berkeliling dan mensurvei setiap penduduk di setiap daerah.
Sebagai gantinya, kita dapat mengambil sampel acak sederhana dari penduduk dari setiap daerah dan menggunakan proporsi yang mendukung hukum di setiap sampel untuk memperkirakan perbedaan proporsi yang sebenarnya antara kedua daerah tersebut:
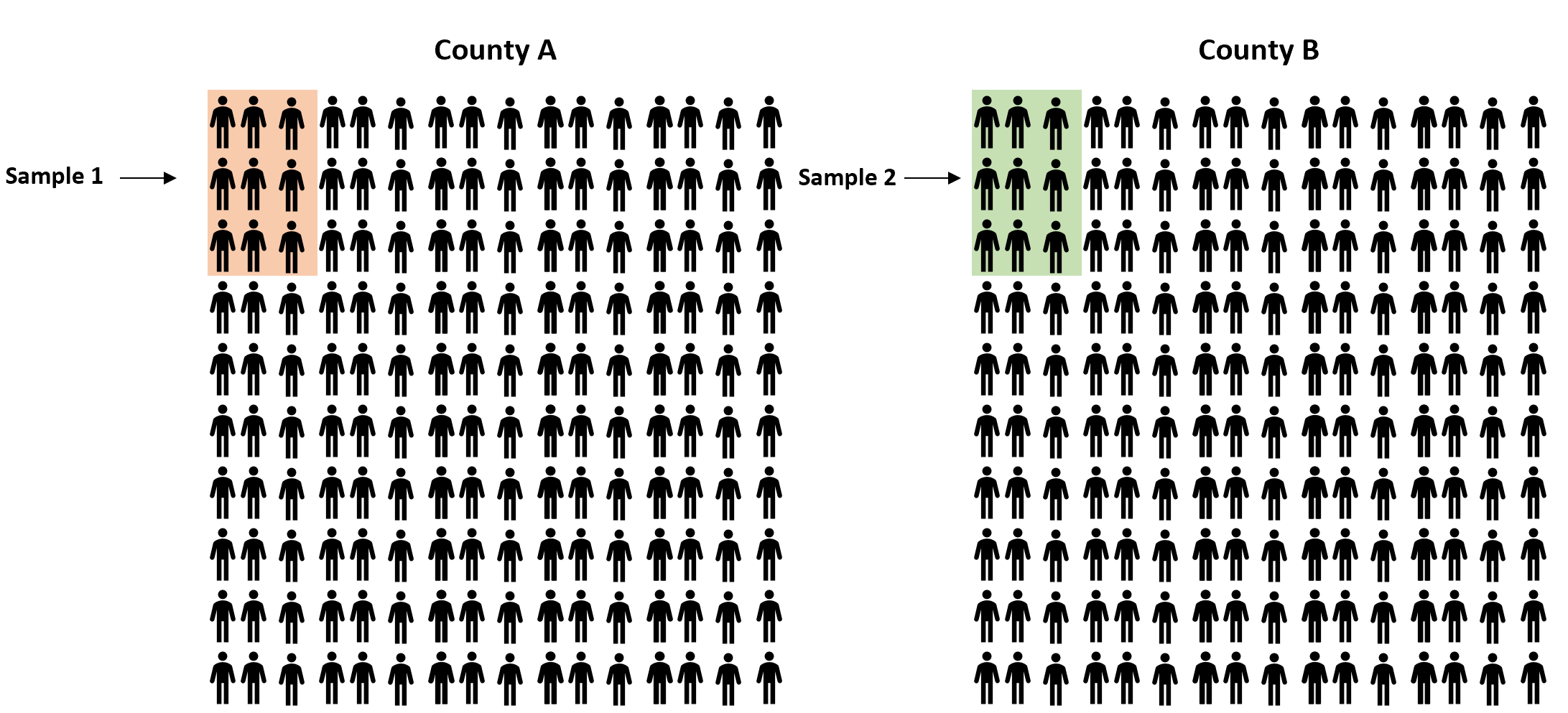
Namun, dapat dipastikan bahwa proporsi penduduk yang mendukung undang-undang tersebut setidaknya akan sedikit berbeda di antara kedua sampel tersebut. Pertanyaannya adalah apakah perbedaan ini signifikan secara statistik . Untungnya, uji z dua proporsi memungkinkan kita menjawab pertanyaan ini.
Uji Z dua proporsi: rumus
Uji-z dua proporsi selalu menggunakan hipotesis nol berikut:
- H 0 : μ 1 = μ 2 (proporsi kedua populasi sama)
Hipotesis alternatif dapat bersifat bilateral, kiri atau kanan:
- H 1 (dua sisi): π 1 ≠ π 2 (proporsi kedua populasi tidak sama)
- H 1 (kiri): π 1 < π 2 (proporsi penduduk 1 lebih kecil dibandingkan proporsi penduduk 2)
- H 1 (kanan): π 1 > π 2 (proporsi penduduk 1 lebih besar dibandingkan proporsi penduduk 2)
Kami menggunakan rumus berikut untuk menghitung statistik uji z:
z = (p 1 -p 2 ) / √ p(1-p)(1/n 1 +1/n 2 )
dimana p 1 dan p 2 adalah proporsi sampel, n 1 dan n 2 adalah ukuran sampel, dan dimana p adalah total proporsi gabungan yang dihitung sebagai berikut:
p = (p 1 n 1 + p 2 n 2 )/(n 1 + n 2 )
Jika nilai p yang sesuai dengan statistik uji z lebih kecil dari tingkat signifikansi yang dipilih (pilihan umum adalah 0,10, 0,05, dan 0,01), maka Anda dapat menolak hipotesis nol.
Uji Z dengan dua proporsi : contoh
Misalkan kita ingin mengetahui apakah ada perbedaan antara proporsi penduduk yang mendukung undang-undang tertentu di Kabupaten A dan proporsi yang mendukung undang-undang di Kabupaten B.
Untuk mengujinya, kita akan melakukan uji z dua proporsi pada tingkat signifikansi α = 0,05 dengan menggunakan langkah-langkah berikut:
Langkah 1: Kumpulkan data sampel.
Misalkan kita mengumpulkan sampel acak penduduk dari setiap daerah dan memperoleh informasi berikut:
Contoh 1:
- Ukuran sampel n 1 = 50
- Proporsi yang mendukung hukum p 1 = 0,67
Contoh 2:
- Ukuran sampel n 2 = 50
- Proporsi yang mendukung hukum p 2 = 0,57
Langkah 2: Tentukan asumsi.
Kami akan melakukan uji z dua proporsi dengan hipotesis berikut:
- H 0 : π 1 = π 2 (proporsi kedua populasi sama)
- H 1 : π 1 ≠ π 2 (proporsi kedua populasi tidak sama)
Langkah 3: Hitung statistik uji z .
Pertama, kita akan menghitung total proporsi gabungan:
p = (p 1 n 1 + p 2 n 2 )/(n 1 +n 2 ) = (0,67(50) + 0,57(50))/(50+50) = 0,62
Selanjutnya kita akan menghitung statistik uji z :
z = (p 1 -p 2 ) / √ p(1-p)(1/n 1 +1/n 2 ) = (.67-.57) / √ .62(1-.62)(1/50 + 1/50 ) = 1,03
Langkah 4: Hitung nilai p dari statistik uji z .
Menurut kalkulator skor-Z nilai-P, nilai-p dua sisi yang terkait dengan z = 1,03 adalah 0,30301 .
Langkah 5: Buatlah kesimpulan.
Karena nilai p ini tidak lebih rendah dari tingkat signifikansi α = 0,05, kami gagal menolak hipotesis nol. Kami tidak memiliki cukup bukti untuk mengatakan bahwa proporsi penduduk yang mendukung undang-undang ini berbeda di kedua wilayah tersebut.
Catatan: Anda juga dapat melakukan seluruh uji Z dua proporsi ini hanya dengan menggunakan kalkulator uji Z dua proporsi .
Sumber daya tambahan
Tutorial berikut menjelaskan cara melakukan uji z dua proporsi menggunakan berbagai perangkat lunak statistik:
Cara melakukan tes Z dua proporsi di Excel
Cara melakukan tes Z dua proporsi di SAS
Kalkulator Uji Z Dua Proporsi