Come eseguire il test di dunnett in r

Un test post hoc è un tipo di test eseguito a seguito di un’ANOVA per determinare quali medie di gruppo differiscono l’una dall’altra in modo statisticamente significativo.

Se uno dei gruppi di studio è considerato il gruppo di controllo , allora dovremmo utilizzare il test di Dunnett come test post-hoc.

Questo tutorial spiega come eseguire il test Dunnett in R.

Esempio: test di Dunnett in R

Supponiamo che un insegnante voglia sapere se due nuove tecniche di studio hanno il potenziale per migliorare i punteggi dei test dei suoi studenti. Per verificarlo, divide casualmente la sua classe di 30 studenti nei seguenti tre gruppi:

• Gruppo di controllo: 10 studenti
• Nuovo studio tecnico 1: 10 studenti
• Nuovo studio tecnico 2: 10 studenti

Dopo una settimana di utilizzo della tecnica di studio assegnata, ogni studente sostiene lo stesso esame.

Possiamo utilizzare i seguenti passaggi in R per creare un set di dati, visualizzare le medie del gruppo, eseguire un’ANOVA unidirezionale e infine eseguire il test di Dunnett per determinare quale nuova tecnica di studio (se presente) produce risultati diversi rispetto al gruppo di controllo .

Passaggio 1: crea il set di dati.

Il codice seguente mostra come creare un set di dati contenente i risultati degli esami di tutti i 30 studenti:

 #create data frame
data <- data.frame(technique = rep (c("control", "new1", "new2"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 control 76
2 controls 77
3 controls 77
4 controls 81
5 controls 82
6 controls 82

Passaggio 2: visualizza i risultati dell’esame per ciascun gruppo.

Il codice seguente mostra come produrre boxplot per visualizzare la distribuzione dei risultati degli esami per ciascun gruppo:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

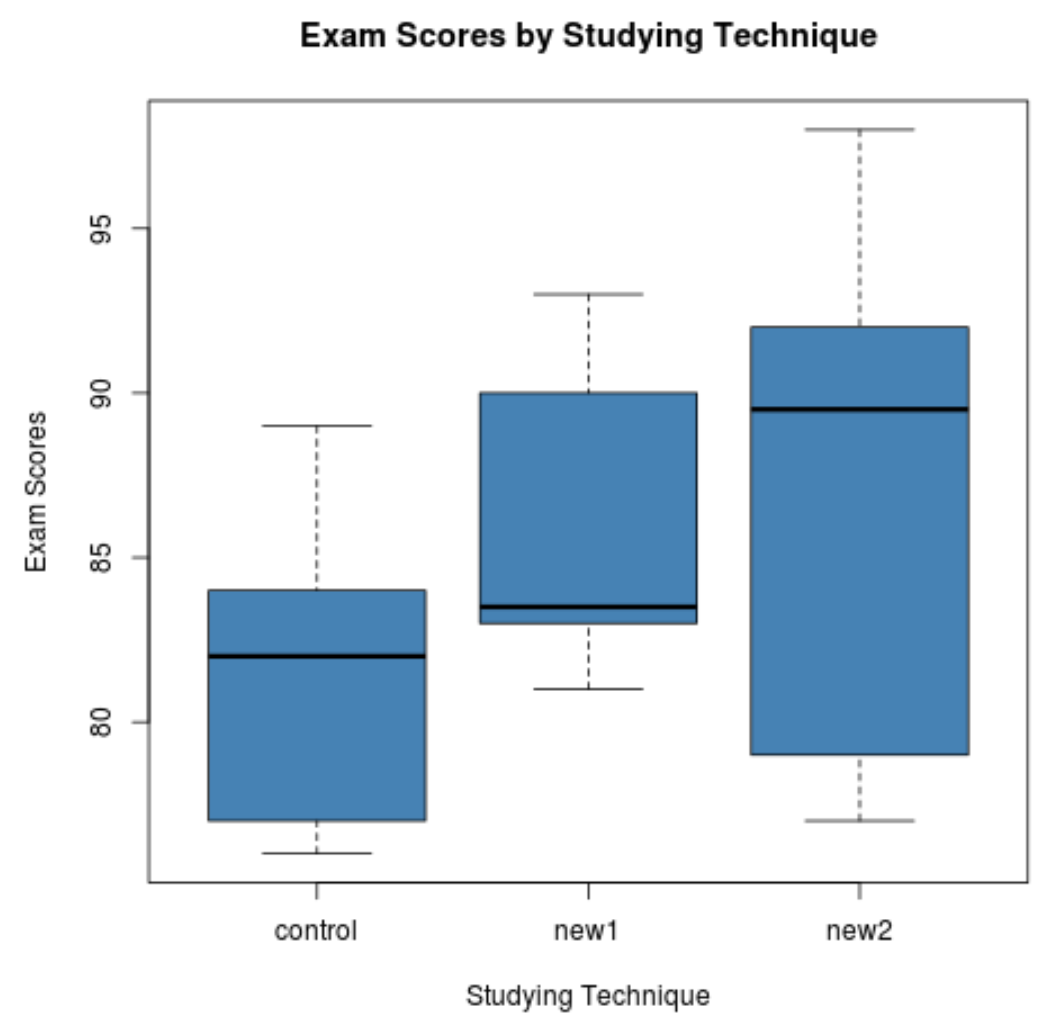
Proprio dai box plot possiamo vedere che la distribuzione dei punteggi degli esami è molto diversa per ciascuna tecnica di studio. Eseguiremo quindi un’ANOVA unidirezionale per determinare se queste differenze sono statisticamente significative.

Correlati: Come tracciare più box plot in un singolo grafico in R

Passaggio 3: eseguire un’ANOVA unidirezionale.

Il codice seguente mostra come eseguire un’ANOVA unidirezionale per verificare le differenze tra i punteggi medi degli esami in ciascun gruppo:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Poiché il valore p complessivo ( 0,0476 ) è inferiore a 0,05, ciò indica che ciascun gruppo non ha lo stesso punteggio medio dell’esame. Successivamente, eseguiremo il test Dunnett per determinare quale tecnica di studio produce punteggi medi degli esami che differiscono da quelli del gruppo di controllo.

Passaggio 4: eseguire il test di Dunnett.

Per eseguire il test Dunnett in R possiamo utilizzare la funzione DunnettTest() della libreria DescTools che utilizza la seguente sintassi:

Test di Dunnett(x, g)

Oro:

• x: un vettore numerico di valori di dati (es. risultati degli esami)
• g: Un vettore che specifica i nomi dei gruppi (es. tecnica di studio)

Il codice seguente mostra come utilizzare questa funzione per il nostro esempio:

 #load DescTools library
library(DescTools)

#perform Dunnett's Test
DunnettTest(x=data$score, g=data$technique)

  Dunnett's test for comparing several treatments with a control:  
    95% family-wise confidence level

$control
             diff lwr.ci upr.ci pval    
new1-control 4.2 -1.6071876 10.00719 0.1787    
new2-control 6.4 0.5928124 12.20719 0.0296 *  

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1' '1.' 0.1 ' ' 1

Il modo di interpretare il risultato è il seguente:

• La differenza media nei punteggi degli esami tra la nuova tecnica di studio 1 e il gruppo di controllo è 4,2. Il valore p corrispondente è 0,1787 .
• La differenza media nei punteggi degli esami tra la nuova tecnica di studio 2 e il gruppo di controllo è 6,4. Il valore p corrispondente è 0,0296 .

Sulla base dei risultati, possiamo vedere che lo studio della Tecnica 2 è l’unica tecnica che produce punteggi medi degli esami significativamente (p = 0,0296) diversi da quelli del gruppo di controllo.

Risorse addizionali

Un’introduzione all’ANOVA unidirezionale
Come eseguire l’ANOVA unidirezionale in R
Come eseguire il test di Tukey in R