Funzione di distribuzione

Di Benjamin anderson Agosto 5, 2023 Probabilità 0 commenti

In questo articolo troverai la spiegazione della funzione di distribuzione, come vengono calcolati i suoi valori e un esempio reale della funzione di distribuzione. Inoltre, sarai in grado di vedere le differenze tra una funzione di distribuzione e una funzione di densità.

Qual è la funzione di distribuzione?

La funzione di distribuzione , chiamata anche funzione di distribuzione cumulativa , è una funzione matematica che indica la probabilità cumulativa di una distribuzione. Cioè, l’immagine della funzione di distribuzione per qualsiasi valore è uguale alla probabilità che la variabile assuma quel valore o un valore inferiore.

La funzione di distribuzione cumulativa può essere indicata anche con l’acronimo FDA, sebbene il suo simbolo abituale sia la F maiuscola.

La funzione di distribuzione è quindi definita dalla seguente formula:

$F(x)=P[X\leq x]$

Come calcolare la funzione di distribuzione

Spiegheremo poi come calcolare il valore della funzione di distribuzione a seconda che la distribuzione di probabilità sia discreta o continua.

Scatola discreta

Se la variabile casuale è discreta, la funzione di distribuzione cumulativa è uguale alla somma delle probabilità di tutti i valori uguali o inferiori a x .

$\displaystyle F(x)=P[X\leq x]=\sum_{u\leq x}f(u)$

Oro

$f(u)$

è la funzione di probabilità associata alla variabile discreta.

Caso continuo

Se la variabile casuale è continua, la funzione di distribuzione cumulativa è equivalente all’integrale della funzione di densità da meno infinito al valore in questione.

$\displaystyle F(x)=P[X\leq x]=\int_{-\infty}^{x}f(u)du$

Oro

$f(u)$

è la funzione di densità associata alla variabile continua.

Esempio di funzione di distribuzione

Ora che conosciamo la definizione di funzione di distribuzione, diamo un’occhiata a un esempio pratico passo passo per imparare a calcolare il valore di una funzione di distribuzione.

Calcola la funzione di distribuzione per l’esperimento casuale di lanciare una moneta quattro volte.

Per risolvere l’esercizio, devi prima calcolare tutte le probabilità legate al numero di teste ottenute durante i quattro lanci della moneta:

Quindi, trattandosi di una variabile discreta, per determinare le immagini della funzione di distribuzione è sufficiente sommare le probabilità fino al valore della variabile in questione:

$\begin{array}{l}F(X\leq 0)=f(0)=0,0625\\[4ex]\begin{aligned}F(X\leq 1)& =f(0)+f(1)\\[1.1ex] & =0,0625+0,25=0,3125\end{aligned}\\[6ex]\begin{aligned}F(X\leq 2)& =f(0)+f(1)+f(2)\\[1.1ex] & =0,0625+0,25+0,375=0,6875\end{aligned}\\[6ex]\begin{aligned}F(X\leq 3)& =f(0)+f(1)+f(2)+f(3)\\[1.1ex] & =0,0625+0,25+0,375+0,25=0,9375\end{aligned}\\[6ex]\begin{aligned}F(X\leq 4)& =f(0)+f(1)+f(2)+f(3)+f(4)\\[1.1ex] & =0,0625+0,25+0,375+0,25+0,0625=1\end{aligned}\end{array}$

Pertanto, i valori della funzione di distribuzione del lancio della testa lanciando quattro monete indipendenti sono i seguenti:

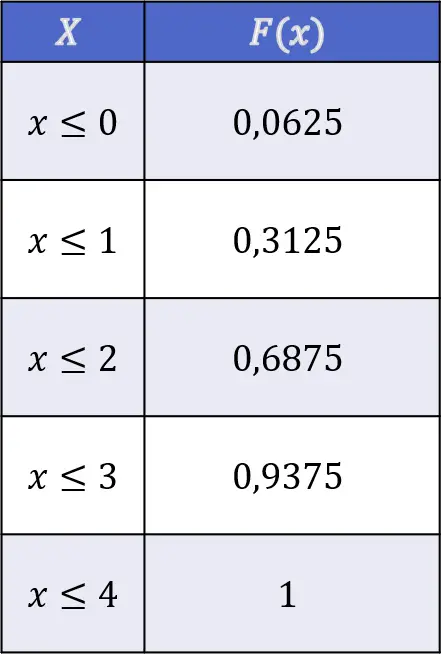
Proprietà della funzione di distribuzione

Indipendentemente dal tipo di variabile, la funzione di distribuzione ha sempre le seguenti proprietà:

Il valore della funzione di distribuzione cumulativa è compreso tra 0 e 1 inclusi.

$0\leq F(x) \leq 1$

Il limite di una funzione di distribuzione quando x tende all’infinito è uguale a 1.

$\displaystyle\lim_{x\to +\infty} F(x)=1$

D’altra parte, il limite di una funzione di distribuzione quando x si avvicina a meno infinito è zero.

$\displaystyle\lim_{x\to -\infty} F(x)=0$

Per le sue caratteristiche, la funzione di distribuzione è monotona e non decrescente.

$x_1 \leq x_2 \implies F(x_1)\leq F(x_2)$

Inoltre, se
$a\leq b$

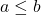
sono soddisfatte le seguenti equazioni.

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}P(X < a) = F(a^-)\\[2ex] P(X>a)=1-F(a)\\[2ex]P(X \ge a )=1-F(a^-)\\[2ex]P(a<ul><li> Finally, if the statistical variable is continuous, the following equality is satisfied: </li></ul>[latex ]\begin{array}{l}P(a \le X < b) = \displaystyle\int_{a}^{b}f(x)\,dx = F(b)- F(a)\end{array}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ... the statistical variable is continuous, the
Please use \mathaccent for accents in math mode.
leading text: ...iable statistic is continuous, equality
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}

Funzione di distribuzione e funzione di densità

Infine, vedremo qual è la differenza tra la funzione di distribuzione e la funzione di densità, poiché queste due nozioni statistiche vengono spesso confuse.

La differenza tra la funzione di distribuzione e la funzione di densità è il tipo di probabilità che definiscono. La funzione di densità descrive la probabilità che la variabile assuma un certo valore, mentre la funzione di distribuzione descrive la probabilità cumulativa della variabile.

Cioè, la funzione di distribuzione viene utilizzata per calcolare la probabilità che la variabile sia uguale o inferiore a un determinato valore.

Si noti che la funzione di densità si riferisce solo a variabili continue, quindi questa distinzione ha senso solo se la variabile studiata è continua.

Notate come cambia la rappresentazione grafica della funzione di distribuzione rispetto alla funzione di densità di una variabile che segue una distribuzione normale con media pari a 1 e deviazione standard pari a 0,5:

differenza tra funzione di distribuzione e funzione di densità

Per ulteriori informazioni sulla funzione di densità, vedere il seguente articolo:

➤ Vedi: funzione di densità

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più