Cos'è la restrizione dell'ambito?

Spesso nelle statistiche si cerca di misurare la correlazione tra due variabili. Questo ci aiuta a comprendere quanto segue:

• La direzione della relazione tra due variabili. All’aumentare di una variabile, l’altra variabile tende ad aumentare o a diminuire?
• La forza della relazione tra due variabili. Di quanto cambia il valore delle due variabili?

Sfortunatamente, un problema che può sorgere quando si misura la correlazione tra due variabili è chiamato restrizione dell’intervallo . Ciò si verifica quando l’ intervallo dei valori misurati per una delle variabili è limitato per qualche motivo.

Ad esempio, supponiamo di voler misurare la correlazione tra le ore di studio e i punteggi degli esami degli studenti di una particolare scuola.

Se raccogliamo dati su queste due variabili per tutti i 1.000 studenti della scuola, potremmo scoprire che la correlazione tra le ore studiate e i punteggi degli esami è 0,73 .

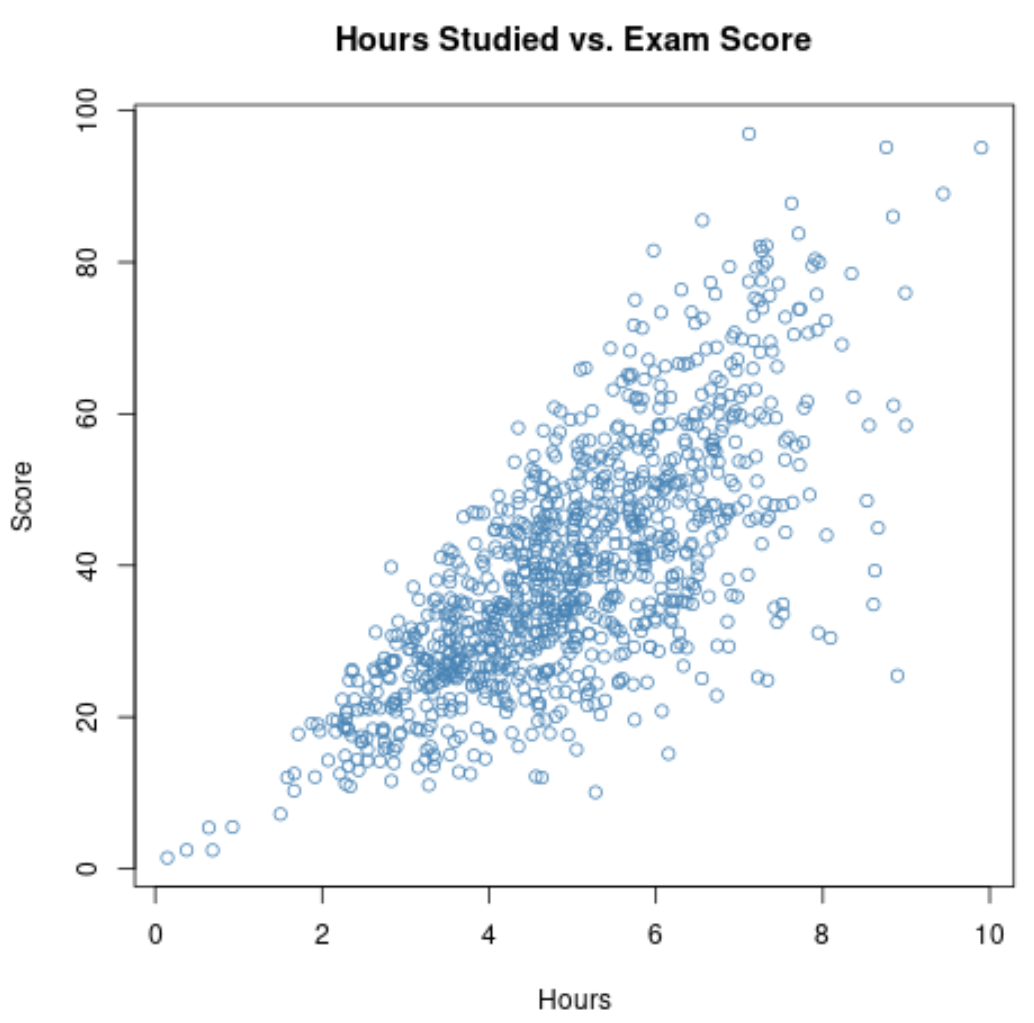
Questa correlazione è piuttosto elevata, indicando una forte relazione positiva tra le due variabili. Man mano che gli studenti studiano di più, tendono ad ottenere risultati migliori negli esami.

Tuttavia, supponiamo di raccogliere dati solo sugli studenti dei corsi con lode. Potrebbe darsi che tutti questi studenti abbiano studiato per almeno 6 ore.

Pertanto, se calcolassimo la correlazione tra le ore studiate e i punteggi degli esami per questi studenti, utilizzeremmo un intervallo ristretto per le ore studiate variabili .

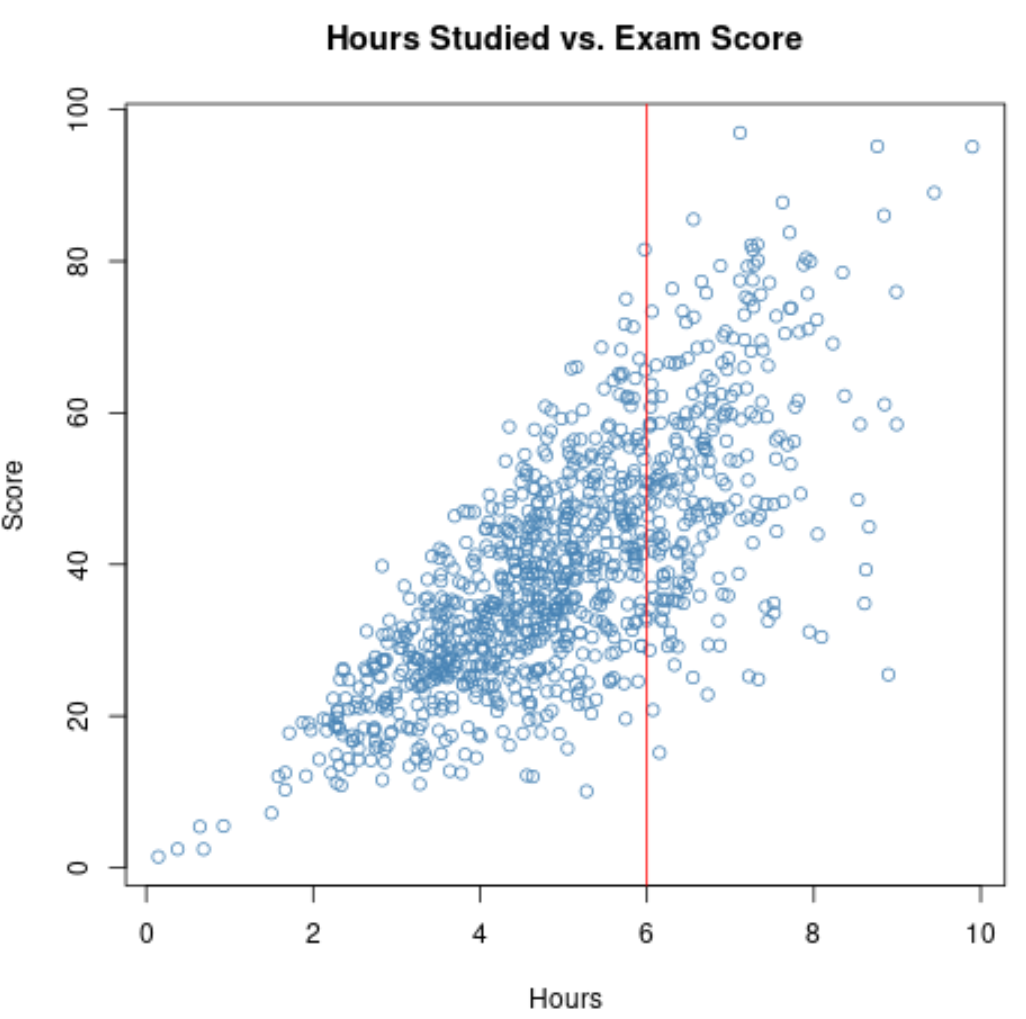
Se ingrandiamo il grafico a dispersione per l’intervallo in cui le ore sono maggiori di 6, ecco come appare il grafico:

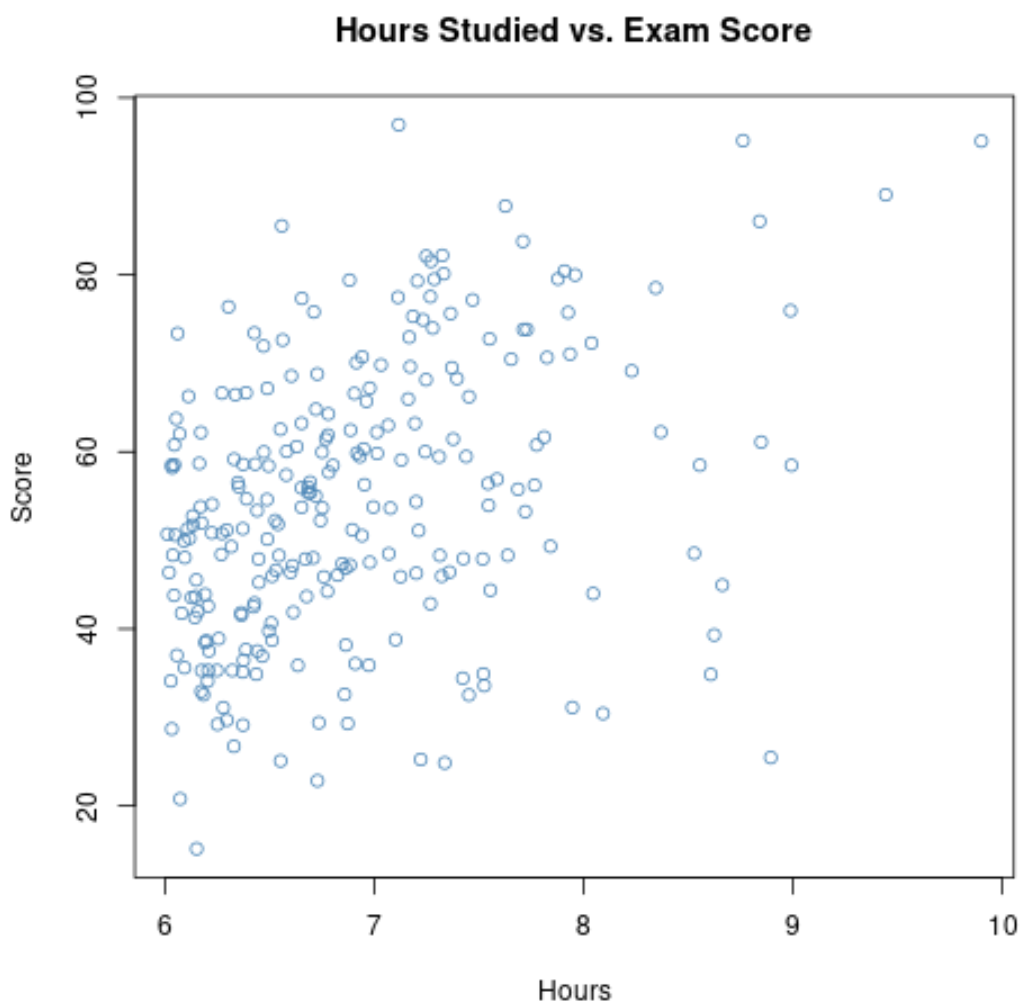
La correlazione tra le due variabili su questo grafico risulta essere 0,37 , che è significativamente inferiore a 0,73 .

Pertanto, se raccogliessimo dati solo sulle ore studiate e sui punteggi degli esami per gli studenti dei corsi con lode, potremmo supporre che esista una relazione debole tra le ore studiate e i punteggi degli esami.

Tuttavia, questo risultato sarebbe fuorviante poiché abbiamo utilizzato un intervallo ristretto per una delle variabili.

Esempi reali di portata limitata

Il problema di un intervallo ristretto può sorgere nella pratica in molti studi di ricerca diversi. Ecco alcuni esempi:

1. Studi su atleti ad alte prestazioni . I ricercatori potrebbero essere interessati a studiare se un determinato programma di allenamento produce più massa muscolare rispetto a un determinato programma standard.

Se i ricercatori raccogliessero dati solo sugli atleti d’élite, è probabile che questi atleti abbiano già un’elevata massa muscolare. Ci sarà quindi un ristretto range di valori a disposizione per calcolare la correlazione tra programma di allenamento e massa muscolare prodotta.

2. Studi su studenti con risultati elevati. I ricercatori potrebbero voler studiare se un determinato programma di tutoraggio ha o meno un effetto positivo sui voti. Per natura, gli studenti desiderosi di migliorare i propri voti e partecipare al programma di tutoraggio potrebbero già essere studenti con ottimi risultati.

Quindi potrebbe non esserci molto margine di miglioramento nei voti di questi studenti. Quando i ricercatori calcolano la correlazione tra le ore trascorse nel programma di tutoraggio e il conseguente aumento di voto, la vera correlazione potrebbe essere sottostimata perché lo spazio per il miglioramento del voto è stato limitato.

Come tenere conto degli intervalli limitati

Un modo popolare per tenere conto degli intervalli ristretti è noto come Thorndike Case 2 , una formula sviluppata dallo psicometrico Robert L. Thorndike.

Questa formula fornisce una stima della vera correlazione tra due variabili e utilizza il seguente calcolo:

Correlazione vera = √(1-(SD ² _{y ristretto} -SD ² _{y non limitato} )) * (1-r ² _ristretto )

Oro:

• SD ² _{limitato y} : la deviazione standard quadrata dei dati disponibili sulla variabile di risposta y.
• SD ² anni _{senza restrizioni} : la deviazione standard quadrata nota della variabile di risposta per la popolazione.
• r ² _ristretto : la correlazione quadratica sui dati ristretti disponibili.

Questa formula ha dimostrato di essere efficace nel produrre stime imparziali della vera correlazione tra due variabili quando una delle variabili soffre di un intervallo ristretto.

Tieni presente che per utilizzare questa formula, devi disporre di una stima della deviazione standard effettiva della popolazione per la variabile di risposta.