Un'introduzione alla distribuzione triangolare

La distribuzione triangolare è una distribuzione di probabilità continua con una funzione di densità di probabilità a forma di triangolo.

È definito da tre valori:

• Il valore minimo ha
• Il valore massimo b
• Il valore massimo c

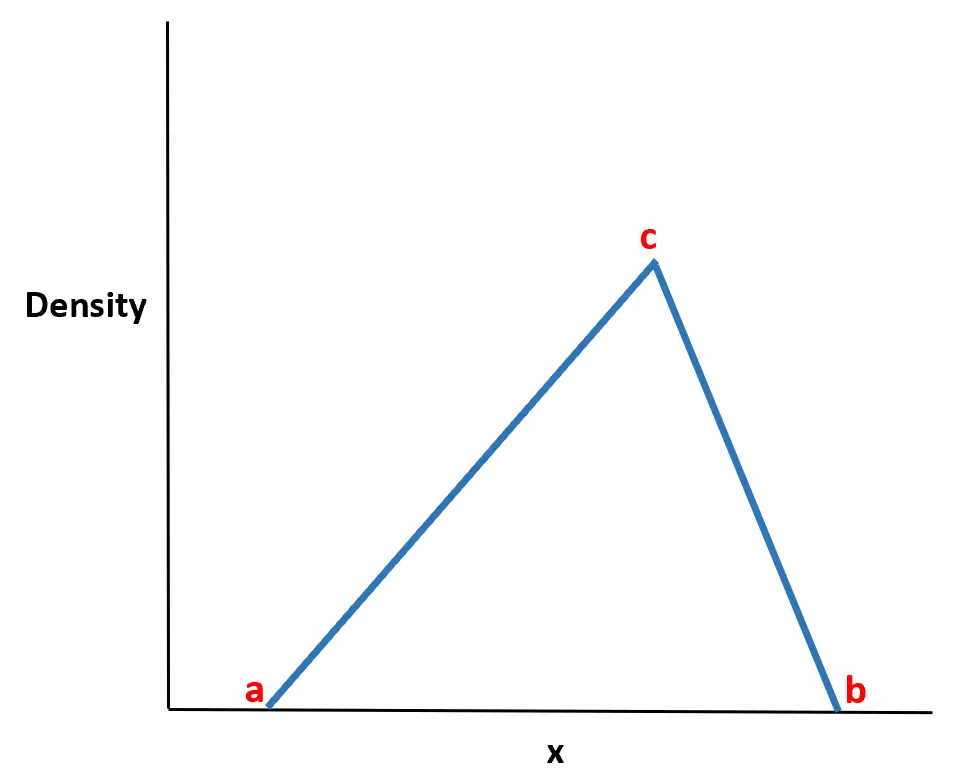
Il nome della distribuzione deriva dal fatto che la funzione di densità di probabilità ha la forma di un triangolo.

Si scopre che questa distribuzione è estremamente utile nel mondo reale perché spesso possiamo stimare il valore minimo (a), il valore massimo (b) e il valore più probabile (c) che assumerà una variabile casuale . può spesso modellare il comportamento delle variabili casuali utilizzando una distribuzione triangolare conoscendo solo questi tre valori.

Ad esempio, un ristorante potrebbe stimare che le sue vendite totali per la prossima settimana saranno pari ad un minimo di $ 10.000, un massimo di $ 30.000 e molto probabilmente $ 25.000.

Utilizzando solo questi tre numeri, potrebbero utilizzare una distribuzione triangolare per determinare la probabilità di realizzare un certo numero di vendite.

Proprietà della distribuzione triangolare

La distribuzione triangolare ha le seguenti proprietà:

PDF:

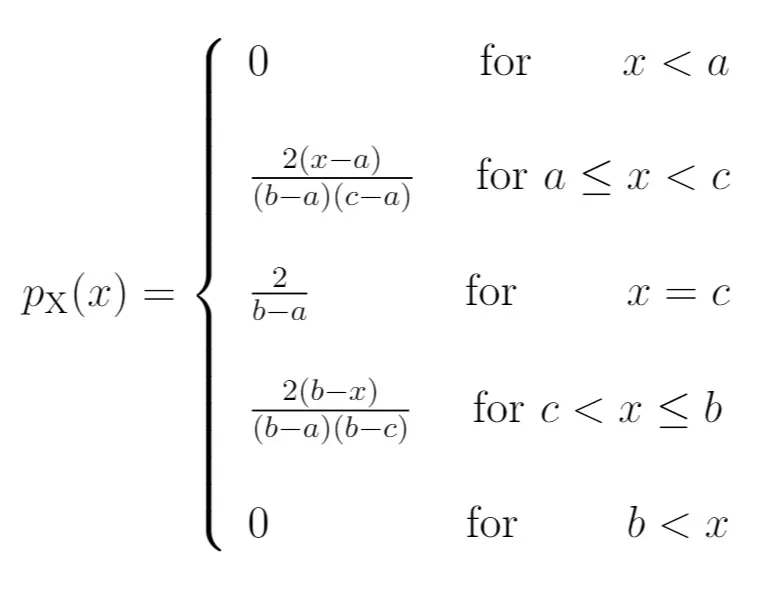
CDF:

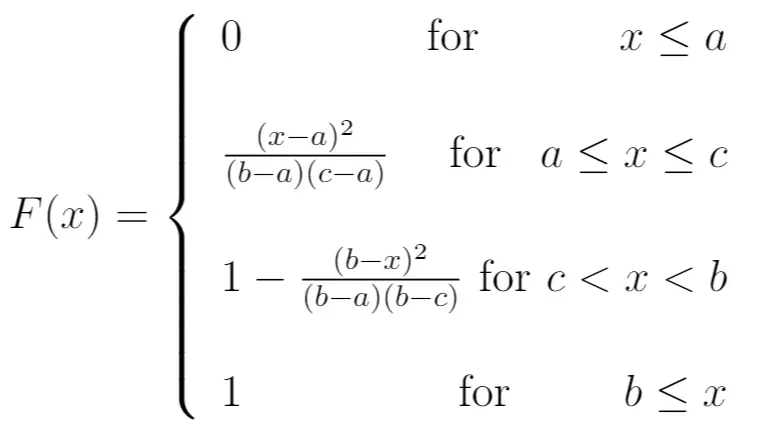
Media: (a + b + c) / 3

Modalità: c

Varianza: (a ² + b ² + c ² – ab – ac – bc) / 18

Esempio di utilizzo della distribuzione triangolare

Torniamo all’esempio precedente. Supponiamo che un ristorante stimi che le sue vendite totali per la prossima settimana saranno un minimo di $ 10.000, un massimo di $ 30.000 e molto probabilmente $ 25.000.

Qual è la probabilità che il ristorante abbia un fatturato totale inferiore a $ 20.000?

Per rispondere a questa domanda, possiamo chiedere x = vendite totali. Sappiamo che x è compreso tra il valore minimo a di $ 10.000 e il valore massimo c di $ 25.000.

Quindi, secondo il PDF, possiamo utilizzare la seguente equazione per trovare la probabilità che il ristorante abbia meno di $ 20.000 di vendite totali:

• P(X < $ 20.000) = (xa) ² / ((ba)(ca))
• P(X < $ 20.000) = (20.000-10.000) ² / ((30.000-10.000)(25.000-10.000))
• P(X < $ 20.000) = 0,333

La probabilità che il ristorante abbia un fatturato totale inferiore a $ 20.000 è 0,333 .

Qual è la vendita media prevista per il ristorante?

Possiamo calcolare le vendite medie previste utilizzando la formula per la media fornita in precedenza:

• Media = (a + b + c) / 3
• Media = ($ 10.000 + $ 30.000 + $ 25.000) / 3
• Media = $ 21.667

Le vendite medie previste sono 21.667 .

Risorse addizionali

I seguenti tutorial forniscono introduzioni ad altre distribuzioni comunemente utilizzate:

La distribuzione normale
La distribuzione binomiale
La distribuzione dei pesci
La distribuzione geometrica