Diagramma ad albero

Questo articolo spiega cos’è un diagramma ad albero e come è realizzato. Troverai quindi esempi di strutture ad albero, i vantaggi di questo tipo di diagramma e, inoltre, un esercizio risolto passo dopo passo.

Cos’è un albero?

Un diagramma ad albero , chiamato anche albero delle probabilità , è una rappresentazione grafica di tutti i possibili risultati di un esperimento insieme alle loro probabilità.

Pertanto, viene utilizzato un diagramma ad albero per rappresentare graficamente tutti i possibili risultati in uno spazio campionario e calcolarne le probabilità.

Un diagramma ad albero è realizzato in modo tale che ogni risultato ( nodo ) si dirama in nuovi possibili risultati ( rami ) fino al raggiungimento dei risultati finali.

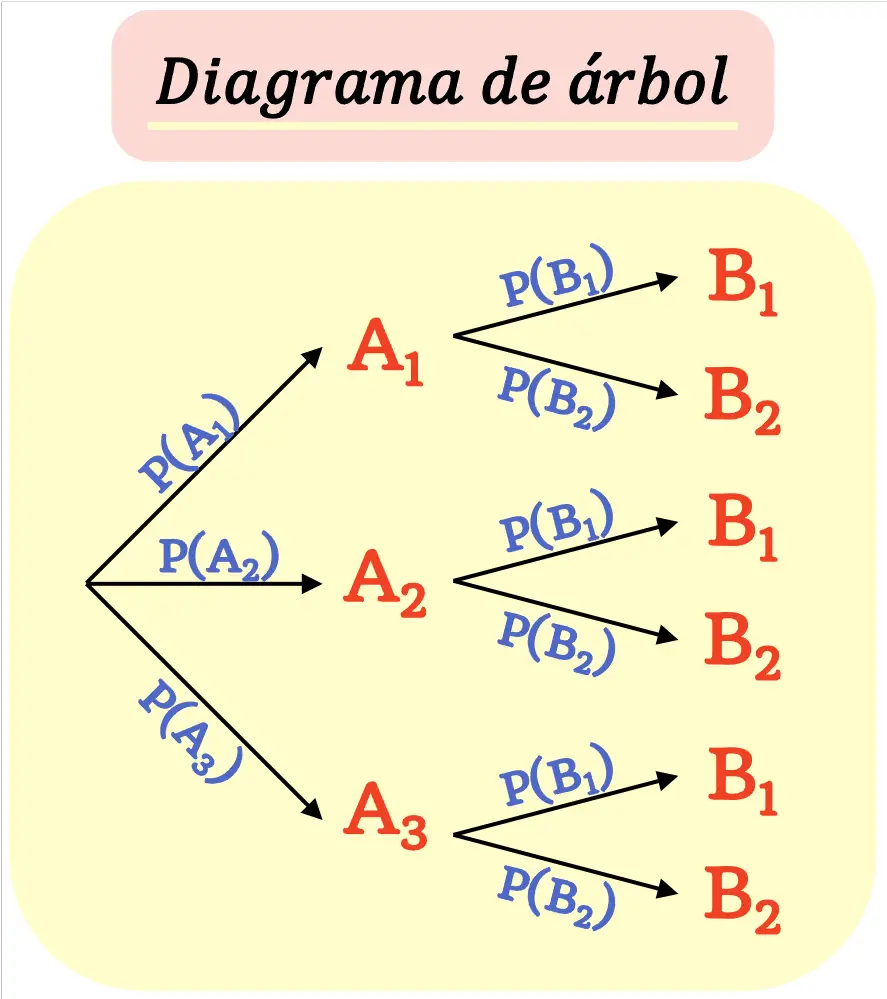
Va tenuto presente che la somma delle probabilità di tutti i rami che escono da un nodo deve essere uguale a 1.

Come realizzare un diagramma ad albero

Per creare un albero è necessario seguire i seguenti passaggi:

1. Il primo passo nella creazione di un diagramma ad albero è disegnare un ramo per ogni possibile risultato. Questi saranno i rami di prima generazione.
2. Quindi, la probabilità associata a ciascun evento viene aggiunta al ramo corrispondente.
3. La fine di ogni ramo di prima generazione è un nodo da cui devono essere rappresentati i rami dei successivi possibili eventi.
4. Come nei primi rami bisogna sommare le probabilità degli eventi rappresentati.
5. Ripeti i passaggi 3 e 4 fino a raggiungere i nodi finali, ovvero le possibili conclusioni dell’esperimento.

Si noti che il numero di filiali in un livello non deve necessariamente essere uguale al numero di filiali in un livello diverso. Allo stesso modo, il numero di rami che risultano da un possibile risultato può variare anche all’interno dello stesso livello.

Esempio di albero

Ora che conosciamo la definizione e la teoria della creazione di un diagramma ad albero, esaminiamo passo dopo passo un esempio reale per comprendere meglio il concetto.

• Costruisci l’albero delle probabilità del lancio di tre monete indipendenti. Quindi determinare la probabilità che esca testa con tutti e tre i lanci.

Quando si sorteggiano, ci sono solo due risultati possibili, possiamo ottenere testa o croce. Pertanto, la probabilità di ottenere testa o croce lanciando una moneta è:

Una volta conosciute le probabilità dei possibili risultati, procediamo a rappresentare il diagramma ad albero.

Poiché i lanci delle monete sono indipendenti, la probabilità di ottenere testa o croce sarà sempre la stessa per ogni lancio. Pertanto, per costruire l’albero, è necessario rappresentare due rami (testa e croce) con la stessa probabilità per ogni lancio effettuato.

E una volta realizzato l’albero, tutto ciò che dobbiamo fare è determinare la probabilità di ottenere il lancio delle tre monete.

Pertanto in questo caso dobbiamo moltiplicare tutte le probabilità di ottenere testa, perché queste sono le probabilità del percorso che ci porta al risultato desiderato.

Pertanto, la probabilità che esca testa ai tre lanci della moneta viene calcolata come segue:

In breve, la probabilità di ottenere testa tre volte di seguito è del 12,5%.

Esercizio sull’albero risolto

In un villaggio ci sono solo 3 asili nido: il 60% dei bambini va all’asilo A, il 30% all’asilo B e il 10% all’asilo C. Inoltre, nei tre asili nido, il 55% delle persone sono bambine. Costruisci l’albero e calcola le seguenti probabilità:

• Probabilità che, quando un bambino viene selezionato a caso, sia una bambina dell’asilo nido B.
• Probabilità che quando un bambino viene selezionato casualmente da qualsiasi asilo nido, sarà un maschio.

Si noti che se la percentuale di ragazze in tutti gli asili nido è del 55%, la percentuale di ragazzi viene calcolata semplicemente sottraendo 1 meno 0,55:

Ora che conosciamo tutte le probabilità, possiamo creare l’albero delle probabilità con tutte le possibilità:

Pertanto, la probabilità di selezionare casualmente una ragazza dell’asilo nido B viene calcolata come segue:

D’altra parte, per determinare la probabilità di selezionare un ragazzo in ogni asilo nido, dobbiamo prima trovare la probabilità di selezionare un ragazzo per ogni asilo nido, quindi sommarli insieme:

Vantaggi della struttura ad albero

A causa delle caratteristiche della struttura ad albero, i vantaggi di questo tipo di grafico statistico sono i seguenti:

• I diagrammi ad albero sono molto utili per prendere decisioni.
• La relazione tra tutti i possibili risultati può essere rappresentata graficamente.
• È molto comodo trovare la causa principale di un problema.
• Rende più semplice risolvere problemi di probabilità e statistica.
• Un diagramma ad albero aiuta a organizzare le idee e ad analizzare la situazione.