Un'introduzione alla distribuzione esponenziale

La distribuzione esponenziale è una distribuzione di probabilità utilizzata per modellare il tempo che dobbiamo aspettare prima che si verifichi un determinato evento.

Questa distribuzione può essere utilizzata per rispondere a domande come:

• Quanto tempo dovrebbe attendere un rivenditore prima che un cliente entri nel suo negozio?
• Per quanto tempo un laptop continuerà a funzionare prima di rompersi?
• Per quanto tempo continuerà a funzionare la batteria di un’auto prima di scaricarsi?
• Quanto tempo dovremmo aspettare fino alla prossima eruzione vulcanica in una determinata regione?

In ogni scenario, vogliamo calcolare quanto tempo dovremo aspettare prima che si verifichi un determinato evento. Pertanto, ogni scenario potrebbe essere modellato utilizzando una distribuzione esponenziale.

Distribuzione esponenziale: PDF e CDF

Se una variabile casuale X segue una distribuzione esponenziale, allora la funzione di densità di probabilità di X può essere scritta:

f (x; λ) = λe ^-λx

Oro:

• λ: il parametro della velocità (calcolato come λ = 1/μ)
• e: Una costante pari a circa 2.718

La funzione di distribuzione cumulativa di

F (x; λ) = 1 – e ^-λx

In pratica, il CDF viene spesso utilizzato per calcolare le probabilità relative alla distribuzione esponenziale.

Ad esempio, supponiamo che il numero medio di minuti tra le eruzioni di un determinato geyser sia di 40 minuti. Quanto è probabile che dovremo aspettare meno di 50 minuti per un’eruzione?

Per risolvere questo problema, dobbiamo prima calcolare il parametro della velocità:

• λ = 1/μ
• λ = 1/40
• λ = 0,025

Possiamo inserire λ = 0,025 e x = 50 nella formula CDF:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 50) = 1 – e ^-0,025(50)
• P(X ≤ 50) = 0,7135

La probabilità che dovremo aspettare meno di 50 minuti per la prossima eruzione è 0,7135 .

Visualizza la distribuzione esponenziale

Il grafico seguente mostra la funzione di densità di probabilità di una variabile casuale

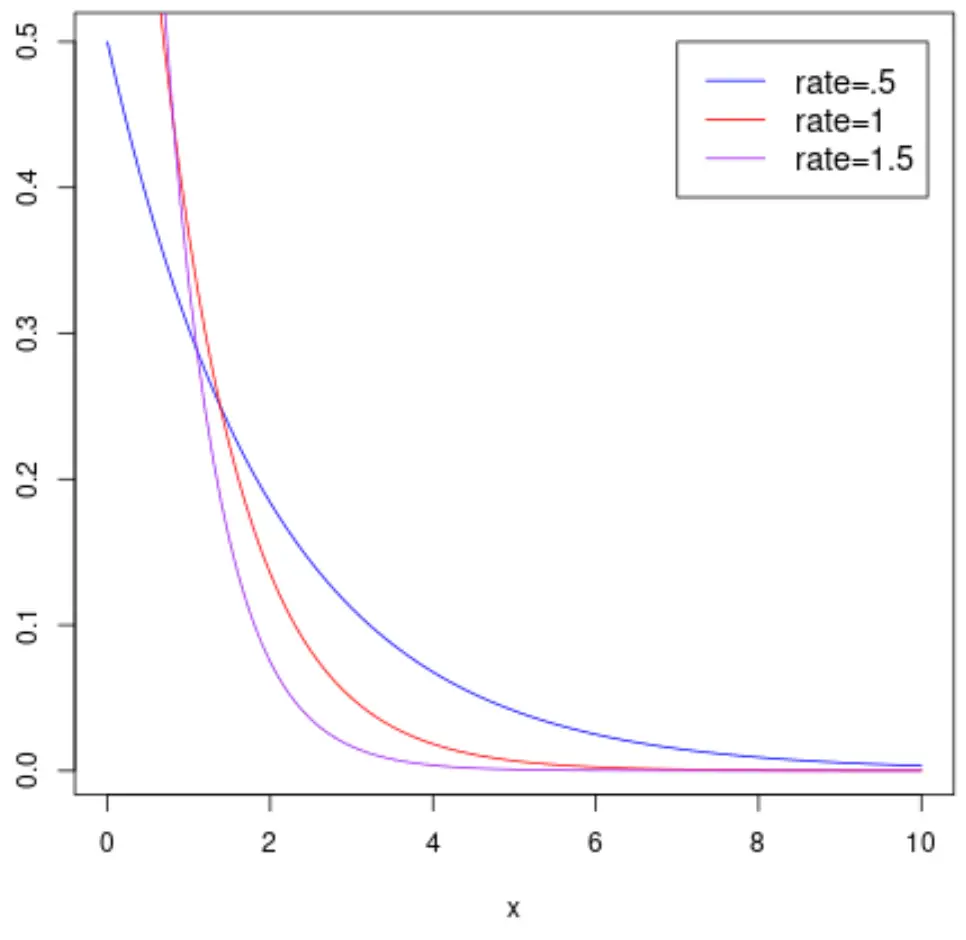
E il grafico seguente mostra la funzione di distribuzione cumulativa di una variabile casuale X che segue una distribuzione esponenziale con diversi parametri di velocità:

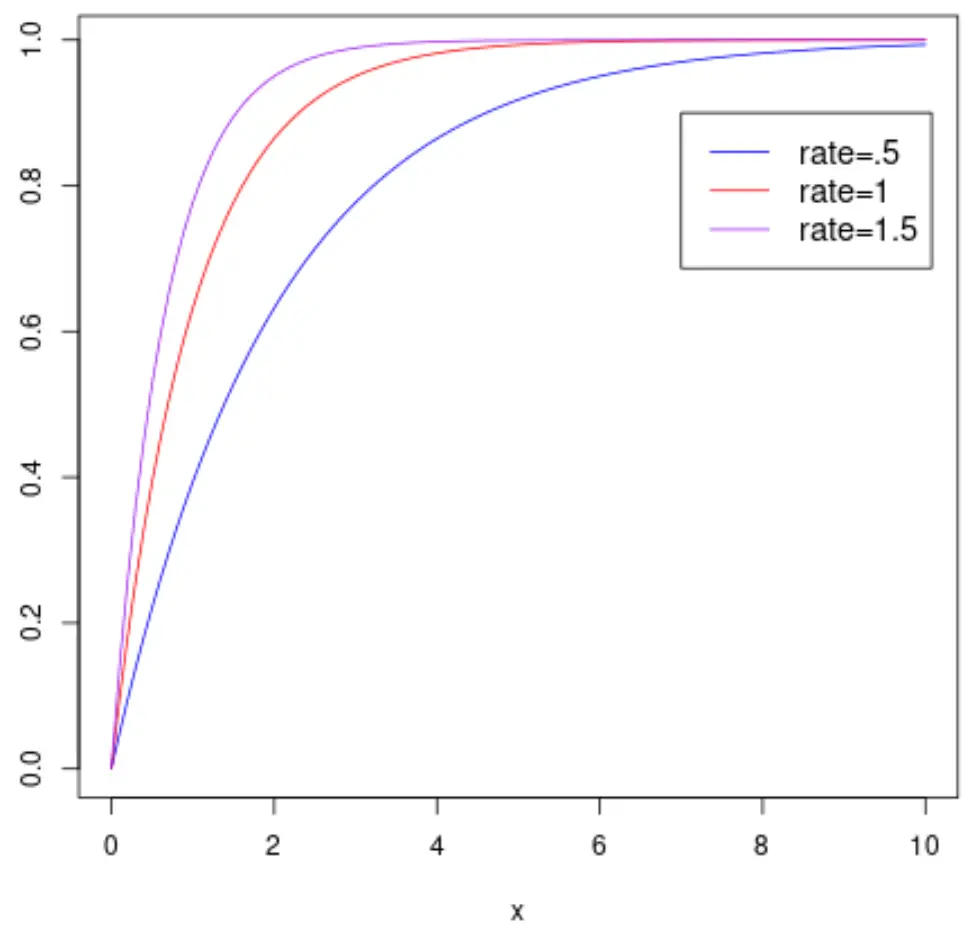
Nota: dai un’occhiata a questo tutorial per imparare come tracciare una distribuzione esponenziale in R.

Proprietà della distribuzione esponenziale

La distribuzione esponenziale ha le seguenti proprietà:

• Media: 1/λ
• Differenza: 1 / λ ²

Ad esempio, supponiamo che il numero medio di minuti tra le eruzioni di un determinato geyser sia di 40 minuti. Calcoleremo il tasso come λ = 1/μ = 1/40 = 0,025.

Potremmo quindi calcolare le seguenti proprietà per questa distribuzione:

• Tempo medio di attesa per la prossima eruzione: 1/λ = 1 /.025 = 40
• Variazione dei tempi di attesa per la prossima eruzione: 1/λ ² = 1 /.025 ² = 1600

Nota: la distribuzione esponenziale ha anche una proprietà senza memoria , ovvero la probabilità che si verifichi un evento futuro non è influenzata dal verificarsi di eventi passati.

Problemi pratici di distribuzione esponenziale

Utilizza i seguenti problemi pratici per verificare la tua conoscenza della distribuzione esponenziale.

Domanda 1: Un nuovo cliente entra in un negozio in media ogni due minuti. Dopo l’arrivo di un cliente, determinare la probabilità che un nuovo cliente arrivi in meno di un minuto.

Soluzione 1: il tempo medio tra i client è di due minuti. Pertanto il tasso può essere calcolato come segue:

• λ = 1/μ
• λ = 1/2
• λ = 0,5

Possiamo inserire λ = 0,5 e x = 1 nella formula CDF:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 1) = 1 – e ^-0,5(1)
• P(X ≤ 1) = 0,3935

La probabilità che dovremo aspettare meno di un minuto per l’arrivo del prossimo cliente è 0,3935 .

Domanda 2: In una determinata regione si verifica in media ogni 400 giorni un terremoto. Dopo un terremoto, determinare la probabilità che trascorrano più di 500 giorni prima che si verifichi il terremoto successivo.

Soluzione 2: Il tempo medio tra i terremoti è di 400 giorni. Pertanto il tasso può essere calcolato come segue:

• λ = 1/μ
• λ = 1/400
• λ = 0,0025

Possiamo inserire λ = 0,0025 e x = 500 nella formula CDF:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 1) = 1 – e ^-0,0025(500)
• P(X ≤ 1) = 0,7135

La probabilità che dovremo aspettare meno di 500 giorni per il prossimo terremoto è 0,7135. Quindi la probabilità che dovremo aspettare più di 500 giorni per il prossimo terremoto è 1 – 0,7135 = 0,2865 .

Domanda 3: Un call center riceve in media una nuova chiamata ogni 10 minuti. Dopo che un cliente ha chiamato, determina la probabilità che un nuovo cliente chiami entro 10-15 minuti.

Soluzione 3: il tempo medio tra le chiamate è di 10 minuti. Pertanto il tasso può essere calcolato come segue:

• λ = 1/μ
• λ = 1/10
• λ = 0,1

Possiamo utilizzare la seguente formula per calcolare la probabilità che un nuovo cliente chiami entro 10-15 minuti:

• P(10 < X ≤ 15) = (1 – e ^-0,1(15) ) – (1 – e ^-0,1(10) )
• P(10 < X ≤ 15) = 0,7769 – 0,6321
• P(10 < X ≤ 15) = 0,1448

La probabilità che un nuovo cliente chiami entro 10-15 minuti. è 0,1448 .

Risorse addizionali

Le seguenti esercitazioni forniscono introduzioni ad altre distribuzioni di probabilità comuni.

Un’introduzione alla distribuzione normale
Un’introduzione alla distribuzione binomiale
Un’introduzione alla distribuzione di Poisson
Un’introduzione alla distribuzione uniforme