Odds ratio aggiustato: definizione + esempi

In statistica, un odds ratio ci dice il rapporto tra la probabilità che un evento si verifichi in un gruppo di trattamento e la probabilità che un evento si verifichi in un gruppo di controllo.

I rapporti odd compaiono più comunemente nella regressione logistica , che è un metodo che utilizziamo per adattare un modello di regressione che ha una o più variabili predittive e una variabile di risposta binaria.

Un rapporto odd aggiustato è un rapporto odd che è stato aggiustato per altre variabili predittive in un modello.

È particolarmente utile per aiutarci a comprendere in che modo una variabile predittiva influisce sulle probabilità che si verifichi un evento, dopo aver adeguato l’effetto di altre variabili predittive.

L’esempio seguente illustra la differenza tra un rapporto odd e un rapporto odd modificato.

Esempio: calcolo dei rapporti di probabilità rettificati

Supponiamo di voler capire se l’età della madre influisce sulla probabilità di avere un bambino con basso peso alla nascita.

Per esplorare questo, possiamo eseguire una regressione logistica utilizzando l’età come variabile predittiva e il basso peso alla nascita (sì o no) come variabile di risposta .

Supponiamo di raccogliere dati su 300 madri e di adattare un modello di regressione logistica. Ecco i risultati:

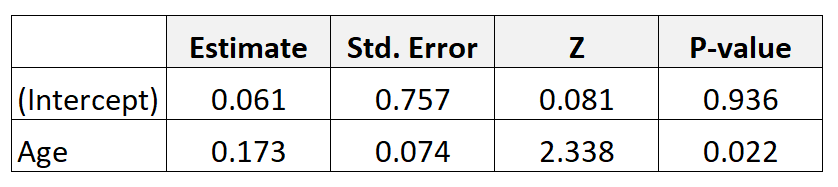
Per ottenere l’odds ratio per l’età è sufficiente esponenziare il coefficiente stimato dalla tabella: e ^0,173 = 1,189 .

Questo ci dice che un anno in più di età è associato ad un aumento di 1.189 probabilità che un bambino abbia un basso peso alla nascita. In altre parole, le probabilità di avere un bambino con basso peso alla nascita aumentano del 18,9% per ogni ulteriore aumento annuale dell’età.

Questo rapporto odd è chiamato rapporto odd “grezzo” o rapporto odd “non corretto” perché non è stato corretto per le altre variabili predittive nel modello poiché è l’ unica variabile predittiva nel modello.

Ma supponiamo di voler capire se l’età della madre e l’abitudine al fumo influiscono sulla probabilità di avere un bambino con basso peso alla nascita.

Per esplorare questo aspetto, possiamo eseguire una regressione logistica utilizzando l’età e il fumo (sì o no) come variabili predittive e il basso peso alla nascita come variabile di risposta .

Supponiamo di raccogliere dati su 300 madri e di adattare un modello di regressione logistica. Ecco i risultati:

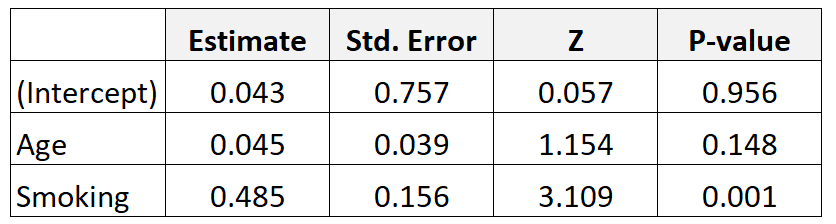
Ecco come interpretare i risultati:

Età: l’odds ratio corretto per l’età è calcolato come segue: e ^0,045 = 1,046 . Ciò significa che le probabilità di avere un bambino con basso peso alla nascita aumentano del 4,6% per ogni ulteriore aumento annuo di età, assumendo che la variabile fumo rimanga costante.

Ad esempio, supponiamo che la madre A e la madre B fumano entrambe. Se la madre A ha un anno in più della madre B, allora la probabilità che la madre A abbia un bambino con basso peso alla nascita è 1,046 volte la probabilità che la madre B abbia un bambino con basso peso alla nascita.

Fumare : l’odds ratio aggiustato per il fumo è calcolato come segue: ^e.485 = 1.624 . Ciò significa che le probabilità di avere un bambino con basso peso alla nascita aumentano del 62,4% se la madre fuma (rispetto a chi non fuma), assumendo che la variabile età rimanga costante.

Ad esempio, supponiamo che la madre A e la madre B abbiano entrambe 30 anni. Se la madre A fuma durante la gravidanza e la madre B non fuma, le probabilità che la madre A abbia un bambino con basso peso alla nascita sono superiori del 62,4% rispetto alle probabilità che la madre B abbia un bambino con basso peso alla nascita.

Si noti che il rapporto odd corretto per l’età è inferiore al rapporto odd non corretto dell’esempio precedente. Questo perché quando altre variabili predittive aumentano le probabilità che si verifichi la variabile di risposta, l’odds ratio corretto per una variabile predittiva già presente nel modello diminuirà sempre.

Riepilogo: rapporto di probabilità rispetto al rapporto di probabilità corretto

Un rapporto di probabilità (a volte chiamato rapporto di probabilità “grezzo”) è utile per dirci come i cambiamenti in una variabile predittrice influenzano le possibilità che si verifichi una variabile di risposta.

Un rapporto odd corretto è utile per dirci in che modo i cambiamenti in una variabile predittiva influenzano le probabilità che si verifichi una variabile di risposta, dopo aver controllato altre variabili predittive in un modello.

Risorse addizionali

Introduzione alla regressione logistica
Come eseguire la regressione logistica in R
Come eseguire la regressione logistica in Python