Cos'è una relazione monotona? (definizione + esempi)
In statistica, una relazione monotona tra due variabili si riferisce a uno scenario in cui un cambiamento in una variabile è solitamente associato a un cambiamento in una direzione specifica in un’altra variabile.
Esistono due tipi di relazioni monotone:
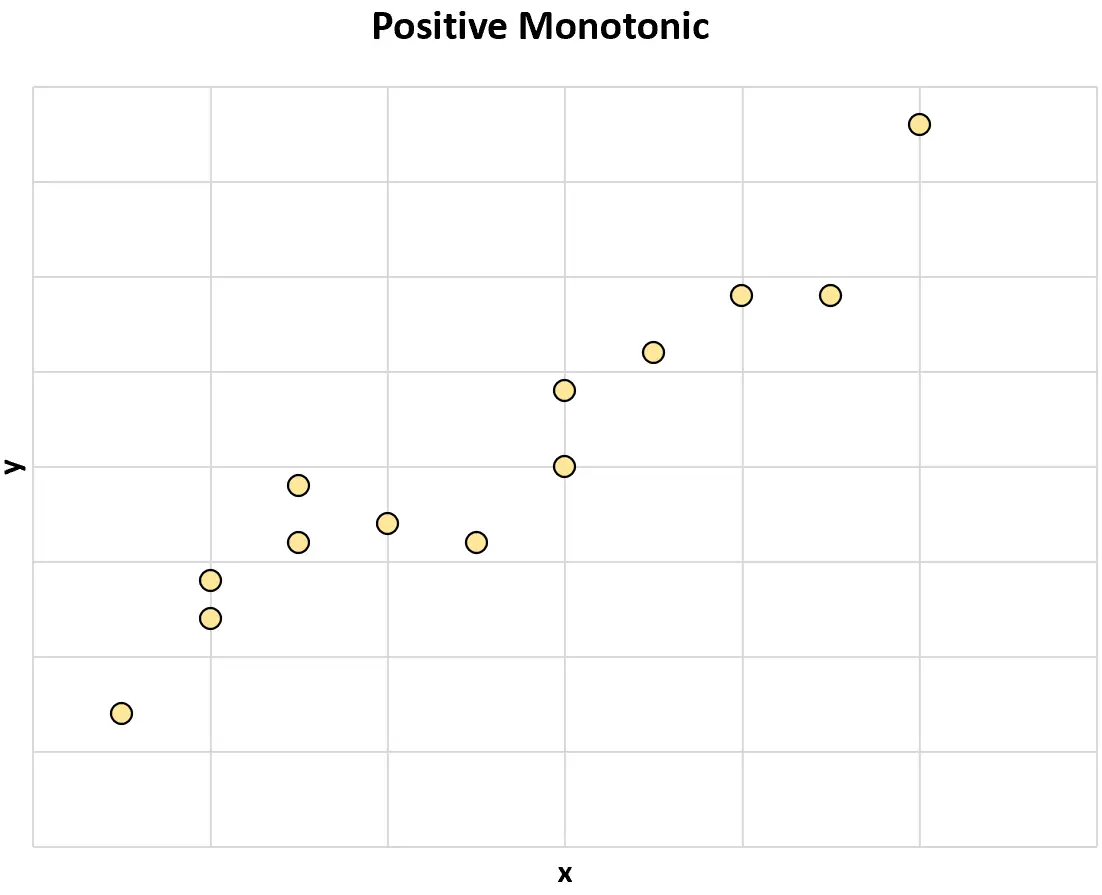
Monotonico positivo: quando il valore di una variabile aumenta, anche il valore dell’altra variabile tende ad aumentare.
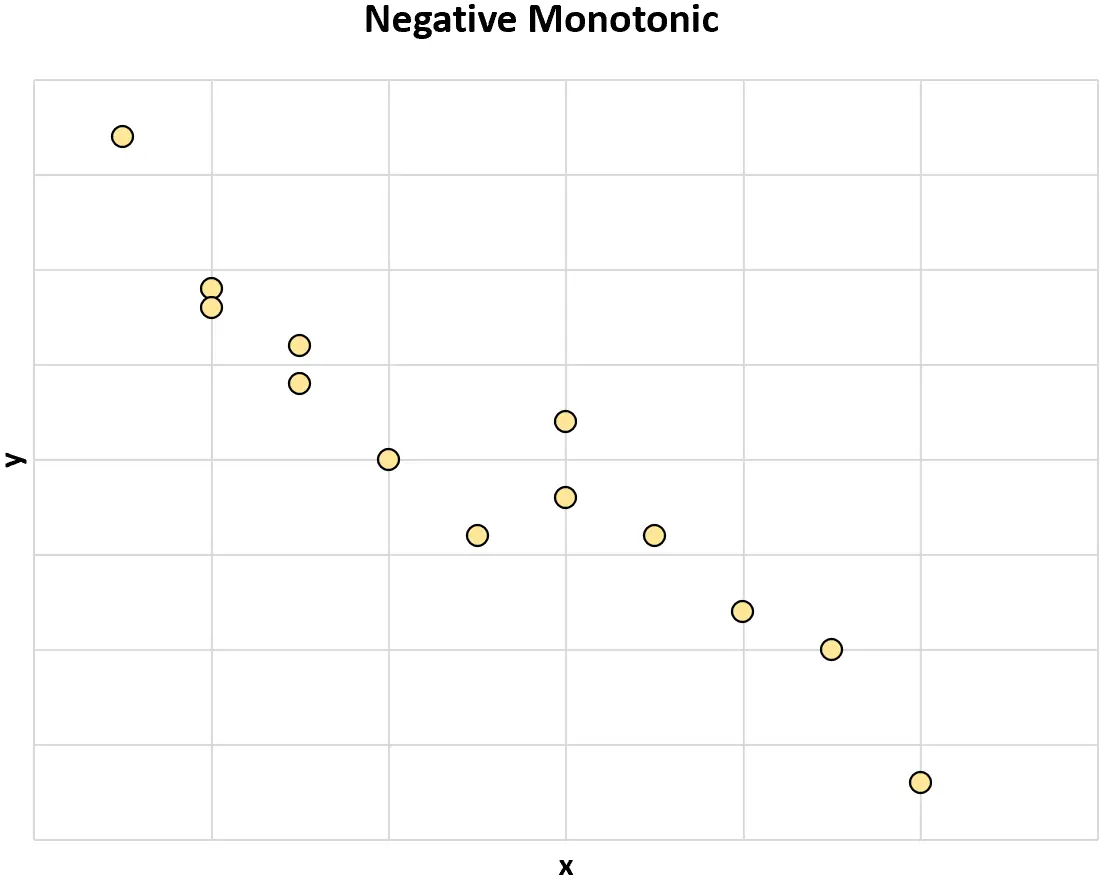
Monotonico negativo: quando il valore di una variabile aumenta, il valore dell’altra variabile tende a diminuire.
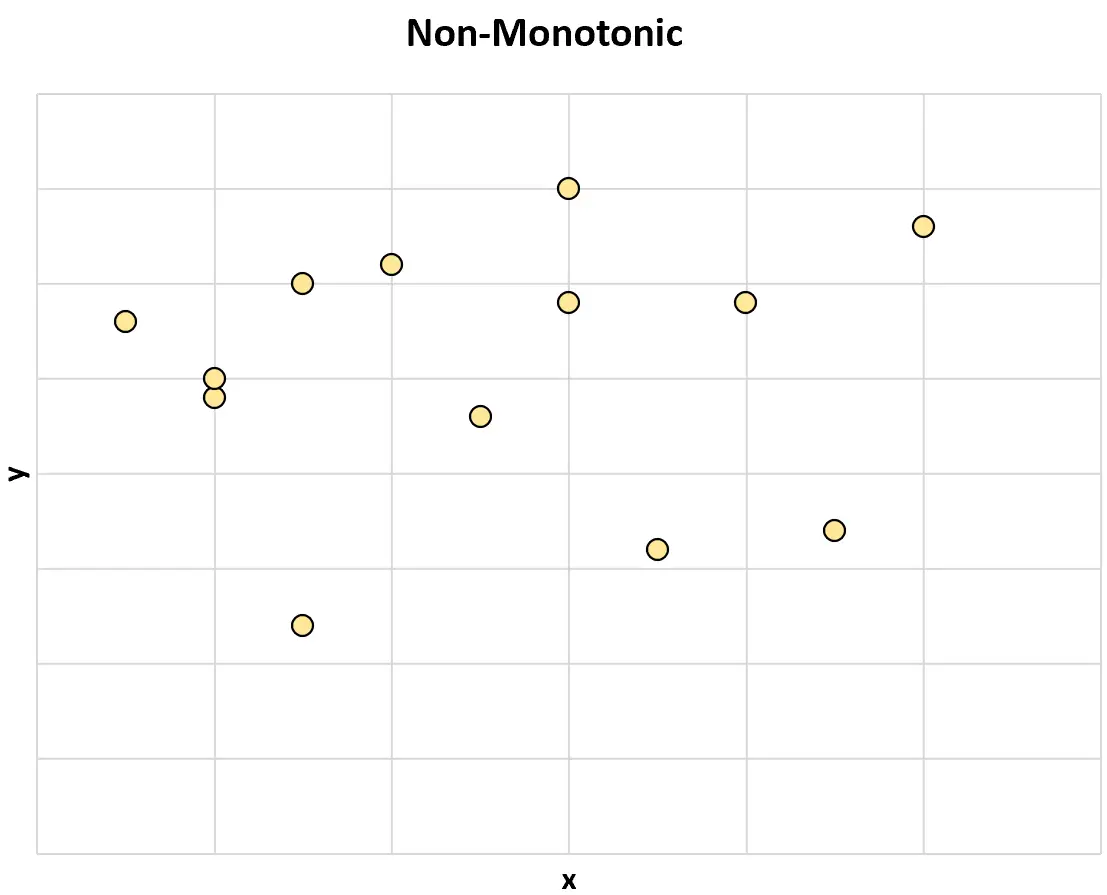
Se due variabili generalmente non cambiano nella stessa direzione, si dice che abbiano una relazione non monotona .
Ecco un esempio di relazione non monotona tra due variabili:
Ed ecco un altro esempio di relazione non monotona tra due variabili:
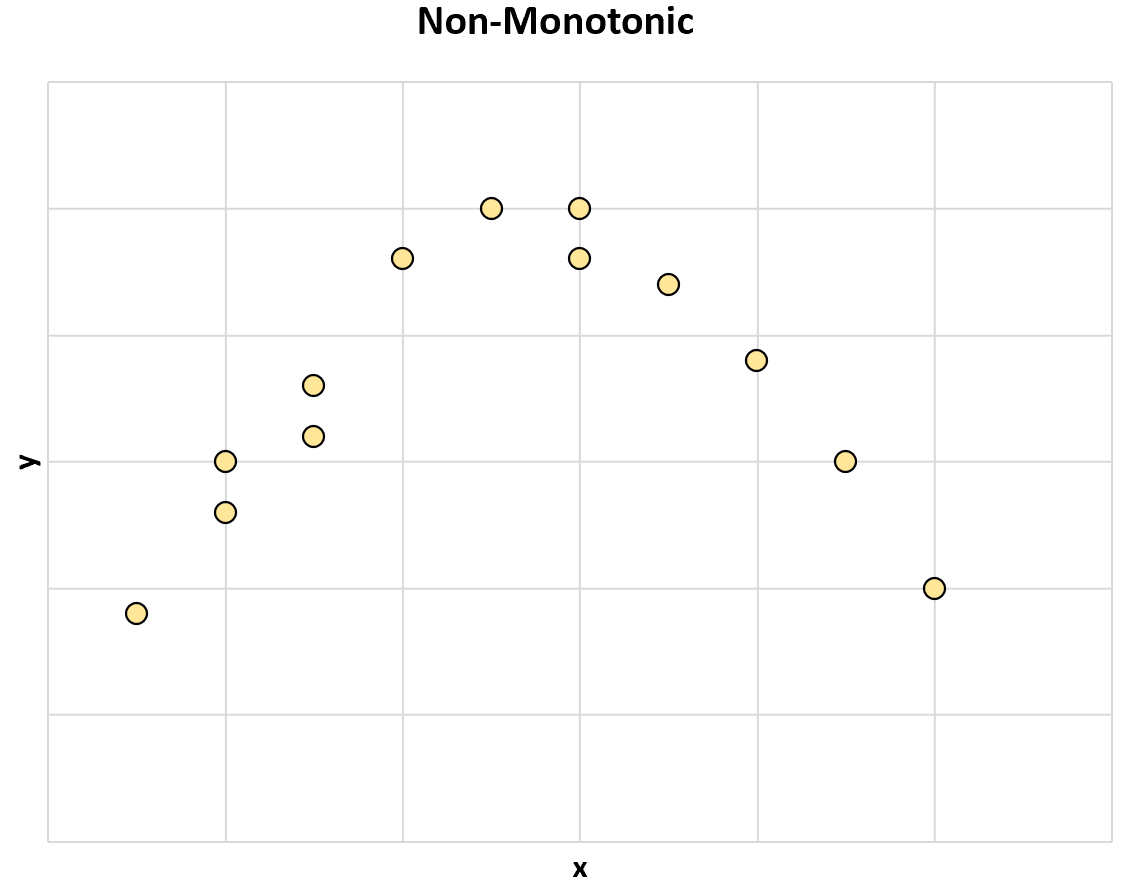
All’aumentare del valore di x, il valore di y a volte aumenta, ma a volte il valore di y diminuisce .
Rigorosamente monotono o non strettamente monotono
Si dice che due variabili hanno una relazione strettamente monotona se i cambiamenti in una variabile sono sempre associati a cambiamenti nella stessa direzione in un’altra variabile.
Ad esempio, il grafico seguente illustra una relazione monotona strettamente positiva tra due variabili:
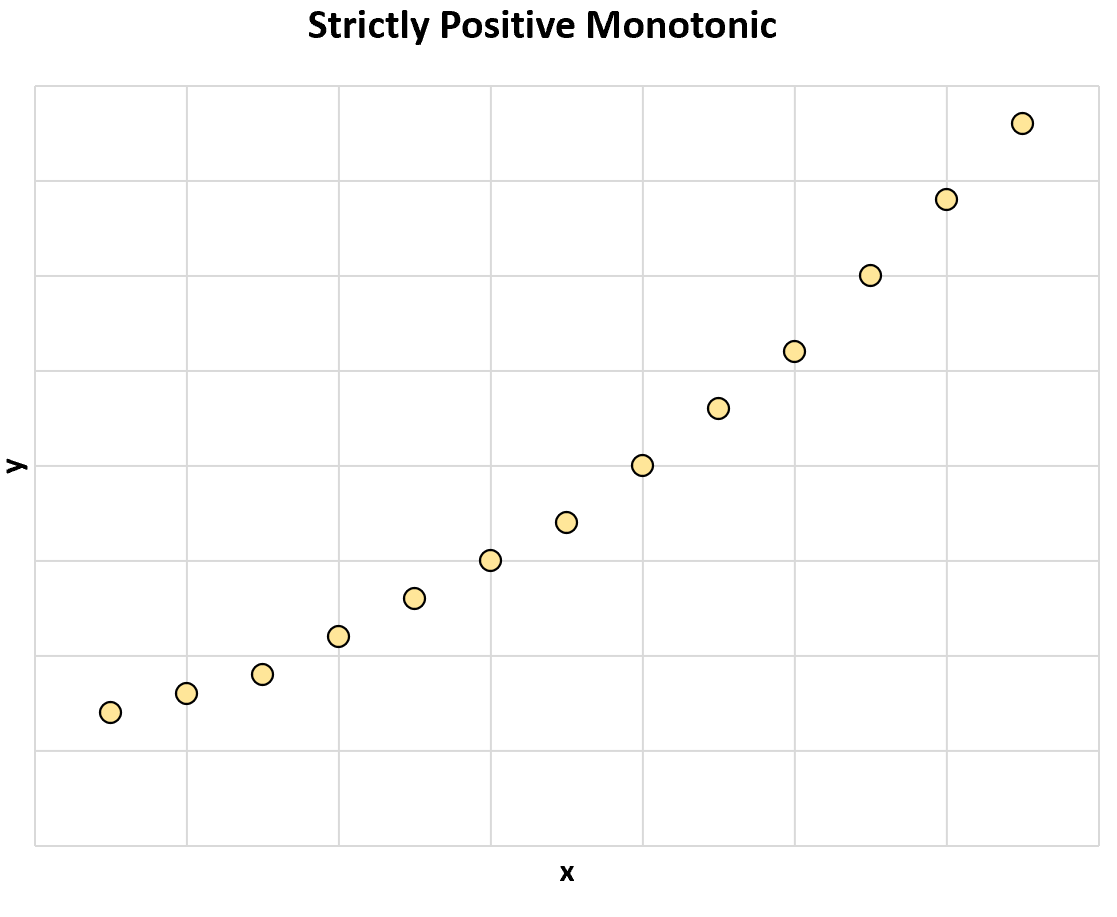
All’aumentare del valore di x, aumenta sempre il valore di y.
Il grafico seguente illustra una relazione monotona strettamente negativa tra due variabili:
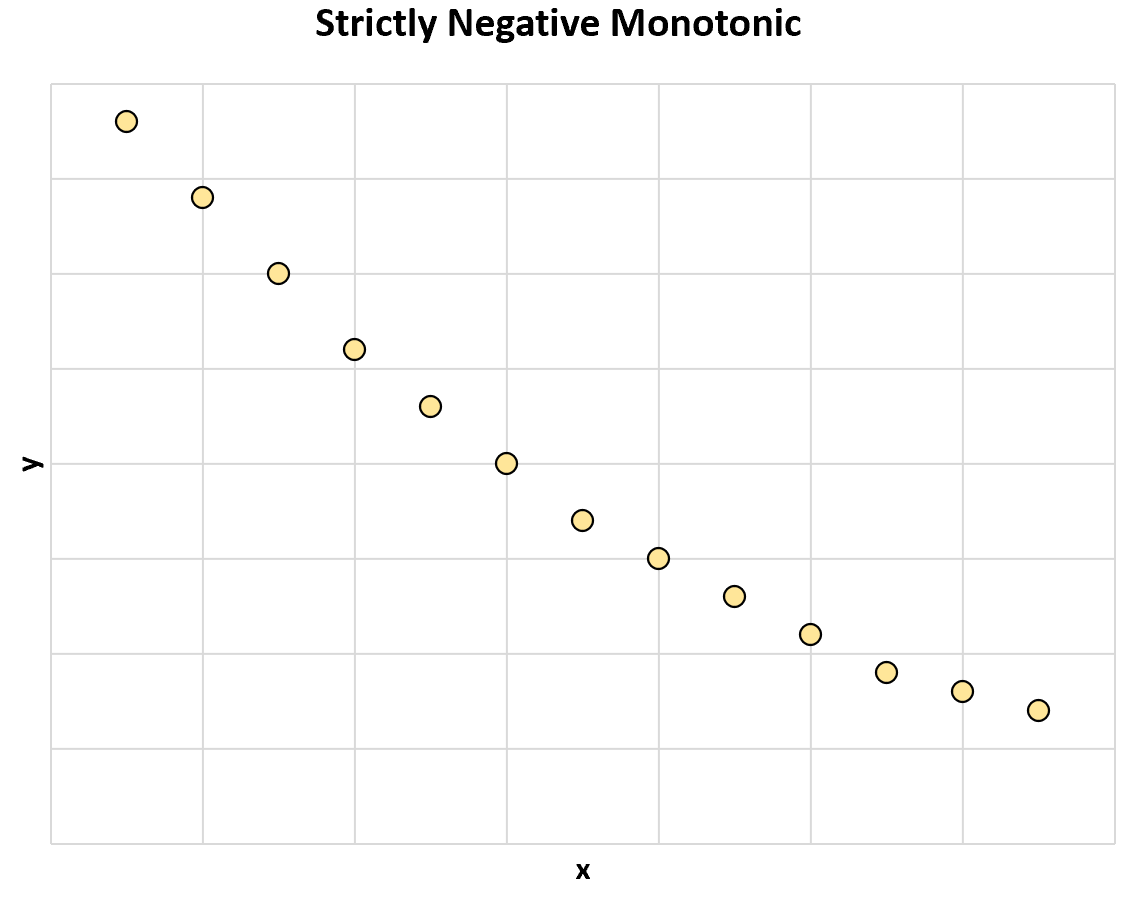
All’aumentare del valore di x, il valore di y diminuisce sempre .
Come quantificare le relazioni monotone
Il modo più comune per quantificare la relazione tra due variabili è utilizzare il coefficiente di correlazione di Pearson , che misura l’associazione lineare tra due variabili.
Questo coefficiente assume sempre un valore compreso tra -1 e 1 dove:
- -1 indica una correlazione lineare perfettamente negativa tra due variabili
- 0 indica alcuna correlazione lineare tra due variabili
- 1 indica una correlazione lineare perfettamente positiva tra due variabili
Quanto più il coefficiente è vicino a 1, tanto più forte è la relazione positiva tra due variabili. Al contrario, più il coefficiente è vicino a -1, più forte è la relazione negativa tra due variabili.
Tuttavia, se la relazione tra due variabili è monotona ma non lineare (come una relazione esponenziale), allora è una buona idea utilizzare la correlazione Spearman Rank , che è stata progettata per gestire bene le relazioni monotone.
Indipendentemente dal tipo di coefficiente di correlazione che stai calcolando, è sempre una buona idea creare un grafico a dispersione per visualizzare anche la relazione tra le variabili.