Cosa significa se una statistica è resiliente?
Una statistica si dice resiliente se non è sensibile a valori estremi.
Ecco due esempi di statistiche resilienti:
- La mediana
- Lo spazio interquartile
Ecco alcuni esempi di statistiche che non reggono :
- La media
- La deviazione standard
- Ordinato
L’esempio seguente illustra la differenza tra statistiche resilienti e non resistenti.
Esempio: statistiche resistenti e non resistenti
Supponiamo di avere il seguente set di dati:
Set di dati: 2, 5, 6, 7, 8, 13, 15, 18, 22, 24, 29
Utilizzando una calcolatrice o un software statistico, possiamo calcolare il valore delle seguenti statistiche di detenzione per questo set di dati:
- Media: 13
- Intervallo interquartile: 13,5
Possiamo anche calcolare il valore delle seguenti statistiche non resilienti per questo set di dati:
- Media: 13,54
- Deviazione standard: 8,82
- Portata: 27
Consideriamo ora se a questo set di dati fosse stato aggiunto un valore anomalo estremo:
Set di dati: 2, 5, 6, 7, 8, 13, 15, 18, 22, 24, 29, 450
Possiamo nuovamente calcolare il valore delle seguenti statistiche resilienti per questo set di dati:
- Media: 14
- Intervallo interquartile: 15,75
Possiamo anche calcolare il valore delle seguenti statistiche non resilienti per questo set di dati:
- Media: 49,92
- Deviazione standard: 126,27
- Gamma: 448
Notate quanto sono cambiate le statistiche di non resistenza semplicemente aggiungendo un valore estremo al set di dati:
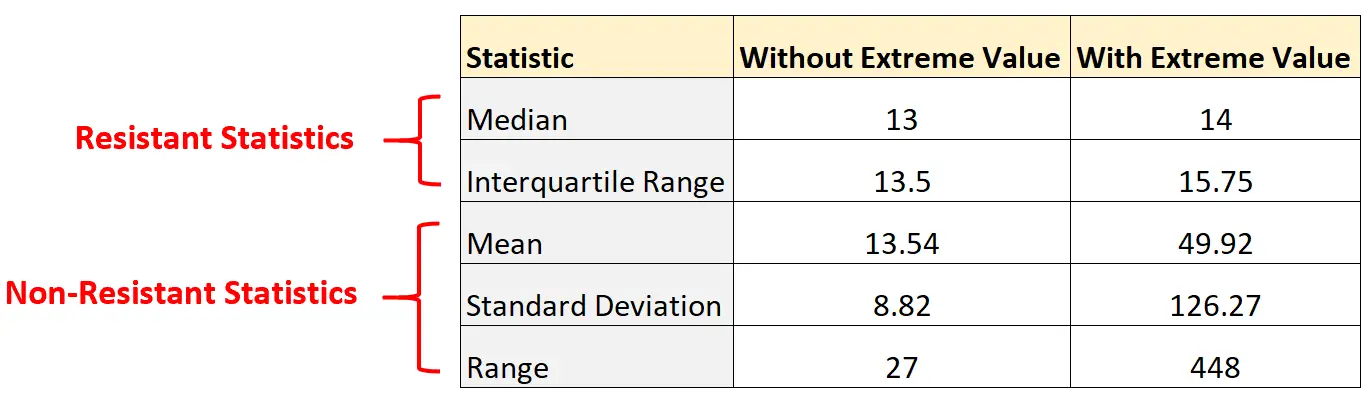
Al contrario, le statistiche dei combattenti della resistenza non sono cambiate di molto. La mediana e l’intervallo interquartile sono cambiati solo leggermente.
Quando utilizzare le statistiche resilienti
Le statistiche più comunemente utilizzate per misurare il centro e la dispersione dei valori in un set di dati sono rispettivamente la media e la deviazione standard.
Sfortunatamente, entrambe queste statistiche sono sensibili a valori estremi. Pertanto, se in un set di dati sono presenti valori anomali, la media e la deviazione standard non descriveranno accuratamente la distribuzione dei valori in un set di dati.
Si consiglia invece di utilizzare la mediana e l’intervallo interquartile per misurare il centro e la dispersione dei valori in un set di dati se sono presenti valori anomali, poiché entrambe queste statistiche sono robuste .
Risorse addizionali
In che modo i valori anomali influenzano la media?
Quando utilizzare la media rispetto alla mediana
Quando utilizzare l’intervallo interquartile rispetto alla deviazione standard