Come utilizzare la distribuzione esponenziale in excel

La distribuzione esponenziale è una distribuzione di probabilità utilizzata per modellare il tempo che dobbiamo aspettare prima che si verifichi un determinato evento.

Questa distribuzione può essere utilizzata per rispondere a domande come:

• Quanto tempo dovrebbe attendere un rivenditore prima che un cliente entri nel suo negozio?
• Per quanto tempo una batteria continuerà a funzionare prima di scaricarsi?
• Per quanto tempo un computer continuerà a funzionare prima di rompersi?

In ogni scenario, vogliamo calcolare quanto tempo dovremo aspettare prima che si verifichi un determinato evento. Pertanto, ogni scenario potrebbe essere modellato utilizzando una distribuzione esponenziale.

Se una variabile casuale X segue una distribuzione esponenziale, allora la funzione di densità cumulativa di X può essere scritta:

F (x; λ) = 1 – e ^-λx

Oro:

• λ: il parametro della velocità (calcolato come λ = 1/μ)
• e: Una costante pari a circa 2.718

Per calcolare le probabilità relative alla funzione di densità cumulativa della distribuzione esponenziale in Excel, possiamo utilizzare la seguente formula:

 =EXPON.DIST(x, lambda, cumulative)

Oro:

• x : il valore della variabile casuale distribuita esponenzialmente
• lambda : il parametro della velocità
• cumulativo : se utilizzare o meno la funzione di densità cumulativa (VERO o FALSO)

Gli esempi seguenti mostrano come utilizzare questa formula nella pratica.

Esempio 1: tempo fino all’arrivo del cliente successivo

In media un nuovo cliente entra in un negozio ogni due minuti. Dopo l’arrivo di un cliente, determinare la probabilità che un nuovo cliente arrivi in meno di un minuto.

Soluzione: il tempo medio tra i clienti è di due minuti. Pertanto il tasso può essere calcolato come segue:

• λ = 1/μ
• λ = 1/2
• λ = 0,5

Possiamo quindi utilizzare la seguente formula di Excel per calcolare la probabilità che un nuovo cliente arrivi in meno di un minuto:

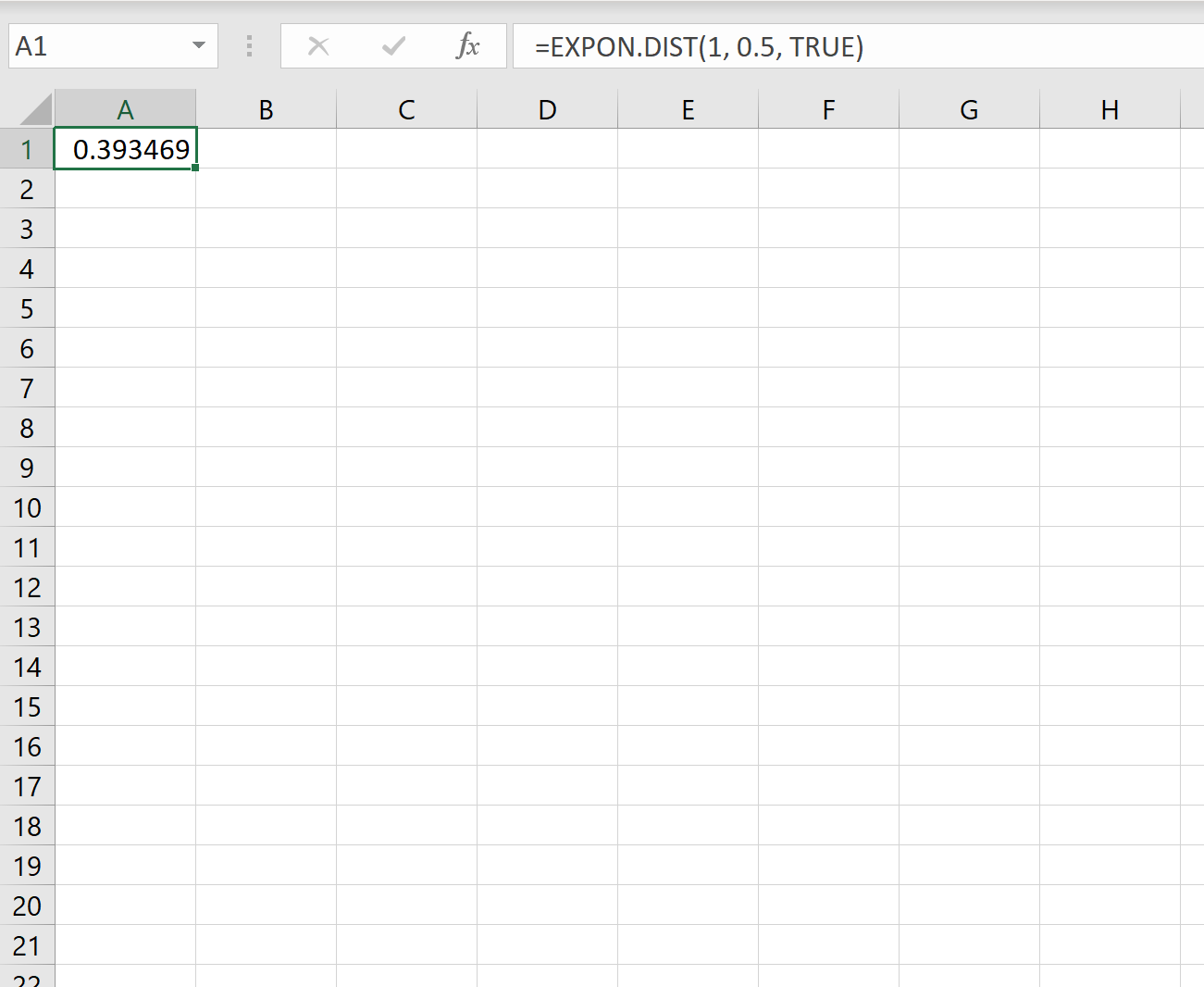
La probabilità che dovremo aspettare meno di un minuto per l’arrivo del prossimo cliente è 0,393469 .

Esempio 2: Tempo al prossimo terremoto

Supponiamo che in una determinata regione si verifichi un terremoto in media ogni 400 giorni. Dopo un terremoto, determinare la probabilità che trascorrano più di 500 giorni prima che si verifichi il terremoto successivo.

Soluzione: Il tempo medio tra i terremoti è di 400 giorni. Pertanto il tasso può essere calcolato come segue:

• λ = 1/μ
• λ = 1/400
• λ = 0,0025

Quindi, possiamo utilizzare la seguente formula in Excel per calcolare la probabilità che il prossimo terremoto impiegherà meno di 500 giorni a verificarsi:

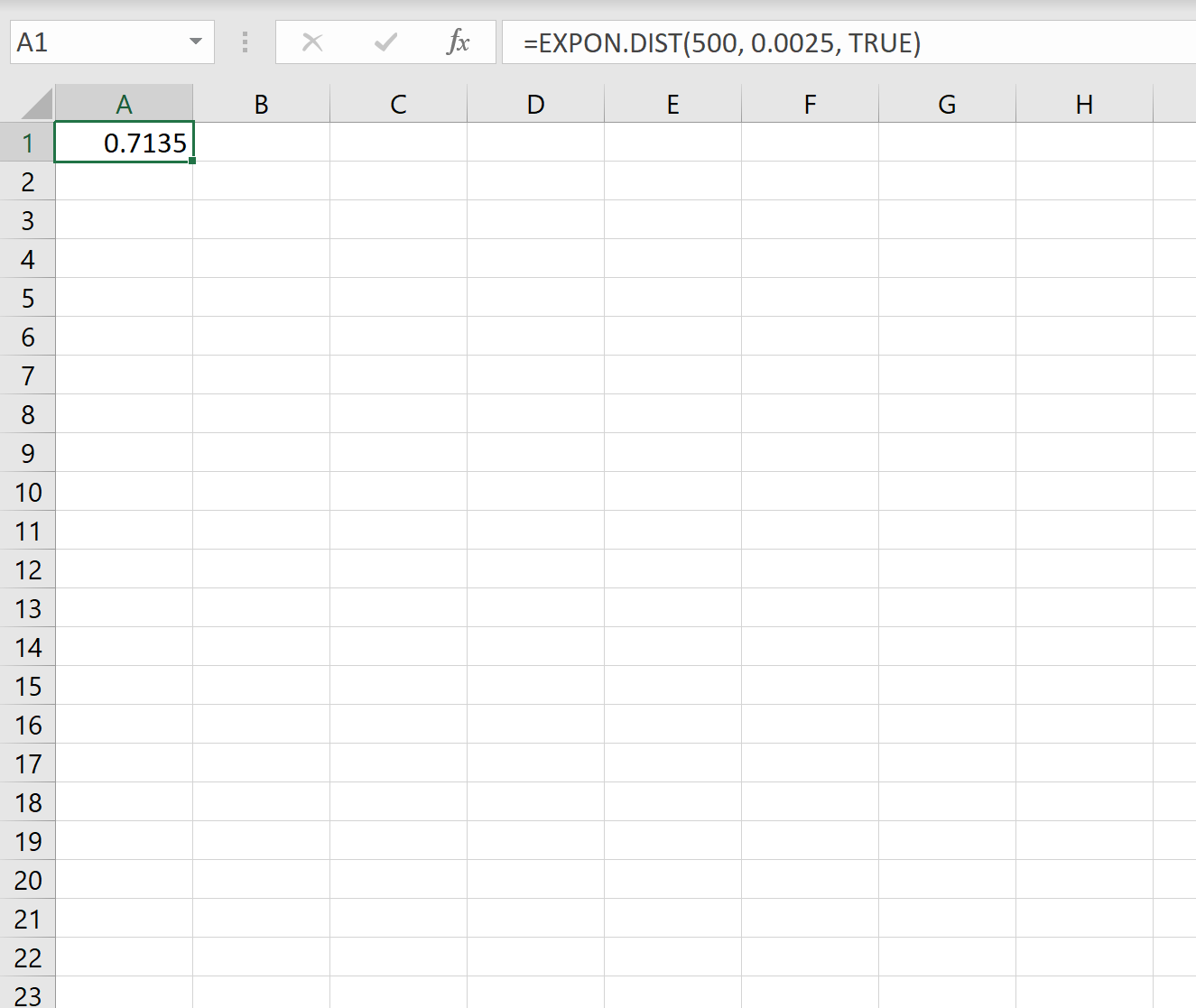
La probabilità che manchino meno di 500 giorni al prossimo terremoto è 0,7135.

Quindi la probabilità che dovremo aspettare più di 500 giorni per il prossimo terremoto è 1 – 0,7135 = 0,2865 .

Esempio 3: Tempo fino alla prossima telefonata

Supponiamo che un call center riceva in media una nuova chiamata ogni 10 minuti. Dopo che un cliente ha chiamato, determina la probabilità che un nuovo cliente chiami entro 10-15 minuti.

Soluzione: il tempo medio tra le chiamate è di 10 minuti. Pertanto il tasso può essere calcolato come segue:

• λ = 1/μ
• λ = 1/10
• λ = 0,1

Quindi, possiamo utilizzare la seguente formula in Excel per calcolare la probabilità che il prossimo cliente chiami entro 10-15 minuti:

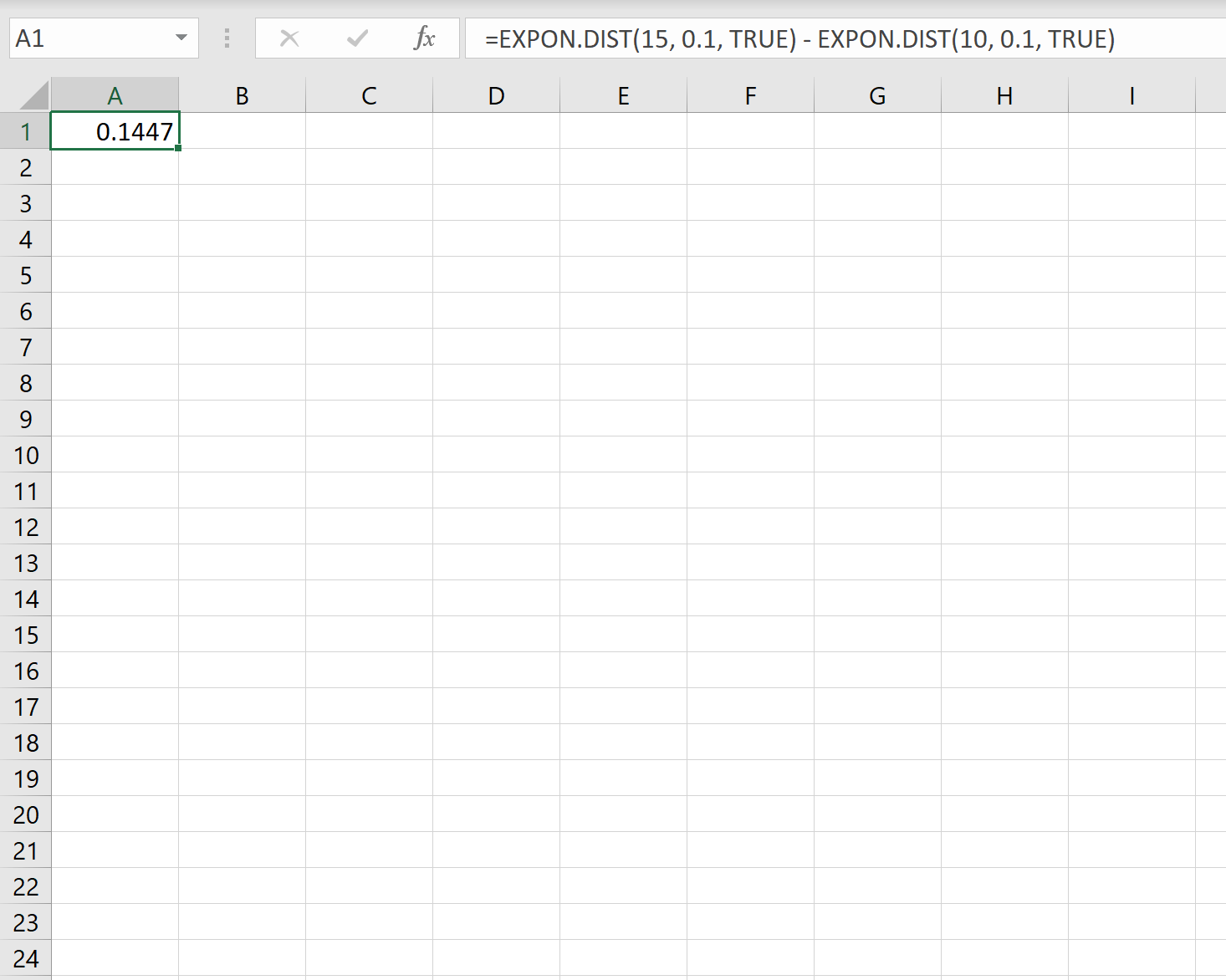
La probabilità che un nuovo cliente chiami entro 10-15 minuti. è 0,1447 .

Risorse addizionali

Un’introduzione alla distribuzione esponenziale
La proprietà senza memoria della distribuzione esponenziale
Come tracciare una distribuzione esponenziale in R