Distribuzione di frequenza

Questo articolo spiega cosa sono le distribuzioni di frequenza e come vengono ottenute. Troverai anche esempi passo passo di distribuzioni di frequenza e, inoltre, potrai esercitarti con esercizi risolti.

Cos’è una distribuzione di frequenza?

In statistica, la distribuzione di frequenza è una tabella in cui i diversi valori di un campione sono raggruppati in righe e in ciascuna colonna viene visualizzato un tipo di frequenza di ciascun valore. Pertanto, la distribuzione di frequenza viene utilizzata per mostrare tutti i tipi di frequenze in un set di dati.

Più specificamente, una distribuzione di frequenza include frequenza assoluta, frequenza assoluta cumulativa, frequenza relativa e frequenza relativa cumulativa.

Una delle caratteristiche delle distribuzioni di frequenza è che sono molto utili per riassumere un campione statistico di una variabile quantitativa e di una variabile qualitativa.

Come realizzare una distribuzione di frequenza

Per eseguire una distribuzione di frequenza, è necessario seguire i seguenti passaggi:

1. Organizza i dati in diverse categorie e crea una tabella in cui ogni riga corrisponde a una categoria.
2. Calcola la frequenza assoluta di ciascuna categoria nella seconda colonna della tabella.
3. Calcola la frequenza assoluta cumulativa di ciascuna categoria nella terza colonna della tabella.
4. Calcola la frequenza relativa di ciascuna categoria nella quarta colonna della tabella.
5. Calcolare la frequenza relativa cumulativa di ciascuna categoria nella quinta colonna della tabella.
6. Facoltativamente, è possibile aggiungere due colonne in cui la frequenza relativa e la frequenza relativa cumulativa vengono calcolate in percentuale, per questo è sufficiente moltiplicare entrambe le colonne per 100.

Esempio di distribuzione di frequenza

Una volta vista la definizione di distribuzione di frequenza e la teoria su come è costruita, in questa sezione viene risolto passo dopo passo un esempio.

• I voti ottenuti in materia di statistica in una classe di 30 studenti sono i seguenti. Costruire una distribuzione di frequenza del set di dati.

Poiché tutti i numeri possono essere solo numeri interi, è una variabile discreta. Non è quindi necessario raggruppare i dati in intervalli.

Quindi, per creare una distribuzione di frequenza, dobbiamo costruire una tabella in cui ogni valore diverso sarà una riga, quindi dobbiamo trovare la frequenza assoluta di ciascun valore:

Si noti che la somma di tutte le frequenze assolute è uguale al numero totale di dati. Se questa regola non viene rispettata significa che hai dimenticato di fornire alcuni dati.

Ora che conosciamo la frequenza assoluta, dobbiamo calcolare la frequenza assoluta cumulativa. Per questo calcolo abbiamo due opzioni: o aggiungiamo la frequenza assoluta del valore più tutte le frequenze assolute dei valori più piccoli, oppure, al contrario, aggiungiamo la frequenza assoluta del valore più la frequenza assoluta cumulativa del valore precedente.

La frequenza assoluta cumulativa dell’ultimo valore corrisponde sempre al numero totale di dati, puoi utilizzare questo trucco per verificare che i calcoli siano corretti.

Successivamente, dobbiamo determinare la frequenza relativa, che viene calcolata dividendo la frequenza assoluta per il numero totale di punti dati (30):

Tieni presente che la somma di tutte le frequenze relative è sempre uguale a 1, altrimenti significa che un certo calcolo della distribuzione di frequenza è sbagliato.

Infine, dobbiamo solo estrarre la frequenza relativa cumulativa. Per fare ciò, è necessario aggiungere la frequenza relativa del valore in questione più tutte le frequenze relative precedenti o, che è la stessa cosa, la frequenza relativa accumulata precedente:

In breve, la distribuzione di frequenza con tutte le frequenze dei dati problematici è la seguente:

Distribuzione di frequenza per dati raggruppati

Per creare una distribuzione di frequenza per dati raggruppati in intervalli , l’unica differenza è che il set di dati deve prima essere raggruppato in intervalli diversi, ma il resto dei calcoli viene eseguito allo stesso modo di una distribuzione di frequenza senza raggruppare i dati.

Ad esempio, di seguito viene risolto il problema di costruire una distribuzione di frequenza per dati raggruppati.

• È stata misurata l’altezza di 20 persone e sono stati ottenuti i risultati riportati di seguito. Creare una distribuzione di frequenza separando i dati in intervalli.

I dati in questo esempio seguono una distribuzione continua, poiché i numeri possono essere decimali e quindi possono assumere qualsiasi valore. Pertanto, creeremo la distribuzione di frequenza raggruppando i dati in intervalli.

Sebbene esistano diverse regole matematiche per creare gli intervalli di un campione, in questo caso creeremo semplicemente intervalli con una larghezza di 10 decimi.

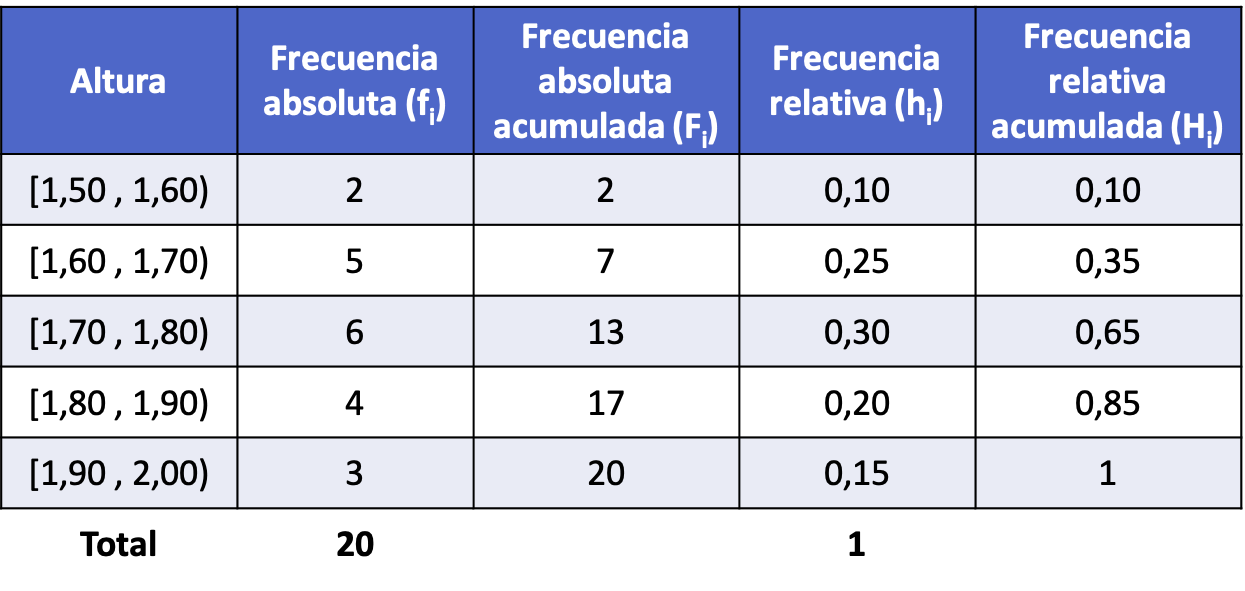
Quindi, dopo aver calcolato tutti i tipi di frequenza per ciascun intervallo (la procedura è la stessa dell’esempio sopra), la distribuzione della frequenza con i dati raggruppati in intervalli è la seguente:

Esercizi sulla distribuzione della frequenza risolti

Esercizio 1

Abbiamo chiesto a 20 persone quante volte vanno al cinema al mese ed ecco i risultati:

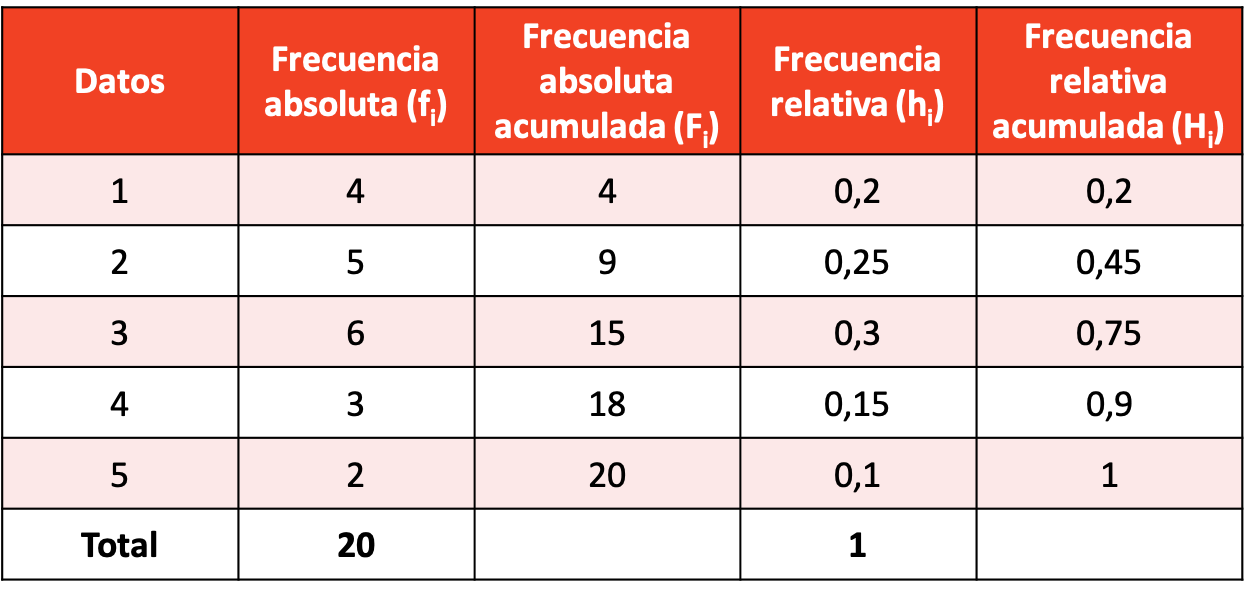
Crea una distribuzione di frequenza con il campione di dati risultante.

La distribuzione di frequenza con calcoli di tutti i tipi di frequenze è la seguente:

Esercizio 2

Vorresti realizzare uno studio statistico sul peso dei lavoratori in un’azienda con 36 dipendenti. Ecco i pesi dei lavoratori espressi in chilogrammi:

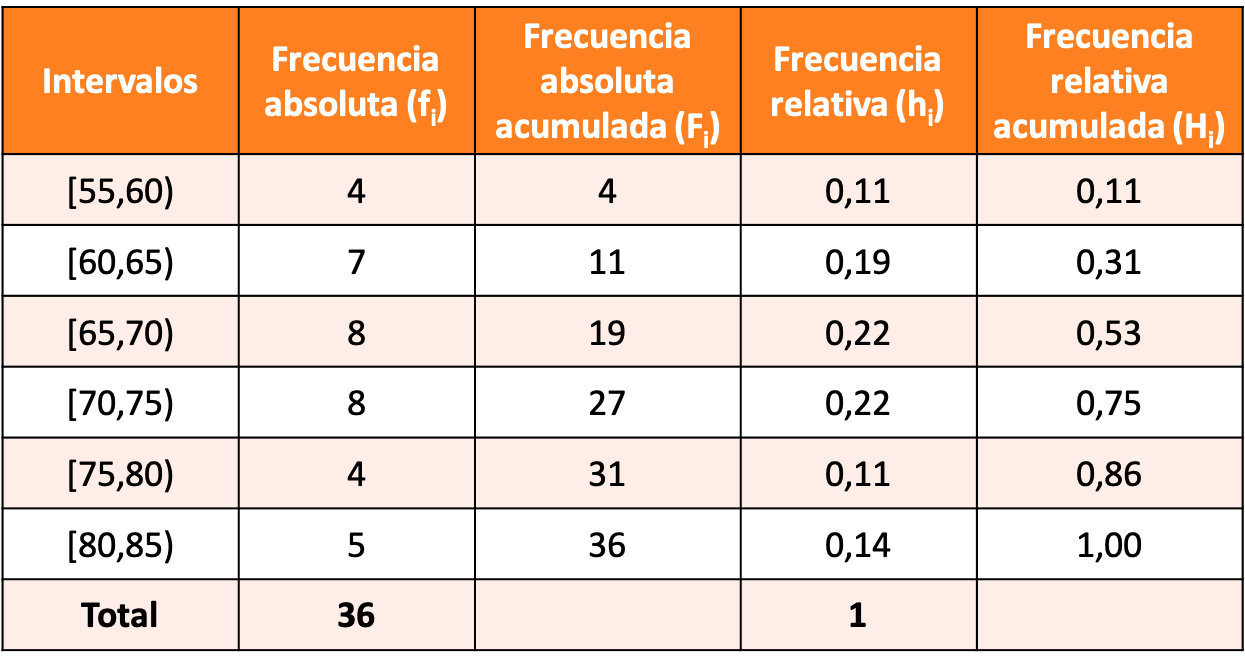
Costruisci una distribuzione di frequenza con dati raggruppati creando intervalli di 5 unità e lascia che il primo intervallo sia [55,60).

La soluzione dell’esercizio è la seguente distribuzione di frequenza: