Perché la deviazione standard è importante? (spiegazione + esempi)
La deviazione standard viene utilizzata per misurare la distribuzione dei valori in un campione.
Possiamo utilizzare la seguente formula per calcolare la deviazione standard di un dato campione:
√ Σ(x i – x bar ) 2 / (n-1)
Oro:
- Σ: Un simbolo che significa “somma”
- x i : l’i -esimo valore del campione
- x bar : Il campione significa
- n: la dimensione del campione
Quanto più alto è il valore della deviazione standard, tanto più dispersi sono i valori in un campione. Al contrario, più basso è il valore della deviazione standard, più i valori sono raggruppati.
Una domanda che spesso gli studenti si pongono è: perché la deviazione standard è importante?
La risposta: la deviazione standard è importante perché ci dice la distribuzione dei valori in un dato set di dati.
analizziamo un set di dati Ogni volta, vogliamo trovare le seguenti metriche:
- Il centro del set di dati . Il modo più comune per misurare il “centro” è utilizzare la media e la mediana.
- La distribuzione dei valori nel set di dati . Il modo più comune per misurare lo spread è utilizzare la deviazione standard.
Sapendo dove si trova il centro e qual è la distribuzione dei valori, possiamo comprendere bene la distribuzione dei valori in qualsiasi set di dati.
I seguenti esempi illustrano l’importanza della deviazione standard nella pratica.
Esempio 1: distribuzione degli stipendi
Supponiamo che lo stipendio medio presso l’azienda A sia di $ 80.000 e che la deviazione standard sia di $ 20.000. Poiché la deviazione standard è così ampia, non vi è alcuna garanzia che verrai pagato vicino a $ 80.000 all’anno se lavori in questa azienda perché esiste una tale variazione negli stipendi.
Al contrario, supponiamo che anche lo stipendio medio presso la società B sia di $ 80.000, ma la deviazione standard sia solo di $ 4.000. Poiché questa deviazione standard è così piccola, puoi essere sicuro che verrai pagato vicino a $ 80.000 perché la variazione degli stipendi è minima.
Se creassimo un boxplot per visualizzare la distribuzione degli stipendi in queste due aziende, potrebbe assomigliare a questo:
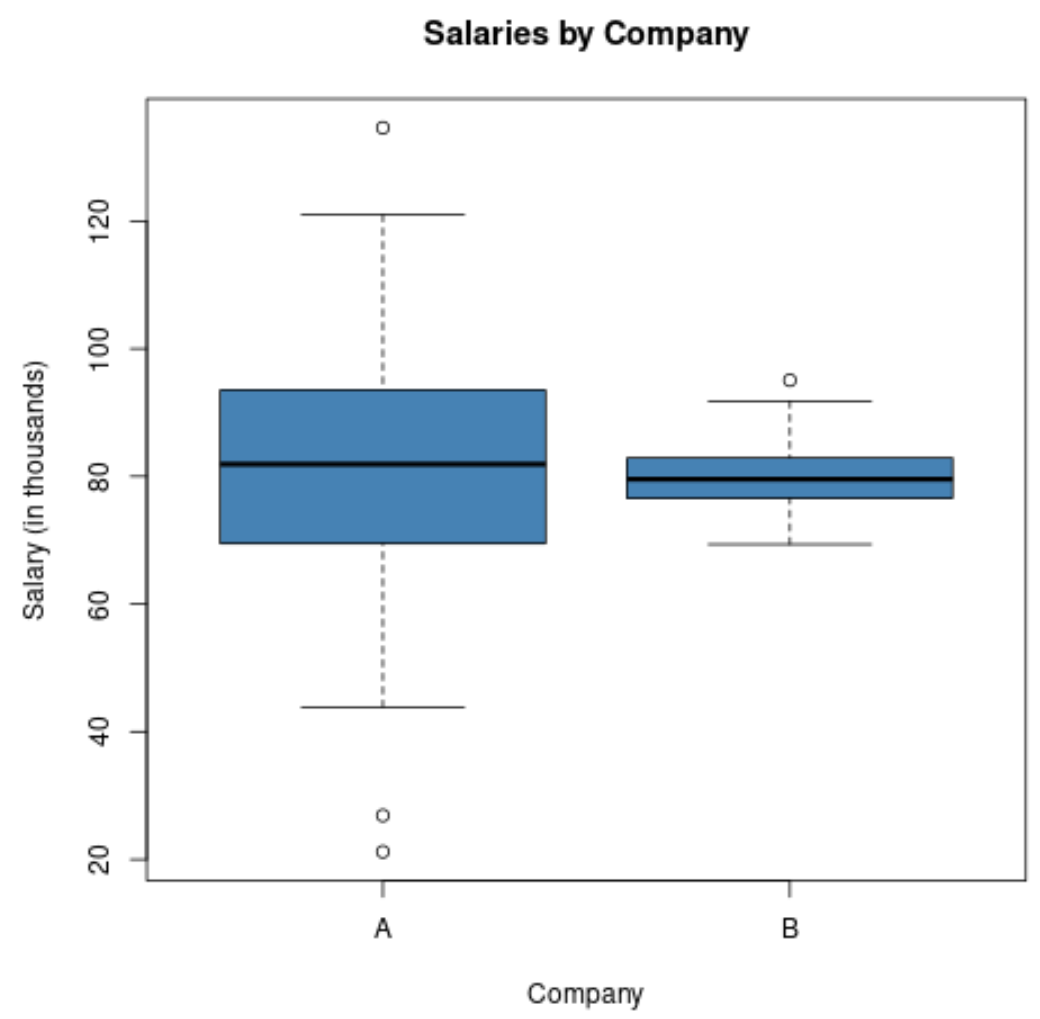
Si noti che la lunghezza del boxplot per l’azienda A è maggiore poiché la deviazione standard dei salari è molto più elevata.
Entrambe le aziende hanno lo stesso stipendio medio, ma il divario salariale è molto più elevato nell’azienda A.
Esempio 2: Distribuzione dei prezzi delle case
Supponiamo che il prezzo medio delle case nel quartiere A sia di $ 250.000 e che la deviazione standard sia di $ 50.000. Poiché la deviazione standard è piuttosto ampia, ciò significa che alcuni prezzi delle case saranno molto più alti di $ 250.000 e altri saranno molto più bassi. Se guardi una qualsiasi casa in questo quartiere, non vi è alcuna garanzia che il prezzo sia vicino alla media.
Al contrario, supponiamo che anche il prezzo medio delle case nel quartiere B sia di $ 250.000, ma la deviazione standard sia solo di $ 10.000. Poiché questa deviazione standard è piuttosto piccola, puoi essere sicuro che qualsiasi casa che guardi nel quartiere sarà probabilmente chiusa a questo prezzo.
Se creassimo un boxplot per visualizzare la distribuzione dei prezzi delle case in questi due quartieri, potrebbe assomigliare a questo:
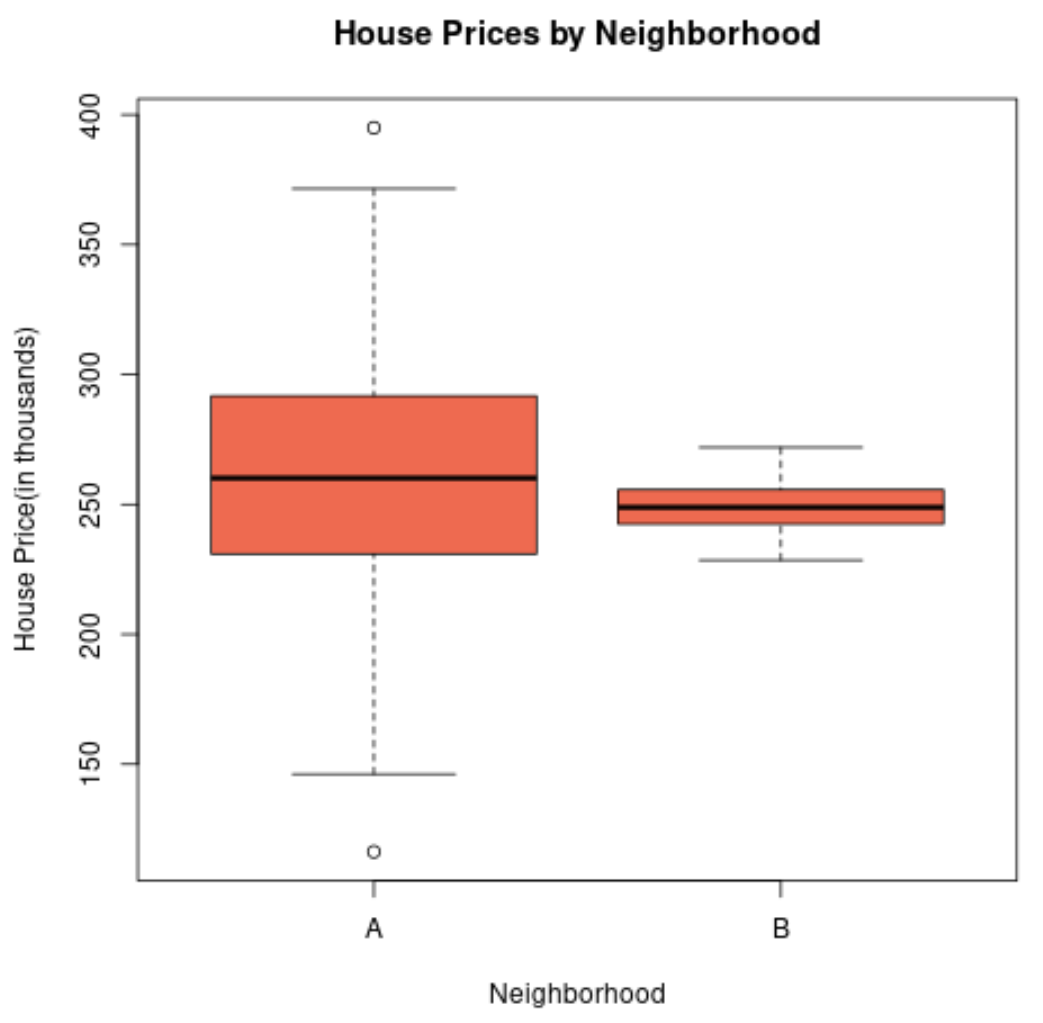
La lunghezza del boxplot del quartiere A è maggiore poiché la deviazione standard dei prezzi immobiliari è molto più elevata.
In effetti, i prezzi delle case vanno da meno di 150.000 dollari a più di 400.000 dollari per il quartiere A, mentre i prezzi vanno solo da circa 230.000 a 270.000 dollari per il quartiere B.
Conoscendo semplicemente la deviazione standard dei prezzi delle case in ciascun quartiere, possiamo sapere quanta variazione aspettarci nei prezzi in ciascun quartiere.
Risorse addizionali
Qual è considerata una buona deviazione standard?
Gamma vs. Deviazione standard: quando utilizzarli ciascuno
Coefficiente di variazione rispetto alla deviazione standard: la differenza