Probabilità vs. proporzione: qual è la differenza?
Due termini che gli studenti spesso confondono in statistica sono probabilità e proporzione .
Ecco la differenza:
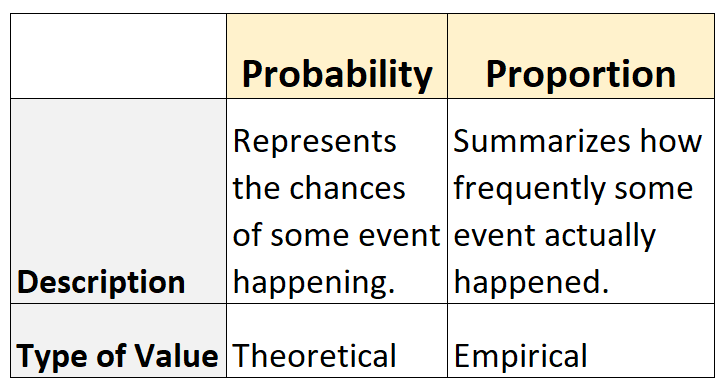
- La probabilità rappresenta la possibilità che un evento si verifichi. E’ teorico .
- La proporzione riassume la frequenza con cui un evento si è effettivamente verificato. È empirico .
Usiamo spesso probabilità per parlare delle possibilità che un evento accada in futuro.
Al contrario, spesso usiamo la proporzione per descrivere la frequenza con cui un evento è effettivamente accaduto nel passato.
Gli esempi seguenti illustrano le differenze tra probabilità e proporzioni in diversi scenari.
Esempio 1: Probabilità contro Proporzione nel lancio di una moneta
Se lanciamo una moneta equilibrata, la probabilità che esca testa è dello 0,5 o del 50% .
Tuttavia, se lanciamo una moneta 20 volte, possiamo effettivamente contare la proporzione di volte in cui è uscita testa. Ad esempio, potrebbe essere uscito testa il 60% delle volte in cui lancia.
La probabilità che la moneta esca testa è teorica, ma la proporzione di volte in cui la moneta esce testa è empirica: potremmo effettivamente contare la proporzione.
Esempio 2: Probabilità contro Proporzione nei lanci di dadi
Se lanci un dado a sei facce, la probabilità che cada sul numero “4” è 1/6 ovvero circa il 16,67% .
Tuttavia, se lanciamo il dado 10 volte, possiamo contare la proporzione di volte in cui è finito su 4. Ad esempio, forse è finito su “4” nel 20% dei tiri.
La probabilità di ottenere un “4” è teorica, ma la proporzione di volte in cui il dado è caduto su un “4” è empirica: potremmo effettivamente contare la proporzione.
Esempio 3: Probabilità vs. Proporzione nei filatori
Se giriamo una ruota della roulette divisa in quattro parti uguali – rossa, blu, verde e viola – la probabilità che finisca sul viola in ogni giro è del 25% .
Tuttavia, se giriamo la ruota della roulette 100 volte, possiamo contare la proporzione di volte in cui è finita sul viola. Ad esempio, forse è arrivato sul viola per il 15% dei giri.
La probabilità che la ruota della roulette si fermi sul viola è teorica, ma la proporzione delle volte in cui si ferma sul viola è empirica: potremmo effettivamente contare la proporzione.
Esempio 4: Probabilità contro Proporzione nei giochi di carte
In un mazzo standard da 52 carte ci sono 4 Regine. Quindi, la probabilità di scegliere una regina in un disegno è 4/52 = 7,69% .
Tuttavia, se peschiamo casualmente (e sostituiamo la carta che peschiamo) 50 volte, possiamo effettivamente contare la proporzione di volte in cui peschiamo una regina. Ad esempio, potremmo pescare una Regina nel 10% delle estrazioni.
La probabilità di scegliere una regina è teorica, ma la proporzione di volte in cui scegliamo effettivamente una regina è empirica: potremmo effettivamente contare la proporzione.
Risorse addizionali
Probabilità vs probabilità: qual è la differenza?
Legge della probabilità totale: definizione ed esempi