Come eseguire manualmente il test del chi quadrato (passo dopo passo)
Un test di bontà di adattamento chi quadrato viene utilizzato per determinare se una variabile categoriale segue o meno una distribuzione ipotetica.
Il seguente esempio passo passo mostra come eseguire manualmente un test di bontà di adattamento chi quadrato.
Test manuale della bontà di adattamento del chi quadrato
Supponiamo di credere che un certo dado sia giusto. In altre parole, crediamo che i dadi abbiano la stessa probabilità di ottenere 1, 2, 3, 4, 5 o 6 in un dato lancio.
Per testarlo, lo lanciamo 60 volte e registriamo il numero su cui si ferma ogni volta. I risultati sono i seguenti:
- 1 :8 volte
- 2 : 12 volte
- 3 : 18 volte
- 4 :9 volte
- 5 :7 volte
- 6 : 6 volte
Seguire i seguenti passaggi per eseguire un test di bontà di adattamento del chi quadrato per determinare se i dadi sono equi.
Passaggio 1: Definire le ipotesi nulla e alternativa
- H 0 (nullo): i dadi hanno la stessa probabilità di uscire su ogni numero.
- H 1 (alternativa): i dadi non hanno la stessa probabilità di uscire su ciascun numero.
Passaggio 2: calcolare le frequenze osservate e previste
Successivamente, creiamo una tabella delle frequenze osservate e attese per ciascun numero sul dado:

Nota : se pensiamo che il dado sia giusto, significa che ci aspettiamo che esca su ciascun numero un numero uguale di volte – in questo caso, 10 volte ciascuno.
Passaggio 3: calcolare la statistica del test
La statistica del test Chi-quadrato, X 2 , viene calcolata come segue:
- X2 = Σ(OE) 2 / E
La tabella seguente mostra come calcolare questa statistica del test:
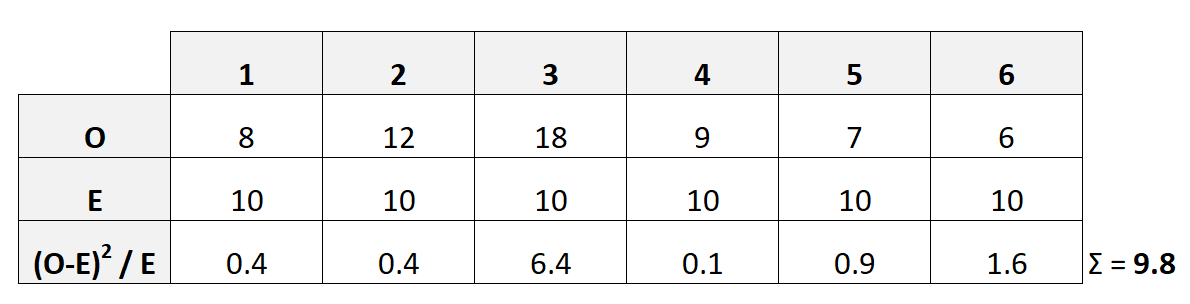
In questo caso, X 2 risulta essere 9.8 .
Passaggio 4: trovare il valore critico
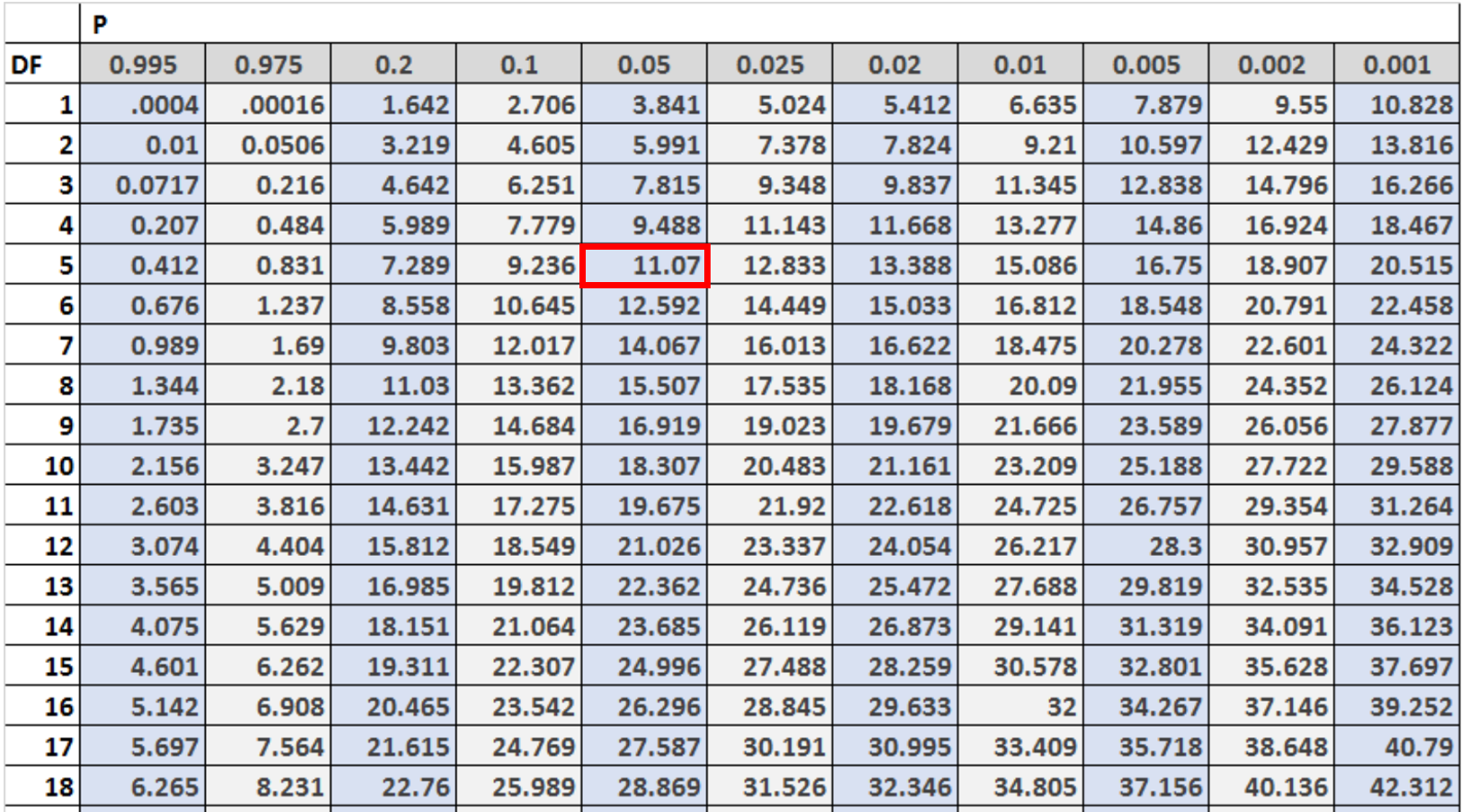
Successivamente, dobbiamo trovare il valore critico nella tabella di distribuzione del Chi-quadrato che corrisponde a α = 0,05 e df = (#categorie – 1).
In questo caso le categorie sono 6, quindi utilizzeremo df = 6 – 1 = 5 .
Possiamo vedere che il valore critico è 11.07 .
Passaggio 5: rifiutare o non rifiutare l’ipotesi nulla
Poiché la nostra statistica test è inferiore al valore critico, non riusciamo a rifiutare l’ipotesi nulla. Ciò significa che non abbiamo prove sufficienti per dire che i dadi sono ingiusti.
Risorse addizionali
Le seguenti risorse offrono ulteriori informazioni sul test della bontà di adattamento del chi quadrato:
Introduzione al test della bontà di adattamento del chi quadrato
Come eseguire un test di bontà di adattamento chi quadrato in R
Calcolatore del test di bontà di adattamento chi-quadrato