Distribuzione normale standardizzata
Questo articolo spiega cos’è la distribuzione normale standard e a cosa serve. Troverai anche le proprietà della distribuzione normale standard, la tabella con i suoi valori caratteristici e, inoltre, un esercizio risolto.
Qual è la distribuzione normale standardizzata?
La distribuzione normale standard , detta anche distribuzione normale unitaria , è il caso più semplice di distribuzione normale. Più precisamente, la distribuzione normale standard è una distribuzione normale con valori di media e deviazione standard pari rispettivamente a 0 e 1.
Pertanto, la distribuzione normale standard è definita come N(0,1), dove il primo parametro è la media della distribuzione e il secondo parametro è la sua deviazione standard (o DS).
![Rendered by QuickLaTeX.com \displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-3ca26cb58ac445099df12aeebda27e38_l3.png)
Il grafico della distribuzione normale standardizzata è quindi il seguente:
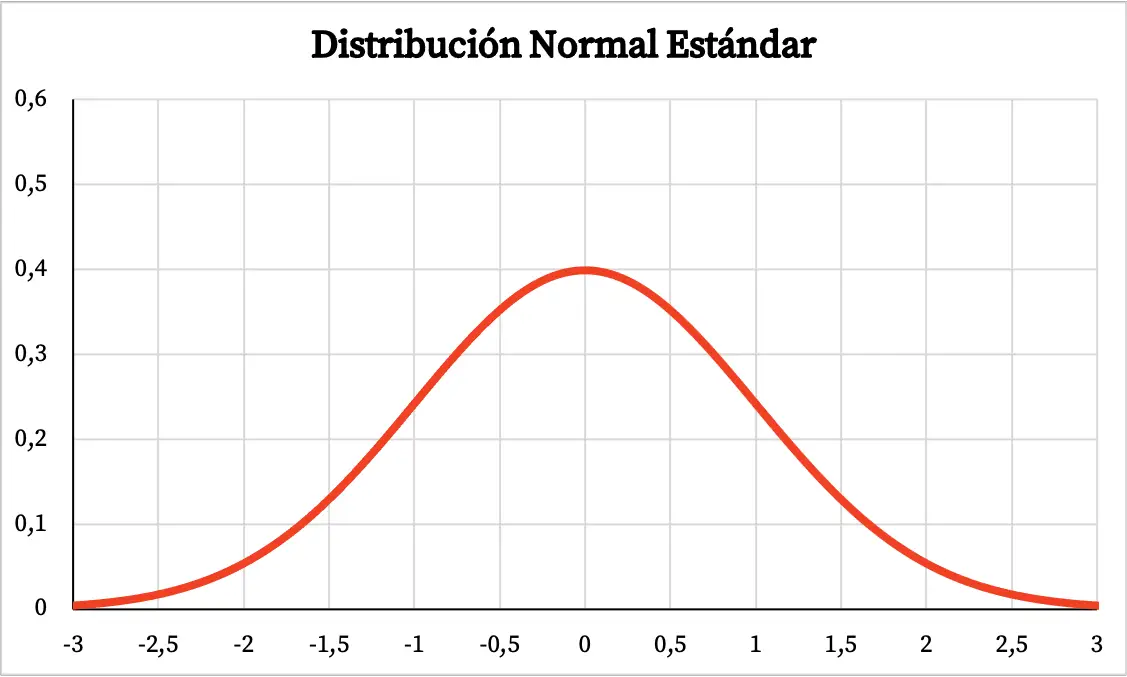
Formula per la distribuzione normale standardizzata
Per trasformare qualsiasi distribuzione normale in una distribuzione normale standard, è necessario sottrarre la media della distribuzione normale da tutti i suoi valori e poi dividerla per la deviazione standard della distribuzione normale.
La formula per la distribuzione normale standardizzata è quindi la seguente:
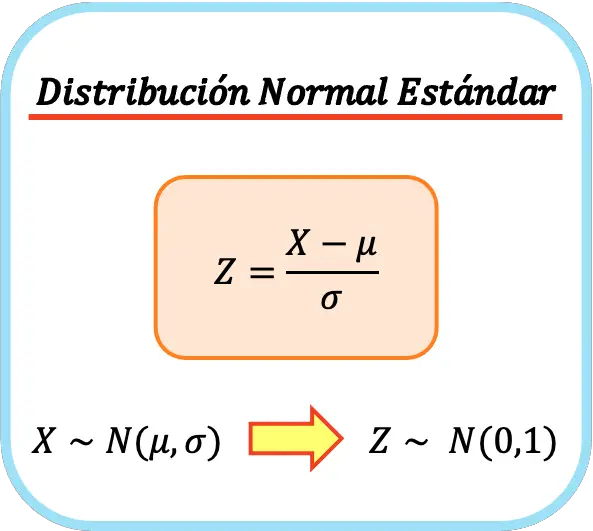
In questo modo la media aritmetica e la deviazione standard della nuova variabile saranno rispettivamente 0 e 1, quindi otterremo una distribuzione normale standardizzata. Questo processo è anche chiamato normalizzazione univariata o normalizzazione univariata .
Tabella della distribuzione normale standard
La tabella di una distribuzione normale standard è una tabella che contiene le probabilità che un valore osservato sia inferiore a un dato valore della distribuzione normale standard.
Inoltre, poiché la funzione di una distribuzione normale dipende dalla sua media e dalla deviazione standard, la tabella della distribuzione normale standard viene utilizzata anche, per estensione, per determinare le probabilità di qualsiasi distribuzione normale. Per fare ciò, la distribuzione normale viene digitata in una distribuzione normale standard e poi guardiamo nella tabella quale probabilità corrisponde ad essa.
Pertanto, i valori nella tabella della distribuzione normale standard sono i seguenti:

Esempio di distribuzione normale standard
Ora che conosciamo la definizione di distribuzione normale standard e qual è la sua formula, di seguito è riportato un esempio concreto per comprendere bene il concetto.
- Una variabile casuale continua segue una distribuzione normale con media 45 e deviazione standard 15, qual è la probabilità di ottenere un valore inferiore o uguale a 58?
![]()
Per trovare la probabilità di una distribuzione normale, dobbiamo utilizzare la sua tabella delle caratteristiche, ma per farlo dobbiamo prima eseguire il processo di digitazione per ottenere la distribuzione normale standard. Utilizziamo quindi la formula della distribuzione normale standardizzata:
![]()
Quindi sottraiamo la media dal valore di probabilità e poi dividiamo per la deviazione standard
![]()
Una volta standardizzata la variabile, andiamo alla tabella di probabilità della distribuzione normale standard (vedi sopra) per vedere a quale probabilità corrisponde il valore di 0,87:
![]()
La probabilità di ottenere un valore uguale o inferiore a 58 è quindi dell’80,78%.
Caratteristiche della distribuzione normale standardizzata
La distribuzione normale standard ha le seguenti caratteristiche:
- La distribuzione normale standard è una distribuzione simmetrica centrata su 0.
- Come una distribuzione normale, il grafico della distribuzione normale standard è a forma di campana, con la maggior parte dell’area del grafico che cade attorno alla media.
- Pertanto la media, la moda e la mediana di una distribuzione normale hanno lo stesso valore, ovvero 0.
- La distribuzione normale standard ha un massimo in z=0.
- Allo stesso modo, la distribuzione normale standard ha due punti di flesso, in z=-1 ez=+1.
- Secondo la regola pratica, sappiamo che il 68% dei valori rientra in una distribuzione normale standard compresa tra +1 e -1, il 95% dei valori tra +2 e -2 e il 99,7% dei valori tra + 3 e – 3.