Distribuzione gamma

Di Benjamin anderson Agosto 3, 2023 Probabilità 0 commenti

Questo articolo spiega cos’è la distribuzione gamma e a cosa serve. Troverai quindi la definizione della distribuzione gamma, le sue proprietà e come appare la sua rappresentazione grafica.

Qual è la distribuzione gamma?

La distribuzione gamma è una distribuzione di probabilità continua definita da due parametri caratteristici, α e λ. In altre parole, la distribuzione gamma dipende dal valore dei suoi due parametri: α è il parametro di forma e λ è il parametro di scala.

Il simbolo della distribuzione gamma è la lettera greca maiuscola Γ. Quindi, se una variabile casuale segue una distribuzione gamma, si scrive come segue:

$X\sim \Gamma(\alpha,\lambda)$

La distribuzione gamma può anche essere parametrizzata utilizzando il parametro di forma k = α e il parametro di scala inversa θ = 1/λ. In tutti i casi, i due parametri che definiscono la distribuzione gamma sono numeri reali positivi.

In genere, la distribuzione gamma viene utilizzata per modellare set di dati inclinati a destra, in modo che vi sia una maggiore concentrazione di dati sul lato sinistro del grafico. Ad esempio, la distribuzione gamma viene utilizzata per modellare l’affidabilità dei componenti elettrici.

Diagramma di distribuzione gamma

Il grafico della distribuzione gamma dipende dai valori dei suoi parametri caratteristici. Di seguito puoi vedere come varia la funzione di densità della distribuzione gamma in base al parametro di forma e al parametro di scala.

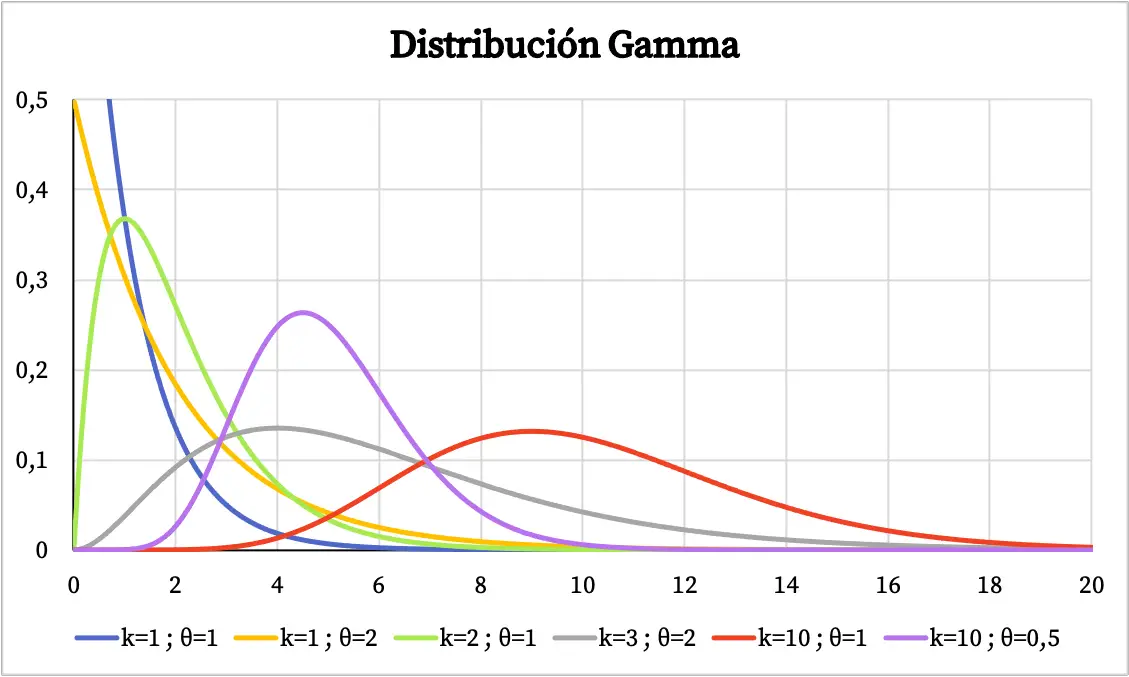
D’altra parte, puoi vedere il grafico della funzione di probabilità cumulativa della distribuzione gamma qui sotto:

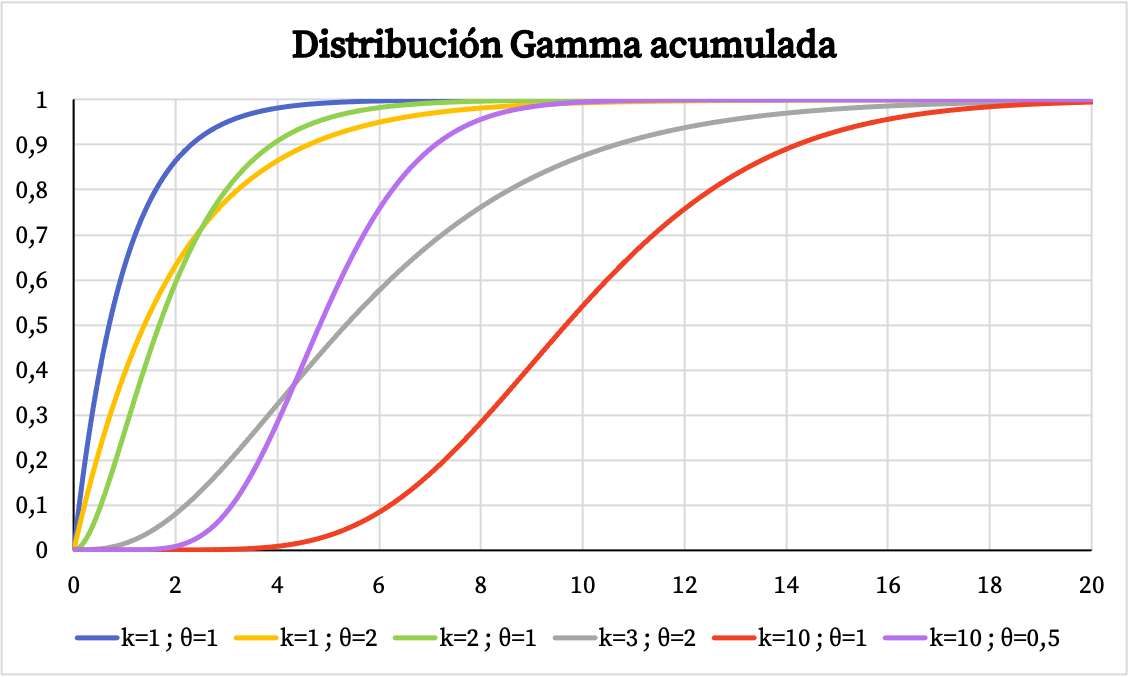
Caratteristiche della distribuzione gamma

Vedremo poi quali sono le caratteristiche della distribuzione gamma.

Il grafico della distribuzione gamma è interamente definito dai suoi due parametri caratteristici: α è il parametro di forma e λ è il parametro di scala.

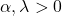
$\alpha , \lambda >0″ title=”Rendered by QuickLaTeX.com” height=”16″ width=”62″ style=”vertical-align: -4px;”></p> </p> <ul> <li> Il dominio della distribuzione gamma è composto solo da numeri positivi.</li> </ul> <p class=$ $x\in (0,+\infty)$

La media della distribuzione gamma è pari al rapporto tra il parametro di forma e il parametro di scala, ovvero α/λ.

$E[X]=\cfrac{\alpha}{\lambda}$

La varianza della distribuzione gamma è equivalente al parametro di forma diviso per il quadrato del parametro di scala.

$Var(X)=\cfrac{\alpha}{\lambda^2}$

Per valori di α inferiori a 1 la moda è 0. Ma se α è uguale o maggiore di 1, la moda della distribuzione gamma può essere calcolata con la seguente formula:

$\begin{array}{c}Mo=0 \qquad \text{para } \alpha<1\\[2ex]Mo=\cfrac{\alpha-1}{\lambda} \qquad \text{para } \alpha\geq1\end{array}$

La formula per la funzione di densità della distribuzione gamma è:

$\displaystyle f(x)=\frac{\lambda(\lambda x)^{\alpha-1}e^{-\lambda x}}{\Gamma(\alpha)}$

Dove Γ è la funzione gamma, che è definita come:

$\displaystyle \Gamma(\alpha)=\int_0^\infty t^{\alpha-1}e^{-t}dt$

La formula per la distribuzione cumulativa di una variabile casuale definita da una distribuzione gamma è la seguente:

$\displaystyle F(x)=\int_0^x\frac{\lambda(\lambda y)^{\alpha-1}e^{-\lambda y}}{\Gamma(\alpha)}\;dy$

Se il parametro di forma α è uguale a 1, allora la distribuzione gamma è equivalente a una distribuzione esponenziale con lo stesso parametro di scala λ.

$X\sim \Gamma(1,\lambda) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \text{Exp}(\lambda)$

Quando il parametro di scala λ è una media, la distribuzione gamma è un caso speciale della distribuzione chi-quadrato .

$\displaystyle X\sim \Gamma\left(\frac{n}{2},\frac{1}{2}\right) \text{con } n\in \mathbb{N}\ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \chi_n^2$

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più

Qual è la distribuzione gamma?

Diagramma di distribuzione gamma

Caratteristiche della distribuzione gamma

Informazioni sull'autore

Benjamin anderson

Aggiungi un commento