Distribuzione di weibull
Questo articolo spiega cos’è la distribuzione Weibull e a cosa serve. Inoltre, potrai vedere la rappresentazione grafica della distribuzione di Weibull e quali sono le proprietà di questo tipo di distribuzione di probabilità.
Cos’è la distribuzione di Weibull?
La distribuzione di Weibull è una distribuzione di probabilità continua definita da due parametri caratteristici: il parametro di forma α e il parametro di scala λ.
Nelle statistiche, la distribuzione di Weibull viene utilizzata principalmente per l’analisi della sopravvivenza. Allo stesso modo, la distribuzione Weibull ha molte applicazioni in diversi campi. Di seguito entreremo nei dettagli sull’utilizzo della distribuzione Weibull.
![]()
Secondo gli autori la distribuzione di Weibull può essere parametrizzata anche con tre parametri. Successivamente viene aggiunto un terzo parametro chiamato valore di soglia, che indica l’ascissa in cui inizia il grafico della distribuzione.
La distribuzione di Weibull prende il nome dallo svedese Waloddi Weibull, che la descrisse dettagliatamente nel 1951. Tuttavia, la distribuzione di Weibull fu scoperta da Maurice Fréchet nel 1927 e applicata per la prima volta da Rosin e Rammler nel 1933.
Tracciare la distribuzione di Weibull
Una volta vista la definizione della distribuzione di Weibull, vedremo come varia la sua rappresentazione grafica a seconda dei valori dei suoi parametri.
Di seguito puoi vedere diversi esempi di come varia il grafico della funzione di densità della distribuzione di Weibull a seconda del valore del parametro di forma e del parametro di scala.
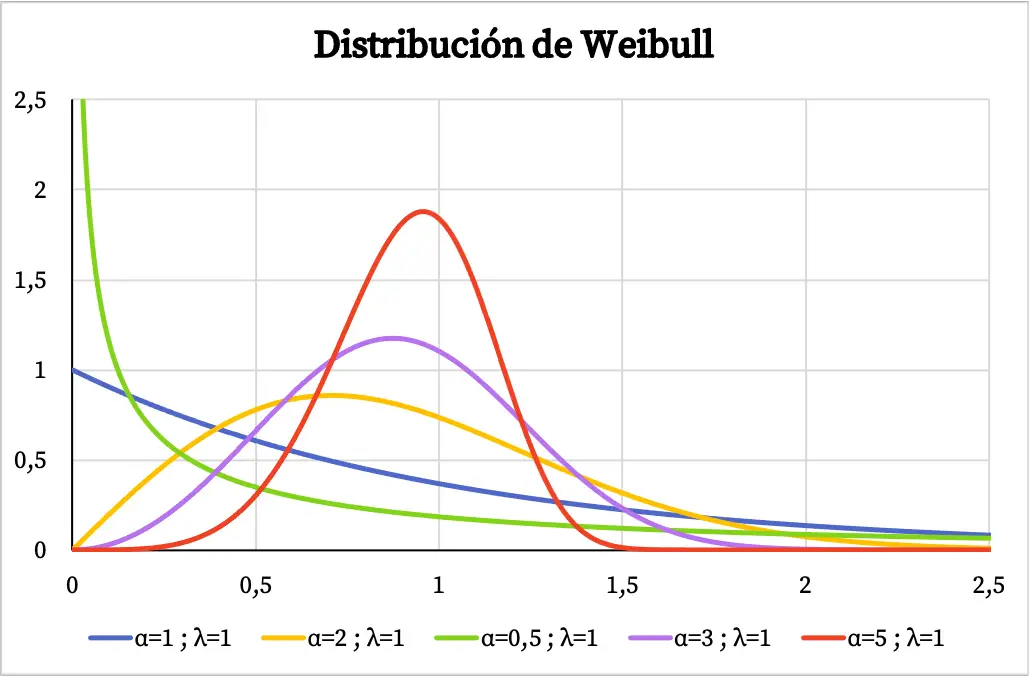
Quando la distribuzione di Weibull viene utilizzata per modellare il tasso di guasto di un sistema in funzione del tempo, il valore del parametro di forma α significa quanto segue:
- α<1: il tasso di fallimento diminuisce nel tempo.
- α=1: il tasso di guasto è costante nel tempo.
- α>1: il tasso di fallimento aumenta nel tempo.
D’altra parte, nel grafico seguente puoi vedere la funzione di probabilità cumulativa della distribuzione di Weibull tracciata in base ai suoi valori caratteristici.
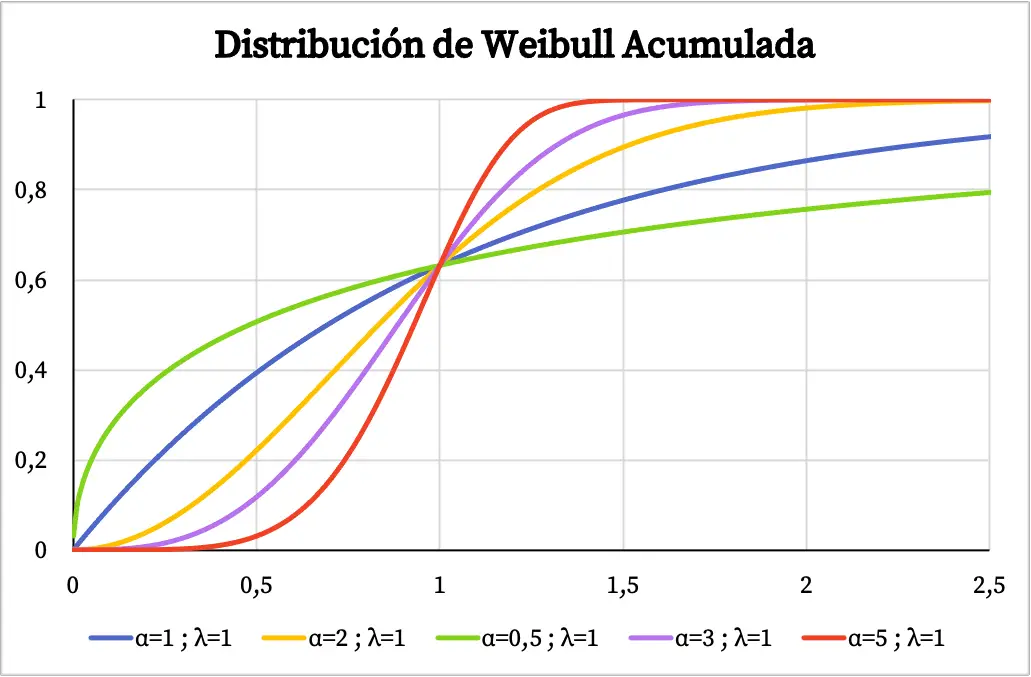
Caratteristiche della distribuzione di Weibull
La distribuzione di Weibull ha le seguenti caratteristiche:
- La distribuzione di Weibull ha due parametri caratteristici che ne definiscono il grafico: il parametro di forma α e il parametro di scala λ. Entrambi i parametri sono numeri reali positivi.
![\begin{array}{c}\alpha >0\\[2ex]\lambda >0\\[2ex]\text{Weibull}(\alpha,\lambda)\end{array}” title=”Rendered by QuickLaTeX.com” height=”92″ width=”101″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> La distribuzione Weibull accetta solo valori di ascisse positivi.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-c8794febbd607514546841a325490654_l3.png)
![]()
- La media della distribuzione di Weibull si calcola con la seguente formula:
![]()
- D’altra parte, la formula per trovare la varianza della distribuzione di Weibull è:
![]()
- La moda di una variabile casuale che segue una distribuzione di Weibull con α>1 può essere determinata dalla seguente espressione:
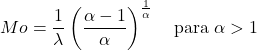
![]()
- Allo stesso modo, la formula per la funzione di probabilità cumulativa della distribuzione di Weibull è:
![]()
- Il coefficiente di asimmetria della distribuzione di Weibull si calcola applicando la seguente formula:
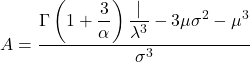
- Infine, la formula che permette di determinare il coefficiente di curtosi della distribuzione di Weibull è la seguente:
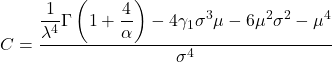
Oro
![]()
Applicazioni della distribuzione di Weibull
La distribuzione Weibull ha molte applicazioni, tra cui:
- Nella statistica applicata, la distribuzione di Weibull viene utilizzata nell’analisi della sopravvivenza.
- In ingegneria, la distribuzione di Weibull viene utilizzata per modellare le funzioni legate al tempo di produzione.
- Nei sistemi radar, per simulare la dispersione del segnale ricevuto.
- Nel settore assicurativo, per modellare l’entità dei sinistri.
- In meteorologia, ad esempio, per modellare la frequenza delle diverse velocità del vento.