Distribuzione lognormale
Questo articolo spiega cos’è la distribuzione lognormale nelle statistiche. Scoprirai quindi quali sono le proprietà della distribuzione lognormale e il grafico di questo tipo di distribuzione di probabilità.
Qual è la distribuzione lognormale?
La distribuzione lognormale , o distribuzione lognormale , è una distribuzione di probabilità che definisce una variabile casuale il cui logaritmo segue una distribuzione normale.
Pertanto, se la variabile X ha una distribuzione normale, allora la funzione esponenziale e x ha una distribuzione lognormale.
![]()
Si noti che la distribuzione lognormale può essere utilizzata solo quando i valori delle variabili sono positivi, poiché il logaritmo è una funzione che accetta solo un argomento positivo.
Tra le diverse applicazioni della distribuzione lognormale in statistica, distinguiamo l’uso di questa distribuzione per analizzare investimenti finanziari ed effettuare analisi di affidabilità.
La distribuzione lognormale è conosciuta anche come distribuzione Tinaut , a volte scritta anche come distribuzione lognormale o distribuzione lognormale .
Grafico della distribuzione lognormale
Ora che conosciamo la definizione di distribuzione lognormale, vedremo in questa sezione come varia la rappresentazione grafica della distribuzione lognormale a seconda dei valori della sua media aritmetica e della sua deviazione standard.
Il grafico della funzione di densità della distribuzione lognormale è il seguente:
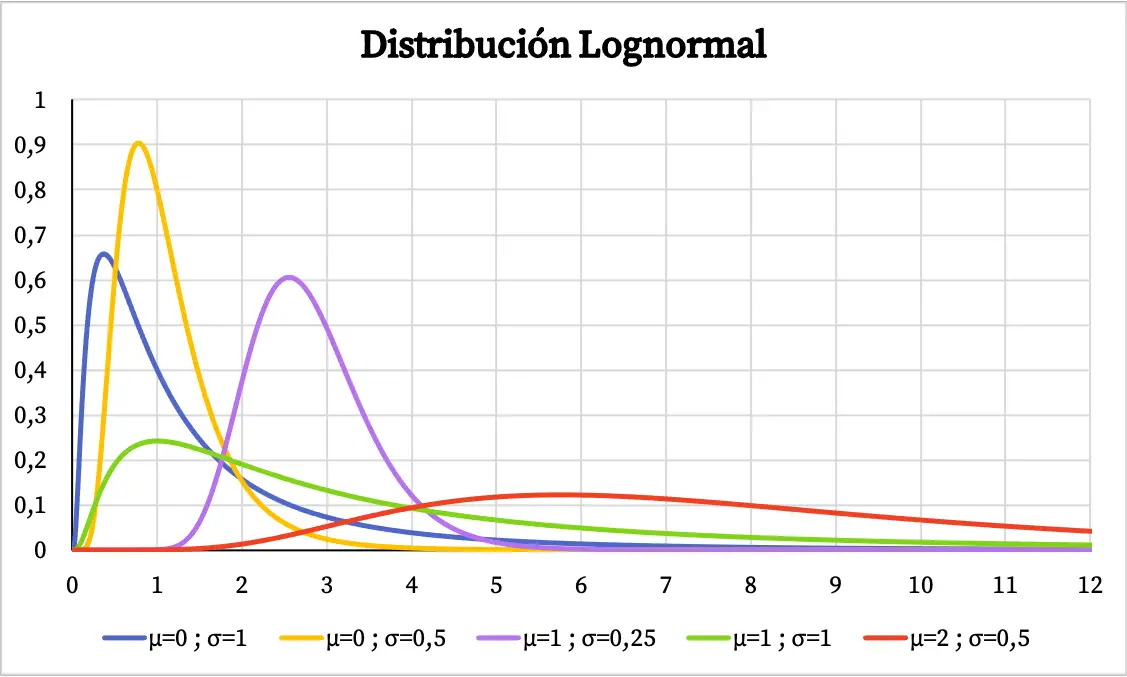
D’altra parte, il grafico della probabilità cumulativa della distribuzione lognormale è il seguente:
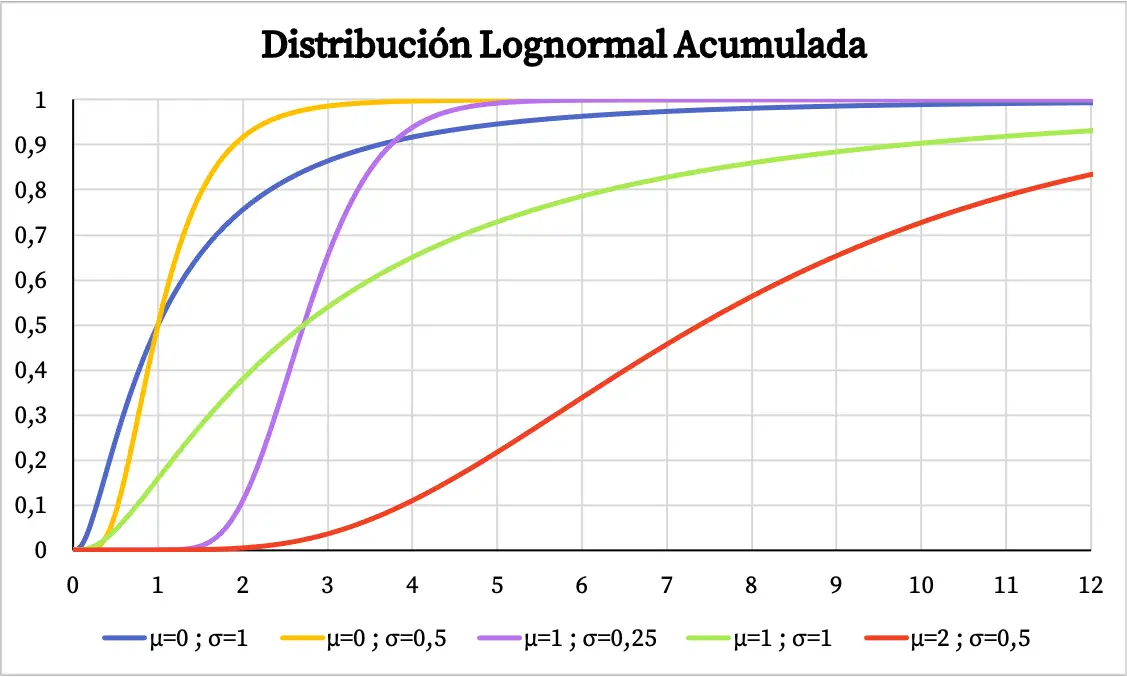
Caratteristiche della distribuzione lognormale
La distribuzione lognormale ha le seguenti caratteristiche:
- La distribuzione lognormale è definita dal valore di due parametri, la sua media aritmetica μ e la sua varianza σ 2 .
![]()
- Il dominio della distribuzione lognormale è costituito da numeri reali positivi, perché il logaritmo non accetta valori negativi o zero.
![]()
- L’aspettativa di una distribuzione lognormale è uguale al numero e elevato alla somma della media più la varianza divisa per due.
![]()
- La varianza di una distribuzione lognormale può invece essere calcolata con la seguente espressione:
![]()
- La modalità della distribuzione lognormale equivale al numero e elevato alla media della distribuzione.
![]()
- Il coefficiente di asimmetria della distribuzione lognormale può essere determinato applicando la seguente formula:
![]()
- La formula per la funzione di densità della distribuzione lognormale è:
![]()
- La formula per la funzione di probabilità cumulativa della distribuzione lognormale è:
![]()
Oro
![]()
è la funzione di probabilità cumulativa di una distribuzione normale standardizzata .
- La media aritmetica di una distribuzione lognormale è maggiore del valore della sua mediana.
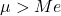
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più