Distribuzione di pareto
Questo articolo spiega cos’è la distribuzione di Pareto nelle statistiche e a cosa serve. Potrai anche vedere il grafico della distribuzione di Pareto e le proprietà di questo tipo di distribuzione di probabilità.
Cos’è la distribuzione di Pareto?
La distribuzione di Pareto è una distribuzione di probabilità continua utilizzata in statistica per modellare il principio di Pareto. Pertanto, la distribuzione di Pareto è una distribuzione di probabilità che ha pochi valori la cui probabilità di accadimento è molto più alta rispetto al resto dei valori.
Ricordiamo che la legge di Pareto, detta anche regola 80-20, è un principio statistico secondo il quale la maggior parte della causa di un fenomeno è dovuta ad una piccola parte della popolazione.
La distribuzione di Pareto ha due parametri caratteristici: il parametro di scala x m e il parametro di forma α.
![]()
In origine, la distribuzione di Pareto veniva utilizzata per descrivere la distribuzione della ricchezza all’interno della popolazione, poiché la maggior parte di essa era dovuta ad una piccola percentuale della popolazione. Ma attualmente la distribuzione di Pareto ha molteplici applicazioni, ad esempio nel controllo della qualità, in economia, nella scienza, in campo sociale, ecc.
La distribuzione di Pareto prende il nome dall’economista Vilfredo Pareto, che la formulò. Tuttavia, è meglio conosciuto per il grafico di Pareto.
Tabella di distribuzione di Pareto
Ora che conosciamo la definizione di distribuzione di Pareto, diamo un’occhiata ad alcuni esempi di distribuzioni di Pareto rappresentate graficamente.
Quindi, di seguito puoi vedere come appare il grafico della funzione di densità della distribuzione di Pareto in base ai suoi valori caratteristici:
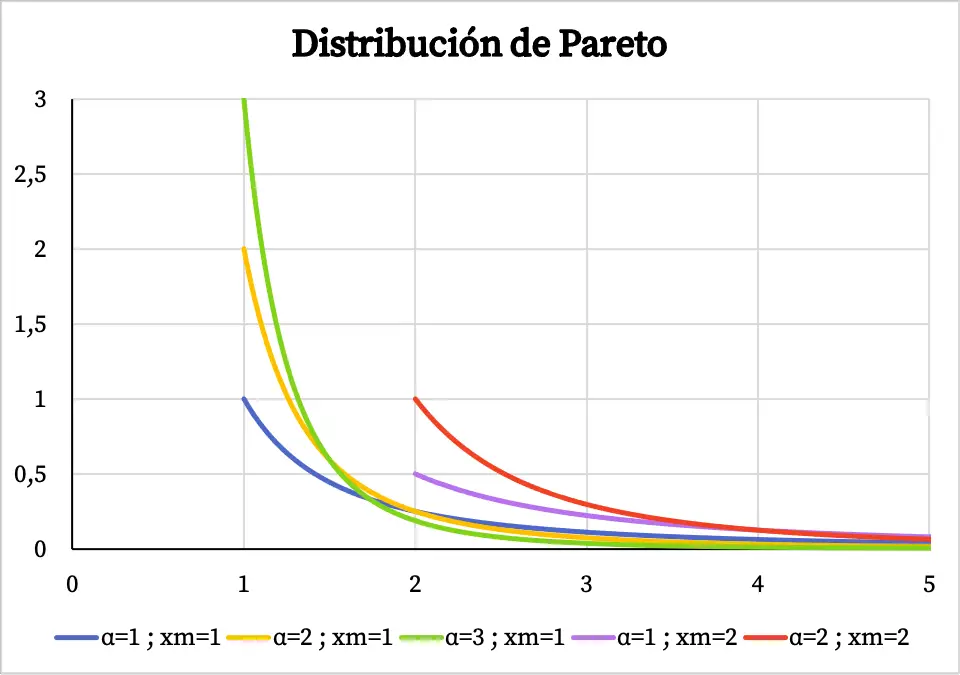
Si noti che il dominio della distribuzione di Pareto va dal valore x m a +∞, motivo per cui la funzione di densità non esiste prima del valore di x m .
D’altra parte, il grafico della funzione di probabilità cumulativa della distribuzione di Pareto è il seguente:
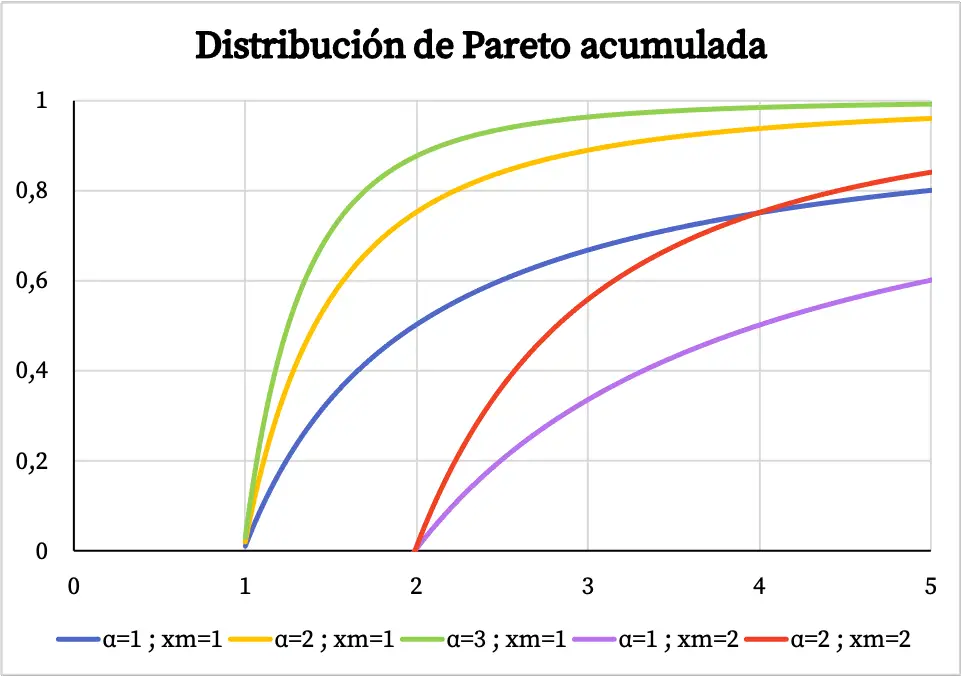
Caratteristiche della distribuzione di Pareto
Di seguito sono riportate le caratteristiche più importanti della distribuzione di Pareto relative alla teoria e alla statistica della probabilità.
- La distribuzione di Pareto ha due parametri caratteristici che definiscono la sua curva: il parametro di scala x m e il parametro di forma α.
![]()
- Il dominio della distribuzione di Pareto è costituito da tutti i numeri reali dal parametro di scala a più infinito.
![]()
- Se α è maggiore di 1, la media della distribuzione di Pareto è uguale al prodotto di α per x m e α meno 1.
![E[X]=\cfrac{\alpha\cdot x_m}{\alpha-1}\quad\text{para } \alpha>1″ title=”Rendered by QuickLaTeX.com” height=”34″ width=”214″ style=”vertical-align: -12px;”></p>
</p>
<ul>
<li> La varianza della distribuzione di Pareto dipende dai due parametri caratteristici della distribuzione e si calcola con la seguente formula:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-6d26513868f9ed6fa45ab0fde0030884_l3.png)
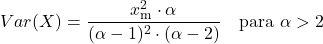
![]()
- La modalità della distribuzione di Pareto è equivalente al parametro di scala x m della distribuzione.
![]()
- La formula per la funzione di densità della distribuzione di Pareto è:
![]()
- Allo stesso modo, la formula per la funzione di probabilità cumulativa della distribuzione di Pareto è:
![]()
- Il coefficiente di asimmetria della distribuzione di Pareto dipende solo dal parametro di forma α e la sua espressione è:
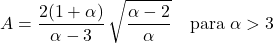
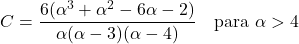
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più