Intervallo di confidenza per la proporzione

Di Benjamin anderson Agosto 3, 2023 Statistiche 0 commenti

Questo articolo spiega cos’è l’intervallo di confidenza per la proporzione e a cosa serve nelle statistiche. Allo stesso modo, scoprirai come calcolare l’intervallo di confidenza della proporzione e un esercizio risolto per comprendere meglio il concetto.

Qual è l’intervallo di confidenza della proporzione?

L’ intervallo di confidenza per la proporzione è un intervallo che fornisce un intervallo di valori ammissibili per la proporzione di una popolazione. Cioè, l’intervallo di confidenza per la proporzione indica un valore massimo e un valore minimo tra i quali si trova la proporzione della popolazione con un margine di errore.

Ad esempio, se l’intervallo di confidenza per la proporzione di una popolazione con un livello di confidenza del 95% è (0,73, 0,81), ciò significa che la proporzione di una popolazione è compresa tra il 73% e l’81% con una probabilità del 95%.

Pertanto, l’intervallo di confidenza della proporzione viene utilizzato per stimare il valore della proporzione di una popolazione che soddisfa determinate caratteristiche.

Come vedremo nella sezione successiva, l’intervallo di confidenza per la proporzione dipende dalla proporzione del campione e dal numero di osservazioni nel campione.

Formula dell’intervallo di confidenza per la proporzione

L’intervallo di confidenza per la proporzione viene calcolato aggiungendo e sottraendo dalla proporzione campionaria il valore di Z _α/2 moltiplicato per la radice quadrata della proporzione campionaria (p) moltiplicata per 1-p e divisa per la dimensione del campione (n). Pertanto, la formula per calcolare l’intervallo di confidenza per la proporzione è:

$\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)$

Oro:

$p$

è la proporzione campionaria.
$n$

è la dimensione del campione.
$Z_{\alpha/2}$

è il quantile della distribuzione normale standard corrispondente a una probabilità di α/2. Per campioni di grandi dimensioni e un livello di confidenza del 95% è solitamente vicino a 1,96 mentre per un livello di confidenza del 99% è solitamente vicino a 2,576.

Esempio di calcolo di un intervallo di confidenza per la proporzione

Affinché tu possa vedere come viene calcolato un intervallo di confidenza per la proporzione, ti lasciamo di seguito un esempio concreto passo dopo passo.

Una compagnia assicurativa vuole condurre ricerche di mercato e determinare quante persone in un paese hanno un’assicurazione sulla vita. Per fare questo si analizza un campione casuale di 700 persone e si arriva alla conclusione che il 40% del campione ha un’assicurazione sulla vita. Qual è l’intervallo di confidenza al livello di confidenza del 95% per la percentuale della popolazione del paese?

Per determinare l’intervallo di confidenza della proporzione della popolazione, dobbiamo utilizzare la formula che abbiamo visto sopra:

$\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)$

In questo caso, vogliamo che il livello di confidenza dell’intervallo di confidenza sia del 95%, quindi il valore di Z _α/2 che dobbiamo prendere è 1,96.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

La formulazione del problema ci dice già che la dimensione del campione è n=700 e la proporzione osservata nel campione è p=0,40, quindi sostituiamo i dati nella formula dell’intervallo di confidenza per la proporzione e calcoliamo i limiti dell’intervallo:

$\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)$

$\displaystyle \left(0,40-1,96\cdot \sqrt{\frac{0,40\cdot (1-0,40)}{700}}\ , \ 0,40+1,96\cdot \sqrt{\frac{0,40\cdot (1-0,40)}{700}\right)$

$\displaystyle \left(0,36 \ , \ 0,44\right)$

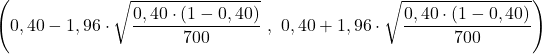
In conclusione, la percentuale della popolazione studiata è compresa tra il 36% e il 44% con un livello di confidenza del 95%.

➤ Vedi: Intervallo di confidenza per la media
➤ Vedi: Intervallo di confidenza per la varianza

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più

Qual è l’intervallo di confidenza della proporzione?

Formula dell’intervallo di confidenza per la proporzione

Esempio di calcolo di un intervallo di confidenza per la proporzione

Informazioni sull'autore

Benjamin anderson

Aggiungi un commento