Verifica di ipotesi per la media

Di Benjamin anderson Agosto 3, 2023 Statistiche 0 commenti

Questo articolo spiega cos’è il test di ipotesi per la media nelle statistiche. Troverai quindi la formula del test di ipotesi per la media e, inoltre, un esercizio risolto passo dopo passo.

Cos’è il test di ipotesi per la media?

Il test di ipotesi per la media è un metodo statistico utilizzato per rifiutare o rifiutare l’ipotesi nulla di una media della popolazione.

Più specificamente, il test dell’ipotesi per la media implica il calcolo della statistica del test e il confronto con il valore critico per rifiutare o meno l’ipotesi nulla.

Va notato che i test di ipotesi hanno nomi diversi; in statistica sono anche chiamati contrasti di ipotesi, test di ipotesi o test di significatività.

Formula di verifica delle ipotesi per la media

Successivamente vedremo come viene calcolata la statistica del test di ipotesi per la media. Tuttavia la formula varia leggermente a seconda che la varianza sia nota o meno, quindi vedremo prima come si fa quando la varianza è nota e poi quando la varianza è sconosciuta.

Con deviazione nota

La formula dell’ipotesi di test per la media con varianza nota è:

$\displaystyle Z=\frac{\overline{x}-\mu}{\displaystyle \frac{\sigma}{\sqrt{n}}}$

Oro:

$Z$

è la statistica del test di ipotesi per la media.
$\overline{x}$

è la media del campione.
$\mu$

è il valore medio proposto.
$\sigma$

è la deviazione standard della popolazione.
$n$

è la dimensione del campione.

Una volta calcolata la statistica del test di ipotesi per la media, il risultato deve essere interpretato per rifiutare o rifiutare l’ipotesi nulla:

Se il test di ipotesi per la media è bilaterale, l’ipotesi nulla viene rifiutata se il valore assoluto della statistica è maggiore del valore critico Z _α/2 .
Se il test di ipotesi per la media corrisponde alla coda destra, l’ipotesi nulla viene rifiutata se la statistica è maggiore del valore critico Z _α .
Se il test di ipotesi per la media corrisponde alla coda sinistra, l’ipotesi nulla viene rifiutata se la statistica è inferiore al valore critico -Z _α .

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}$

In questo caso i valori critici si ottengono dalla tabella della distribuzione normale standardizzata .

Con varianza sconosciuta

La formula dell’ipotesi di test per la media con varianza sconosciuta è:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

Oro:

$t$

è la statistica di verifica dell’ipotesi per la media, che è definita dalla distribuzione t di Student .
$\overline{x}$

è la media del campione.
$\mu$

è il valore medio proposto.
$s$

è la deviazione standard del campione.
$n$

è la dimensione del campione.

Come prima, il risultato calcolato della statistica test deve essere interpretato con il valore critico per rifiutare o meno l’ipotesi nulla:

Se il test di ipotesi per la media è bilaterale, l’ipotesi nulla viene rifiutata se il valore assoluto della statistica è maggiore del valore critico t _α/2|n-1 .
Se il test di ipotesi per la media corrisponde alla coda destra, l’ipotesi nulla viene rifiutata se la statistica è maggiore del valore critico t _α|n-1 .
Se il test di ipotesi per la media corrisponde alla coda sinistra, l’ipotesi nulla viene rifiutata se la statistica è inferiore al valore critico -t _α|n-1 .

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

Quando la varianza è sconosciuta, i valori critici del test si ottengono dalla tabella di distribuzione di Student.

Esempio nel mondo reale di verifica di ipotesi per la media

Per comprendere appieno il concetto di verifica di ipotesi per la media della popolazione, di seguito è possibile vedere un esempio reale di questo tipo di verifica di ipotesi.

Una società tecnologica afferma che la batteria del laptop che vende dura 6 ore. Verifichiamo se questa ipotesi è falsa eseguendo un test di ipotesi con un livello di significatività α = 0,05. Per fare ciò si decide di acquistare 20 unità e di osservare la durata della batteria di ciascun computer (i valori sono espressi in ore):

5,2 5,9 7,1 4,2 6,5
8,5 4,6 6,8 6,9 5,8
5.1 6.5 7.0 5.3 6.2
5,7 6,6 7,5 5,1 6,1

In questo caso, le ipotesi nulla e alternativa del test di ipotesi sulla media sono le seguenti:

$\begin{cases}H_0: \mu=6\\[2ex] H_1:\mu\neq 6 \end{cases}$

Per determinare la statistica del test, dobbiamo prima calcolare la media campionaria e la deviazione standard campionaria:

$\overline{x}=6,13 \qquad s=1,05$

Poiché non conosciamo la varianza della popolazione, per ottenere la statistica del test dobbiamo applicare la formula di verifica delle ipotesi per la media con varianza sconosciuta:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

$\displaystyle t=\frac{6,13-6}{\displaystyle \frac{1,05}{\sqrt{20}}}$

$\displaystyle t=0,68$

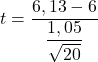
Ora dobbiamo trovare il valore critico del test di ipotesi, quindi cerchiamo il valore corrispondente nella tabella della distribuzione t di Student . I gradi di libertà del t di Student sono uno in meno rispetto alla dimensione del campione (20-1=19) e, d’altro canto, la probabilità corrispondente è la metà del livello di significatività (0,05/2= 0,025) poiché si tratta di un’equazione a due code. controllo di un’ipotesi.

$\alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 19}=2,093\end{array}$

In conclusione, poiché si tratta di un test di ipotesi a due code e il valore assoluto della statistica test è inferiore al valore critico, non si rifiuta l’ipotesi nulla, ma si rifiuta l’ipotesi alternativa.

$0,68<2,093 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_1$

Verifica di ipotesi per la differenza nelle medie

Il test dell’ipotesi della differenza delle medie viene utilizzato per rifiutare o accettare l’ipotesi nulla secondo cui le medie di due popolazioni sono le stesse.

Pertanto l’ipotesi nulla di un test di ipotesi per la differenza di due medie è sempre la seguente:

$H_0: \mu_1=\mu_2$

Mentre l’ipotesi alternativa può essere una delle seguenti tre:

$\begin{array}{l}H_1:\mu_1\neq \mu_2\\[2ex]H_1:\mu_1>\mu_2\\[2ex]H_1:\mu_1<\mu_2\end{array}$

Quindi, la formula per calcolare la statistica del test di ipotesi per la differenza nelle medie quando la varianza è nota è:

$\displaystyle Z=\frac{\displaystyle \overline{x_1}-\overline{x_2}}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

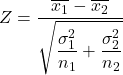
Oro:

$Z$

è l’ipotesi che verifica la statistica per la differenza di due medie con varianza nota, che segue una distribuzione normale standard.
$\overline{x_1}$

è la media del campione 1.
$\overline{x_2}$

è la media del campione 2.
$\sigma_1^2$

è la varianza della popolazione 1.
$\sigma_2^2$

è la varianza della popolazione 2.
$n_1$

è la dimensione del campione 1.
$n_2$

è la dimensione del campione 2.

D’altra parte, la formula per calcolare la statistica del test di ipotesi per la differenza tra le medie quando la varianza è sconosciuta è la seguente:

$\displaystyle t=\frac{\displaystyle \overline{x_1}-\overline{x_2}}{\displaystyle\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

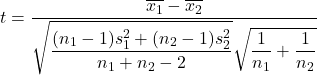
Oro:

$t$

è la statistica di verifica dell’ipotesi per la differenza di due medie con varianza sconosciuta, che segue la distribuzione t di Student.
$\overline{x_1}$

è la media del campione 1.
$\overline{x_2}$

è la media del campione 2.
$s_1^2$

è la varianza del campione 1.
$s_2^2$

è la varianza del campione 2.
$n_1$

è la dimensione del campione 1.
$n_2$

è la dimensione del campione 2.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più

Cos’è il test di ipotesi per la media?

Formula di verifica delle ipotesi per la media

Con deviazione nota

Con varianza sconosciuta

Esempio nel mondo reale di verifica di ipotesi per la media

Verifica di ipotesi per la differenza nelle medie

Informazioni sull'autore

Benjamin anderson

Aggiungi un commento