Verifica di ipotesi per la proporzione

Di Benjamin anderson Agosto 3, 2023 Statistiche 0 commenti

Questo articolo spiega quale sia il test delle ipotesi sulle proporzioni nelle statistiche. Troverai quindi la formula del test di ipotesi sulla proporzione e, inoltre, un esercizio passo passo per comprendere appieno come si effettua.

Cos’è il test di ipotesi per la proporzione?

Il test dell’ipotesi proporzionale è un metodo statistico utilizzato per determinare se rifiutare o meno l’ipotesi nulla di una proporzione della popolazione.

Quindi, a seconda del valore della statistica del test di ipotesi per la proporzione e il livello di significatività, l’ipotesi nulla viene rifiutata o accettata.

Si noti che il test di ipotesi può anche essere chiamato test di ipotesi di contrasto, test di ipotesi o test di significatività.

Formula di verifica delle ipotesi per la proporzione

La statistica del test di ipotesi per la proporzione è uguale alla differenza nella proporzione campionaria meno il valore proposto della proporzione diviso per la deviazione standard della proporzione.

La formula dell’ipotesi di test per la proporzione è quindi:

$\displaystyle Z=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}$

Oro:

$Z$

è la statistica del test di ipotesi per la proporzione.
$\widehat{p}$

è la proporzione campionaria.
$p$

è il valore della proporzione proposta.
$n$

è la dimensione del campione.
$\displaystyle\sqrt{\frac{p(1-p)}{n}}$

è la deviazione standard della proporzione.

Tieni presente che non è sufficiente calcolare la statistica del test di ipotesi per la proporzione, ma il risultato deve poi essere interpretato:

Se il test di ipotesi per la proporzione è bilaterale, l’ipotesi nulla viene rifiutata se il valore assoluto della statistica è maggiore del valore critico Z _α/2 .
Se il test di ipotesi per la proporzione corrisponde alla coda destra, l’ipotesi nulla viene rifiutata se la statistica è maggiore del valore critico Z _α .
Se il test di ipotesi per la proporzione corrisponde alla coda sinistra, l’ipotesi nulla viene rifiutata se la statistica è inferiore al valore critico -Z _α .

$\begin{array}{l}H_1: p\neq p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: p> p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: p< p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}$

Ricorda che i valori critici possono essere facilmente ottenuti dalla tabella di distribuzione normale.

➤ Vedi: tabella della distribuzione normale

Esempio di verifica di ipotesi per la proporzione

Una volta che vediamo la definizione di test di ipotesi per proporzione e qual è la sua formula, risolveremo un esempio per comprendere meglio il concetto.

Secondo il produttore, un farmaco contro una malattia specifica ha un’efficacia del 70%. In laboratorio testiamo l’efficacia di questo farmaco poiché i ricercatori ritengono che la proporzione sia diversa. Per questo il farmaco viene testato su un campione di 1.000 pazienti e 641 persone guariscono. Eseguire un test di ipotesi sulla proporzione della popolazione con un livello di significatività del 5% per rifiutare o meno l’ipotesi dei ricercatori.

In questo caso, l’ipotesi nulla e l’ipotesi alternativa del test di ipotesi per la proporzione della popolazione sono:

$\begin{cases}H_0: p=0,70\\[2ex] H_1:p\neq 0,70 \end{cases}$

La percentuale di persone nel campione che sono guarite dal farmaco è:

$\widehat{p}=\cfrac{641}{1000}=0,641$

Calcoliamo la statistica del test di ipotesi per la proporzione applicando la formula vista sopra:

$\begin{aligned} \displaystyle Z&=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}\\[2ex]Z&=\frac{0,641-0,70}{\displaystyle\sqrt{\frac{0,70\cdot (1-0,70)}{1000}}} \\[2ex] Z&=-4,07\end{aligned}}$

D’altra parte, poiché il livello di significatività è 0,05 e questo è un test di ipotesi a due code, il valore critico del test è 1,96.

$Z_{0,025}=1,96$

➤ Vedi: Livello di significatività 0,05

In conclusione, il valore assoluto della statistica test è maggiore del valore critico, quindi rifiutiamo l’ipotesi nulla e accettiamo l’ipotesi alternativa.

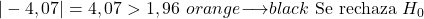$|-4,07|=4,07>1,96 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_0″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”424″ style=”vertical-align: -5px;”></p> </p> <div style=$ ➤ Vedi: Verifica di ipotesi per la media

Verifica di ipotesi per due proporzioni campione

Il test di ipotesi sulle proporzioni di due campioni viene utilizzato per rifiutare o accettare l’ipotesi nulla che le proporzioni di due diverse popolazioni siano uguali.

Pertanto, l’ipotesi nulla di un test di ipotesi per proporzioni a due campioni è sempre:

$H_0: p_1=p_2$

Mentre l’ipotesi alternativa può essere una delle tre opzioni:

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}H_1:p_1\neq p_2\\[2ex]H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio of the two samples is calculated as follows:[latex]p=\cfrac {x_1+x_2}{n_1+n_2}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ...H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio
Please use \mathaccent for accents in math mode.
leading text: ...\[2ex]H_1:p_1 The combined ratio of the two
Please use \mathaccent for accents in math mode.
leading text: ...combined of the two samples is calculated
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.

E la formula per calcolare la statistica del test di ipotesi per due proporzioni campionarie è:

$\displaystyle Z=\frac{\displaystyle \frac{x_1}{n_1}-\frac{x_2}{n_2}}{\displaystyle \sqrt{p(1-p)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}$

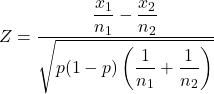
Oro:

$Z$

è la statistica del test di ipotesi per proporzioni a due campioni.
$x_1$

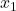
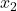
è il numero di risultati nel campione 1.
$x_2$

è il numero di risultati nel campione 2.
$n_1$

è la dimensione del campione 1.
$n_2$

è la dimensione del campione 2.
$p$

è la proporzione combinata dei due campioni.

Verifica di ipotesi per k proporzioni campionarie

In un test di ipotesi sulle proporzioni di k campioni, l’obiettivo è determinare se tutte le proporzioni delle diverse popolazioni sono uguali o, al contrario, se esistono proporzioni diverse. Pertanto l’ipotesi nulla e l’ipotesi alternativa in questo caso sono:

$\begin{cases}H_0: \text{Todas las proporciones son iguales}\\[2ex] H_1: \text{No todas las proporciones son iguales} \end{cases}$

In questo caso, la proporzione combinata di tutti i campioni viene calcolata come segue:

$p=\cfrac{\displaystyle\sum_{i=1}^k x_i}{\displaystyle\sum_{i=1}^k n_i}=\cfrac{x_1+x_2+\dots+x_k}{n_1+n_2+\dots+n_k}$

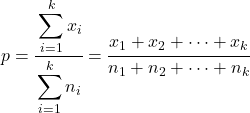
La formula per trovare la statistica del test di ipotesi per k proporzioni campionarie è:

$\displaystyle \chi^2 =\sum_{i=1}^k \frac{(x_i-e_i)^2}{e_i}$

$\displaystyle\chi^2 = \frac{(x_1-e_1)^2}{e_1} +\frac{(x_2-e_2)^2}{e_2} +\dots+\frac{(x_k-e_k)^2}{e_k}$

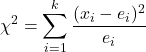
Oro:

$\chi^2$

è la statistica del test di ipotesi per k proporzioni campionarie. In questo caso, la statistica segue una distribuzione chi-quadrato.
$x_i$

è il numero di risultati nel campione i.
$n_i$

è la dimensione del campione i.
$p$

è la proporzione combinata di tutti i campioni.
$e_i$

è il numero di risultati attesi dal campione i. Si calcola moltiplicando la proporzione combinata

$p$

per dimensione del campione

$n_i$

.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più

Cos’è il test di ipotesi per la proporzione?

Formula di verifica delle ipotesi per la proporzione

Esempio di verifica di ipotesi per la proporzione

Verifica di ipotesi per due proporzioni campione

Verifica di ipotesi per k proporzioni campionarie

Informazioni sull'autore

Benjamin anderson

Aggiungi un commento