Media campionaria
In questo articolo scoprirai qual è la media campionaria nelle statistiche. Allo stesso modo, troverai come calcolare la media di un campione, un esercizio risolto e, inoltre, un calcolatore online per calcolare la media di qualsiasi campione.
Qual è la media del campione?
In statistica, la media campionaria è la media dei valori di un campione. Per calcolare la media campionaria è necessario sommare tutti i valori del campione e poi dividerli per il numero totale di dati presenti nel campione.
Il simbolo per la media del campione è
![]()
.
In uno studio statistico, generalmente non tutti i valori di una popolazione sono noti, motivo per cui viene selezionato un campione della popolazione per analizzarlo ed estrapolare le conclusioni ottenute all’intera popolazione. Pertanto, la media campionaria viene utilizzata per stimare la media della popolazione.
Esempio di formula media
La media campionaria è uguale alla somma di tutti i valori del campione divisa per la dimensione del campione. Cioè, per calcolare la media campionaria, tutti i valori del campione vengono sommati e poi divisi per il numero totale di dati nel campione.
Pertanto la formula per calcolare la media campionaria è:

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare la media campionaria di qualsiasi set di dati.
Tieni presente che la media del campione viene calcolata utilizzando i dati di un campione, quindi il valore della media della popolazione potrebbe differire dal valore calcolato.
Esempio di calcolo della media del campione
Ora che conosciamo la definizione di media campionaria e qual è la sua formula, vediamo come ottenere la media campionaria da un set di dati risolvendo un semplice esempio.
- Jose vuole trasferirsi in centro città, ma non ha molto tempo e non può analizzare i prezzi di tutti gli appartamenti in affitto. Quindi decidi di guardare solo il prezzo di affitto di cinque appartamenti (mostrato sotto) per scoprire quanto ti costerà vivere in centro. Qual è il prezzo medio del campione?
€ 600 € 430 € 820 € 575 € 950
Per trovare la media campionaria, dobbiamo sommare tutti i valori campionari e poi dividerli per il numero totale di osservazioni, che è 5. Quindi, applichiamo la formula della media campionaria:
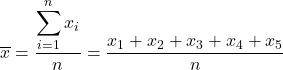
Successivamente, sostituiamo i dati nella formula e calcoliamo la media campionaria:
![]()
In sintesi, il prezzo medio del campione di appartamenti selezionato per il campione è di 675 euro.
Esempio di calcolo della media
Inserisci i dati di qualsiasi campione statistico nel seguente calcolatore per calcolarne la media campionaria. I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.
Media campionaria e media della popolazione
La media della popolazione è la media della popolazione statistica . La media della popolazione è quindi la media di tutti gli elementi su cui si intende effettuare uno studio statistico.
Pertanto, la differenza tra la media campionaria e la media della popolazione è che la media campionaria è la media dei valori del campione, mentre la media della popolazione è la media dei valori della popolazione.
Per differenziare la media campionaria da quella della popolazione, queste sono rappresentate da simboli diversi. Il simbolo per la media del campione è
![]()
, mentre il simbolo della popolazione significa è
![]()
.
![Rendered by QuickLaTeX.com \begin{array}{c}\overline{x} = \text{Media muestral}\\[2ex]\mu =\text{Media poblacional}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e9047d35ec6ee8da3cb57e5134837876_l3.png)
La media campionaria viene utilizzata per stimare il valore della media della popolazione, operazione che può essere eseguita utilizzando la stima puntuale o la stima per intervallo .
Distribuzione campionaria delle medie campionarie
Infine, diamo un’occhiata a cosa significa distribuzione campionaria del campione, poiché è un concetto statistico che può creare confusione.
Innanzitutto, iniziamo definendo cos’è una distribuzione campionaria. Una distribuzione campionaria è la distribuzione che risulta dalla presa in considerazione di tutti i possibili campioni di una popolazione statistica.
Pertanto, la distribuzione campionaria della media campionaria è la distribuzione che risulta dal calcolo della media di ogni possibile campione di una popolazione. Cioè, se studiamo tutti i possibili campioni di una popolazione e calcoliamo la media di ciascuno dei campioni, l’insieme dei valori calcolati è una distribuzione campionaria della media campionaria.
In conclusione, sebbene la media campionaria e la distribuzione campionaria abbiano nomi simili, è necessario sapere come distinguerle: la media campionaria è un parametro statistico che si calcola a partire da un campione, una distribuzione campionaria è invece una distribuzione che risulta dallo studio di tutti i campioni che possono essere ricavati da una popolazione.