Come interpretare l'asimmetria in statistica: con esempi
In statistica, usiamo l’asimmetria per descrivere la simmetria di una distribuzione.
Diciamo che una distribuzione di valori di dati è distorta se ha una “coda” sul lato sinistro della distribuzione:
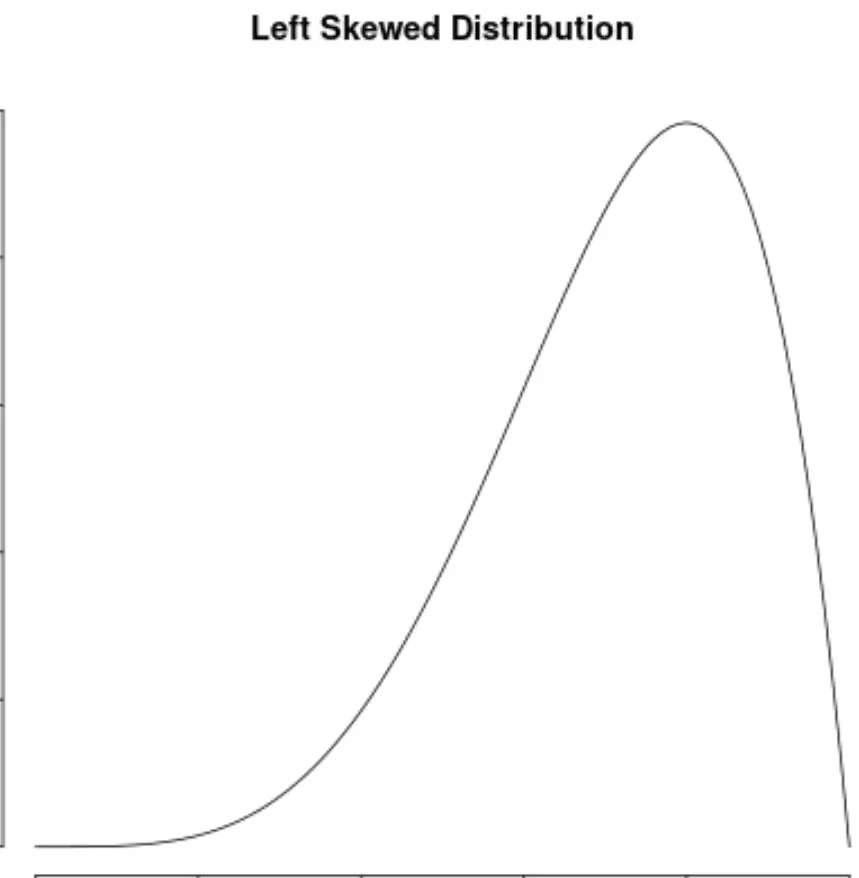
Una distribuzione si dice distorta a destra se ha una “coda” sul lato destro della distribuzione:
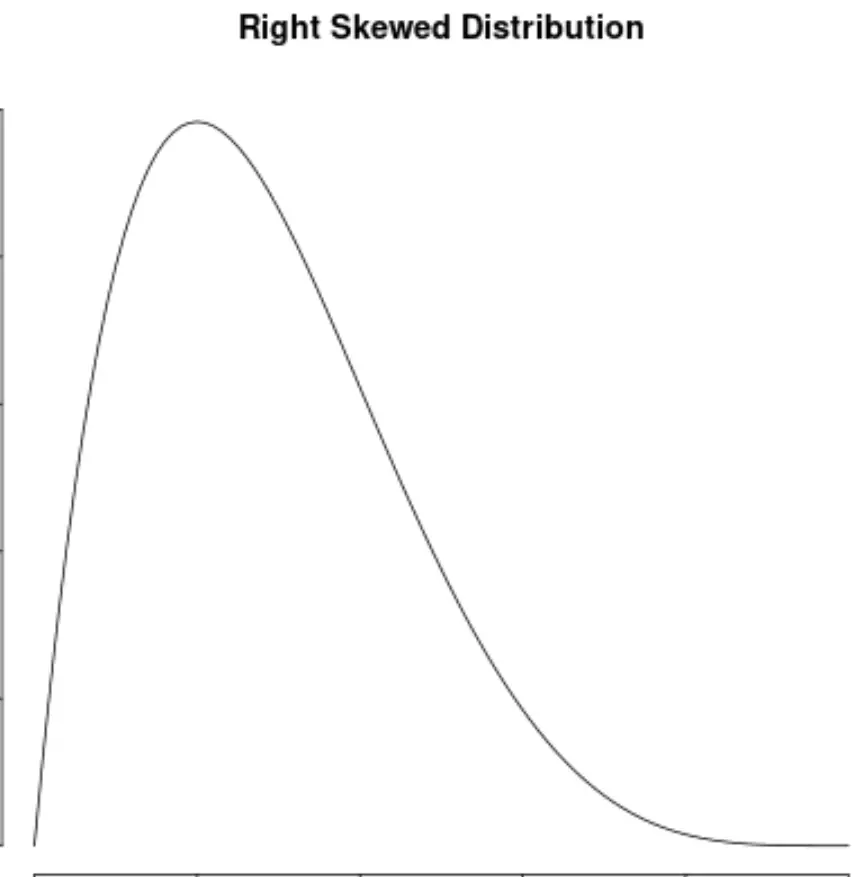
E diciamo che una distribuzione non ha asimmetria se è simmetrica su entrambi i lati:
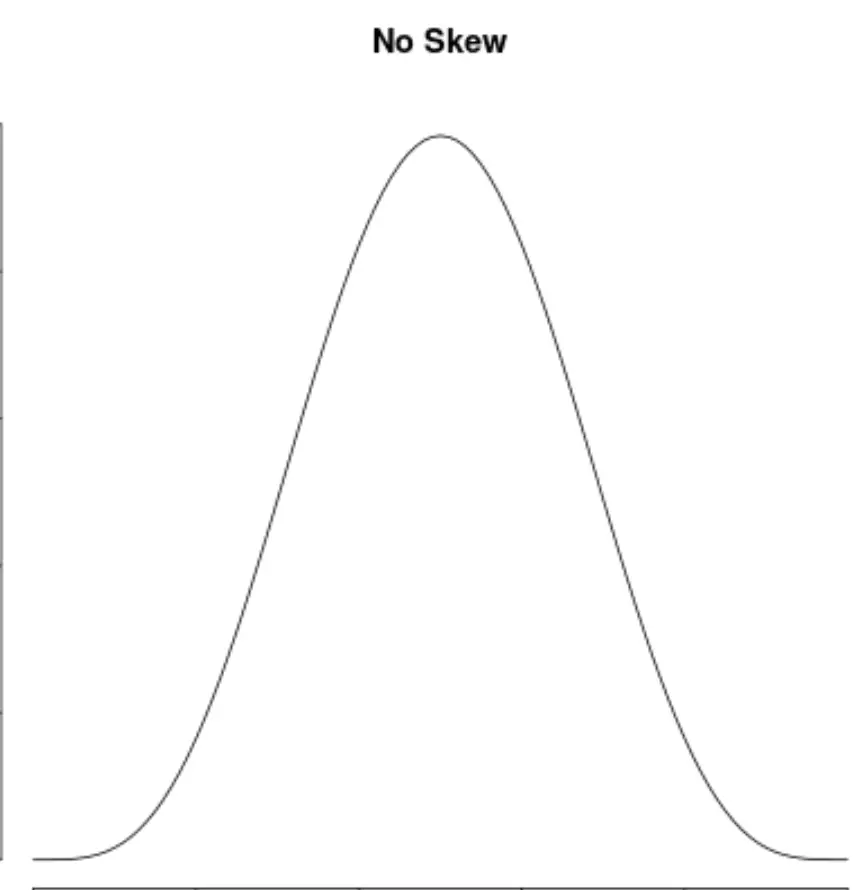
Come interpretare l’asimmetria
Il valore dell’asimmetria può variare da infinito negativo a infinito positivo.
Ecco come interpretare i valori di asimmetria:
- Un valore negativo per l’asimmetria indica che la coda si trova sul lato sinistro della distribuzione, che si estende verso valori più negativi.
- Un valore positivo per l’asimmetria indica che la coda si trova sul lato destro della distribuzione, che si estende verso valori più positivi.
- Un valore pari a zero indica che non c’è asimmetria nella distribuzione, il che significa che la distribuzione è perfettamente simmetrica.
Gli esempi seguenti mostrano come interpretare nella pratica i valori di asimmetria.
Esempio 1: distribuzione sbilanciata a sinistra
La distribuzione per età dei decessi nella maggior parte delle popolazioni è sbilanciata verso sinistra. La maggior parte delle persone vive tra i 70 e gli 80 anni, e sempre meno vivono al di sotto di questa età.
Se creassimo un grafico della densità per visualizzare la distribuzione dei valori per l’età della morte, potrebbe assomigliare a questo:
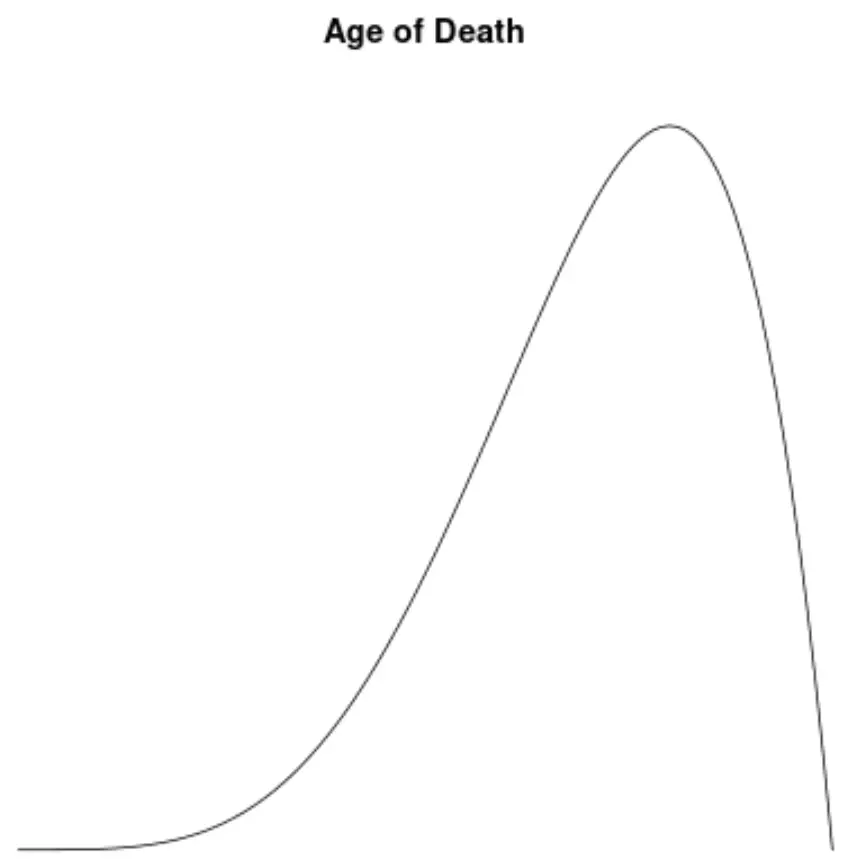
Supponiamo di calcolare l’asimmetria di questa distribuzione e di scoprire che è -1.3225 .
Poiché questo valore è negativo, lo interpretiamo nel senso che la distribuzione è distorta a sinistra, ovvero che la coda si estende verso il lato sinistro della distribuzione.
Esempio 2: distribuzione distorta a destra
La distribuzione del reddito familiare negli Stati Uniti è sbilanciata verso destra, con la maggior parte delle famiglie che guadagna tra i 30.000 e i 70.000 dollari all’anno, ma con una lunga coda destra di famiglie che guadagna molto di più.
Se creiamo un grafico della densità per visualizzare la distribuzione dei valori del reddito familiare, potrebbe assomigliare a questo:
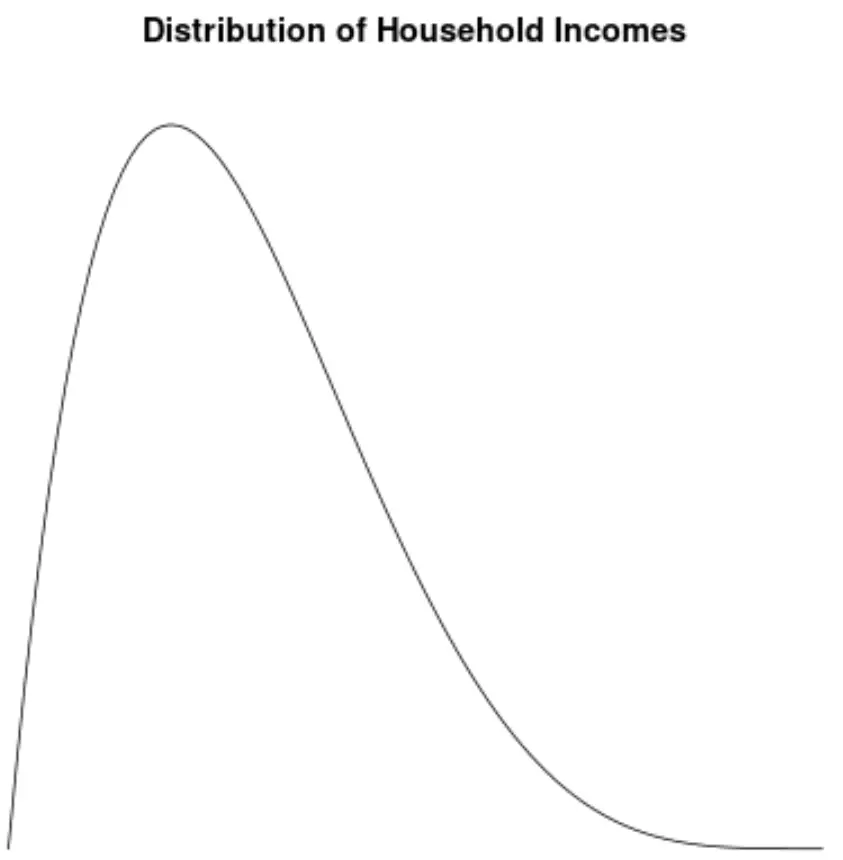
Supponiamo di calcolare l’asimmetria di questa distribuzione e di scoprire che è 2.0043 .
Poiché questo valore è positivo, lo interpretiamo nel senso che la distribuzione è distorta a destra, ovvero che la coda si estende verso il lato destro della distribuzione.
Esempio 3: nessun pregiudizio
La dimensione dei maschi è distribuita approssimativamente normalmente e non mostra asimmetria. Ad esempio, l’altezza media di un uomo negli Stati Uniti è di circa 69,1 pollici. La distribuzione dell’altezza è più o meno simmetrica, con alcuni più bassi e altri più alti.
Se creassimo un grafico della densità per visualizzare la distribuzione dell’altezza maschile negli Stati Uniti, potrebbe apparire così:
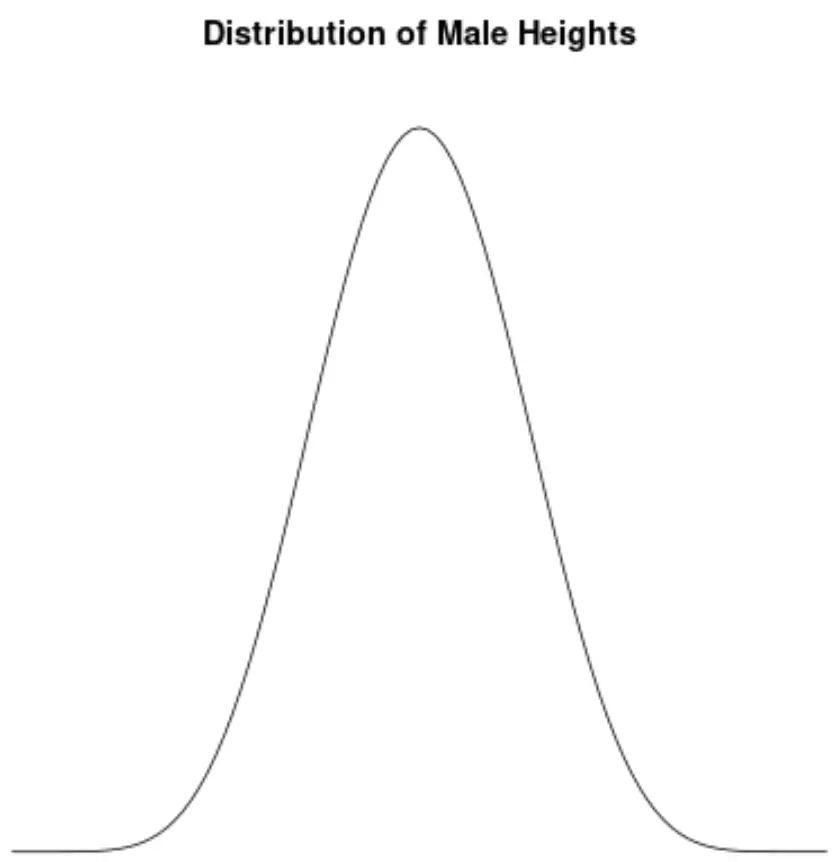
Supponiamo di calcolare l’asimmetria di questa distribuzione e di scoprire che è 0,0013 .
Poiché questo valore è vicino allo zero, lo interpretiamo nel senso che la distribuzione non ha praticamente alcuna distorsione, il che significa che le code su entrambi i lati della distribuzione sono approssimativamente uguali.
Risorse addizionali
Le seguenti esercitazioni forniscono informazioni aggiuntive sulle statistiche di distorsione:
5 esempi di distribuzioni asimmetriche positivamente
5 esempi di distribuzioni asimmetriche negativamente
Come calcolare l’asimmetria in Excel
Come identificare l’asimmetria nei box plot