Come leggere un box plot con valori anomali (con esempio)

Un box plot è un tipo di grafico che visualizza il riepilogo di cinque cifre di un set di dati, che include:

• Il valore minimo
• Il primo quartile (il 25° percentile)
• Il valore mediano
• Il terzo quartile (il 75° percentile)
• Il valore massimo

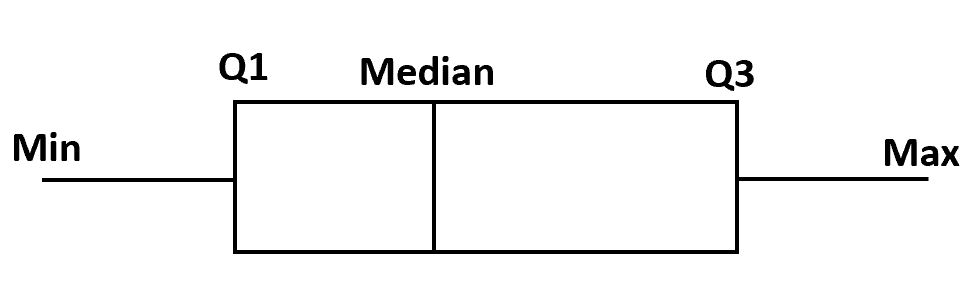
Per realizzare un box plot, disegniamo prima un riquadro dal primo al terzo quartile.

Successivamente, tracciamo una linea verticale in corrispondenza della mediana.

Infine disegniamo i “baffi” dei quartili fino al valore minimo e massimo.

Nella maggior parte dei software statistici, un’osservazione è definita outlier se soddisfa uno dei due requisiti seguenti:

• L’osservazione è 1,5 volte l’intervallo interquartile inferiore al primo quartile (Q1)
• L’osservazione è 1,5 volte l’intervallo interquartile sopra il terzo quartile (Q3).

Se in un set di dati esiste un valore anomalo, di solito viene etichettato con un piccolo punto all’esterno dell’intervallo dei baffi nel box plot:

Quando ciò accade, ai valori “minimo” e “massimo” nel boxplot vengono semplicemente assegnati rispettivamente i valori Q1 – 1,5*IQR e Q3 + 1,5*IQR.

L’esempio seguente mostra come interpretare i box plot con e senza valori anomali.

Esempio: interpretazione di un box plot con valori anomali

Supponiamo di creare i seguenti due box plot per visualizzare la distribuzione dei punti segnati dai giocatori di basket di due squadre diverse:

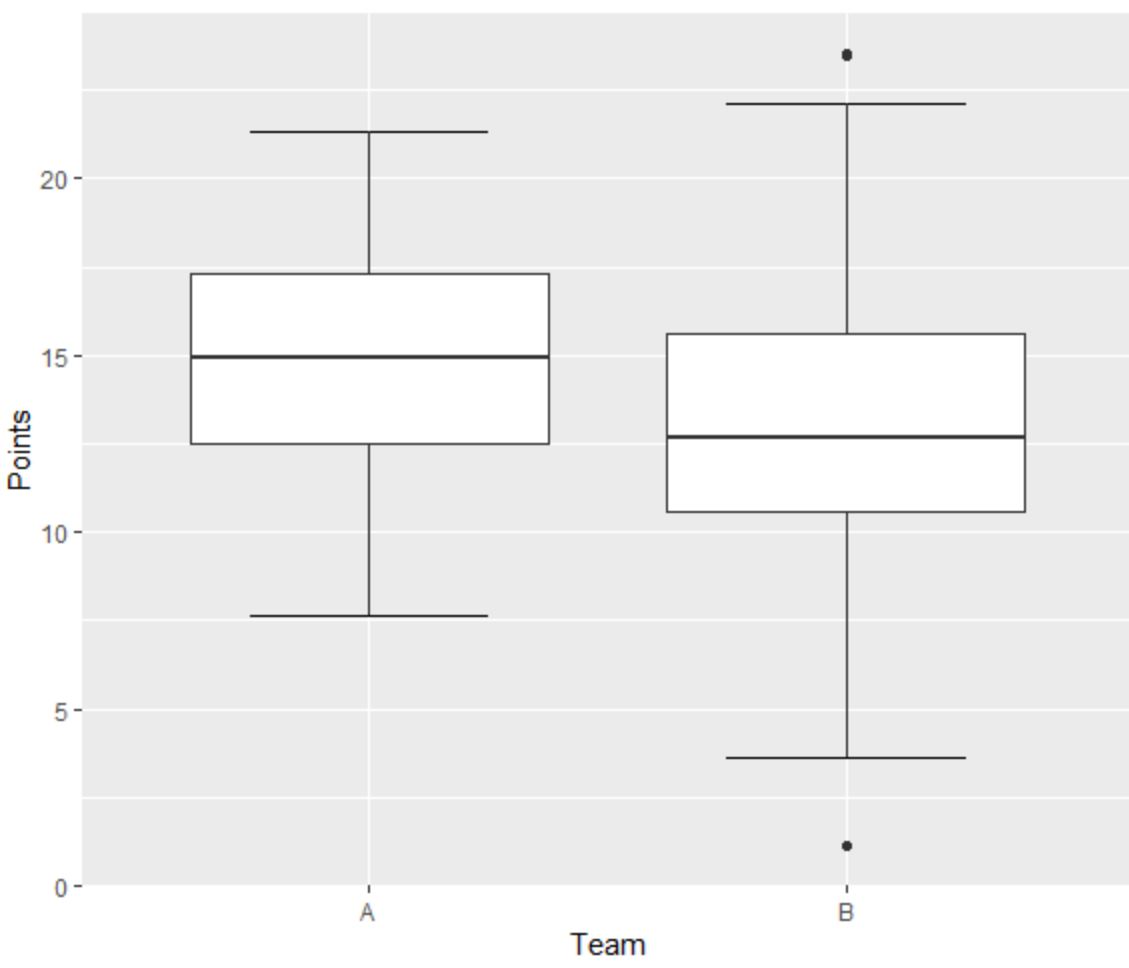
Il boxplot di sinistra per la squadra A non presenta valori anomali poiché non sono presenti piccoli punti situati al di fuori del baffo minimo o massimo.

Tuttavia, il boxplot corretto per la squadra B ha un valore anomalo sopra il valore “massimo” e un valore anomalo sotto il valore “minimo”.

Ecco l’attuale riepilogo a cinque cifre per la distribuzione della variabile “Punti” per la squadra B:

• Valore minimo: 1.1
• Primo quartile: 10,5
• Mediana: 12,7
• Terzo quartile: 15,6
• Valore massimo: 23,5

Ecco come calcolare i limiti dei potenziali valori anomali:

Scala interquartile : Terzo quartile – Primo quartile = 15,6 – 10,5 = 5,1

Limite inferiore : Q1 – 1,5*IQR = 10,5 – 1,5*5,1 = 2,85

Limite superiore : Q3 + 1,5*IQR = 15,6 + 1,5*5,1 = 23,25

I baffi per i valori minimo e massimo nel boxplot sono posizionati a 2,85 e 23,25 .

Pertanto, le osservazioni con valori pari a 1,1 e 23,5 si qualificano entrambe come valori anomali nel boxplot perché non rientrano nei limiti inferiore e superiore.

Bonus : ecco il codice esatto che abbiamo utilizzato per creare questi due boxplot nel linguaggio di programmazione R:

 library (ggplot2)

#make this example reproducible 
set. seeds (2)

#create data frame
df <- data. frame (Team = factor(rep(c("A", "B"), each = 200)), 
                 Points = c(rnorm(200, mean = 15, sd = 3), 
                           rnorm(200, mean = 12, sd = 4))) 

#create box plots
ggplot(df, aes(x = Team, y = Points)) +
  stat_boxplot(geom = " errorbar ", width = 0.5) +  
  geom_boxplot() 

#calculate summary statistics for each team
tapply(df$Points, df$Team, summary)

Risorse addizionali

Le seguenti esercitazioni forniscono informazioni aggiuntive sui box plot:

Come confrontare i box plot
Come identificare l’asimmetria nei box plot
Come trovare lo scarto interquartile di un boxplot