Scheda di controllo p
In questo articolo imparerai cosa sono le carte di controllo P e a cosa servono. Spieghiamo anche come costruire una carta di controllo P e, inoltre, potrai vedere un esercizio risolto passo dopo passo.
Cos’è una carta di controllo P?
Una carta di controllo P , o semplicemente carta P , è un grafico che rappresenta l’evoluzione della percentuale di unità difettose e dei loro limiti di controllo . Pertanto, una carta di controllo P è una carta utilizzata per controllare la proporzione di unità difettose.
Nella gestione della qualità spesso dobbiamo studiare se in un processo produttivo le unità sono realizzate correttamente o, al contrario, se si verificano troppi difetti. La carta di controllo P permette quindi di analizzare l’evoluzione della percentuale di unità difettose e di vedere quando il processo produttivo è sotto controllo e quando no.
Tuttavia, la carta di controllo P non viene utilizzata solo per controllare un processo di produzione, ma ha anche altre applicazioni come il controllo della proporzione di pazienti o il controllo del tasso di successo di un esperimento dicotomico. Sebbene sia utilizzato principalmente per controllare i processi produttivi.
Una delle caratteristiche della carta di controllo P è che la dimensione dei diversi campioni analizzati non deve necessariamente essere uguale, per cui è possibile prelevare campioni di dimensioni diverse per effettuare lo studio statistico.
In breve, la carta di controllo P permette di analizzare casi in cui ci sono due possibili esiti: “successo” (unità ben prodotta) e “fallimento” (unità difettosa). Cioè, la carta di controllo P è utile per i casi che seguono una distribuzione binomiale.
Come creare una carta di controllo P
Per creare una carta di controllo P è necessario seguire i seguenti passaggi:
- Prendi dei campioni : prima di tutto, devi prendere diversi campioni per vedere come cambia la proporzione nel grafico. I campioni possono essere di dimensioni diverse, ma si consiglia di prelevare un minimo di 20 campioni.
- Calcolare la proporzione p : Per ciascun campione, è necessario calcolare la proporzione di individui carenti.
- Calcolare il valore medio della proporzione : da tutti gli elementi studiati, è necessario calcolare la proporzione totale delle unità difettose.
- Calcolare i limiti di controllo della carta P : per ciascun campione analizzato, è necessario trovare i limiti di controllo utilizzando le formule fornite di seguito. Tieni presente che il valore dei limiti di controllo varierà se la dimensione di ciascun campione è diversa.
- Tracciare i valori sul grafico : ora è necessario tracciare sul grafico i valori delle proporzioni del campione ottenute nonché i limiti di controllo calcolati.
- Analizzare la carta di controllo P : infine non resta che verificare che nessun valore delle proporzioni superi i limiti di controllo e che il processo sia quindi sotto controllo. In caso contrario, è necessario adottare misure per correggere il processo di produzione.
![]()
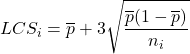
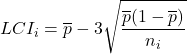
Oro
![]()
E
![]()
sono rispettivamente i limiti di controllo superiore e inferiore del campione i,
![]()
è il valore medio della proporzione di difetti e
![]()
è la dimensione del campione i.
Esempio di carta di controllo P
Per finire di assimilare il concetto, vedremo un esempio risolto di creazione di una carta di controllo P.
- Un’azienda ha raccolto 25 campioni di prodotti e ha registrato in ciascun campione la dimensione del campione e il numero di parti difettose trovate. Puoi vedere i dati raccolti nella seguente tabella:
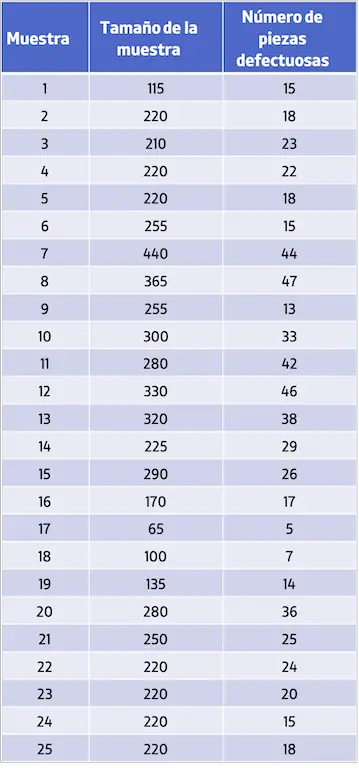
Per elaborare la carta di controllo P è necessario innanzitutto calcolare la proporzione totale delle unità difettose. Per fare ciò, dividi semplicemente il numero totale di difetti per il numero totale di unità prodotte:
![]()
Ora calcoliamo la proporzione dei difetti per ciascun campione e i limiti di controllo per ciascun campione. Ad esempio, procediamo al calcolo del primo campione:
![]()
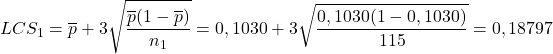
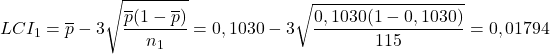
Pertanto, la proporzione dei difetti e i limiti di controllo per ciascun campione sono i seguenti:
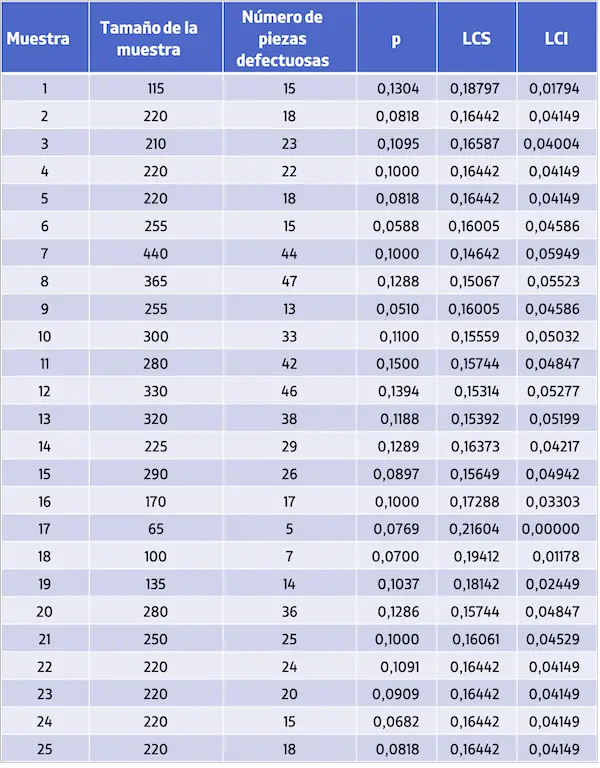
Una volta calcolati tutti i limiti di controllo, rappresentiamo su un grafico i valori delle proporzioni dei difetti e i relativi limiti di controllo per ottenere il grafico di controllo P:
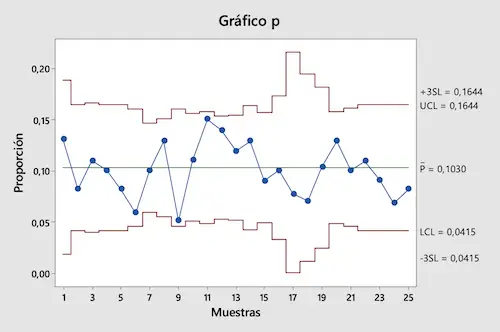
Come puoi vedere dal grafico, tutti i valori delle proporzioni rientrano nei limiti di controllo. Concludiamo quindi che il processo produttivo studiato è sotto controllo.
Altri tipi di carte di controllo
Il grafico P è un tipo di grafico di controllo degli attributi. Altre carte di controllo degli attributi esistenti includono:
- Carta di controllo NP – A differenza della carta P, non viene controllata la percentuale di prodotti difettosi, ma piuttosto il numero di prodotti difettosi.
- Scheda di controllo C : Viene monitorato il numero di guasti che si verificano.
- Carta di controllo U : il numero di difetti è controllato come nella carta C, ma la dimensione del campione è variabile.