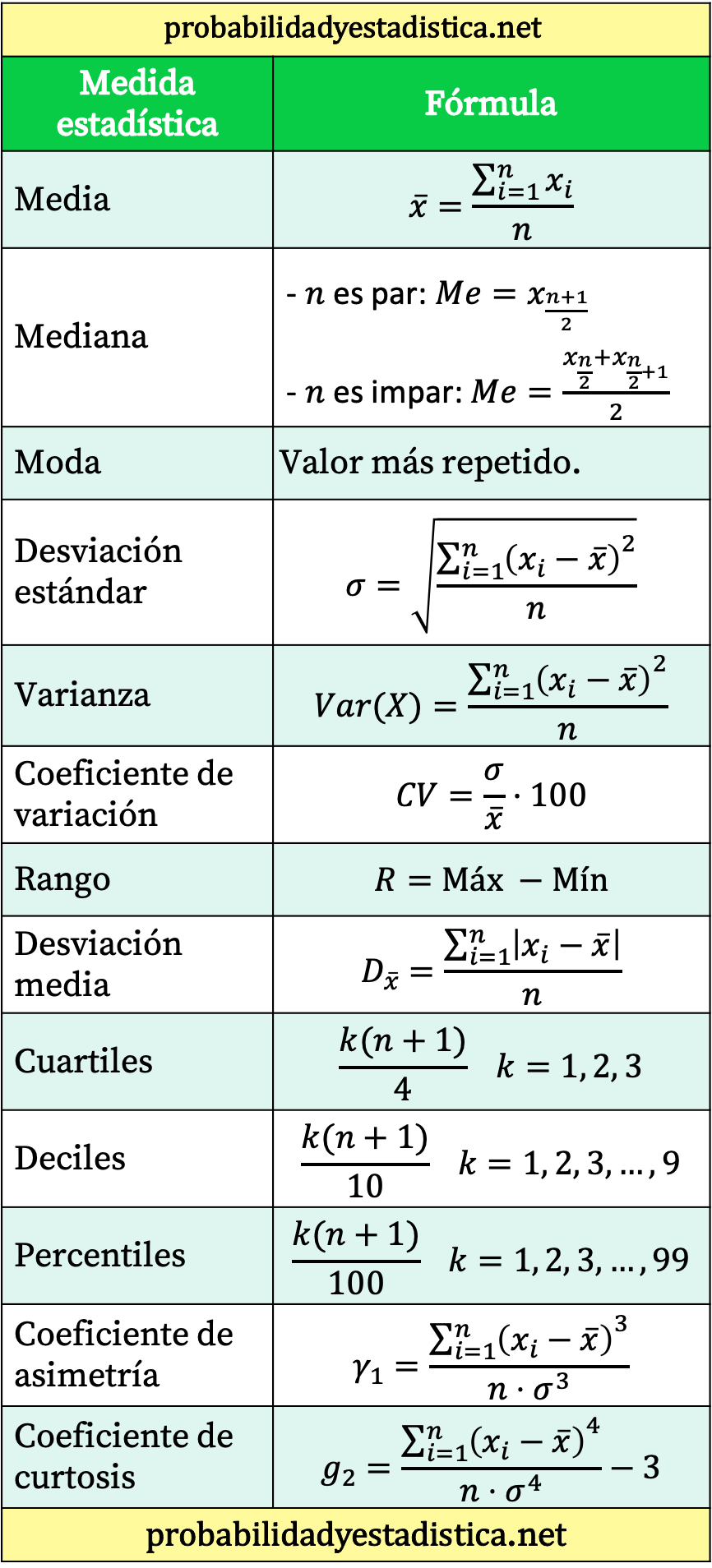
Formule statistiche

Di Benjamin anderson Agosto 1, 2023 Statistiche 0 commenti

Qui troverete le principali formule statistiche. Vi lasciamo anche collegati ai nostri articoli in cui potrete vedere esempi di applicazione di ciascuna formula statistica e, inoltre, potrete utilizzare un calcolatore online per non dover fare i calcoli e conoscere direttamente il risultato della formula.

Formule per misure statistiche di tendenza centrale

Metà

Per calcolare la media, somma tutti i valori e poi dividi per il numero totale di dati. La formula della media è quindi la seguente:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}$

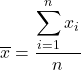
In statistica la media è detta anche media aritmetica o media .

➤ Vedi: Calcolatore della media aritmetica

Mediano

La mediana è il valore medio di tutti i dati ordinati dal più piccolo al più grande. In altre parole, la mediana divide il set di dati ordinato in due parti uguali.

Il calcolo della mediana dipende dal fatto che il numero totale di dati sia pari o dispari:

Se il numero totale di dati è dispari , la mediana sarà il valore che si trova proprio al centro dei dati. Vale a dire il valore che si trova nella posizione (n+1)/2 dei dati ordinati.

$Me=x_{\frac{n+1}{2}$

Se il numero totale di punti dati è pari , la mediana sarà la media dei due punti dati situati al centro. Vale a dire la media aritmetica dei valori che si trovano alle posizioni n/2 e n/2+1 dei dati ordinati.

$Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$

Oro

$n$

è il numero totale di dati nel campione e il simbolo Me indica la mediana.

➤ Vedi: Calcolatore della mediana

Moda

In statistica, la moda è il valore nel set di dati che ha la frequenza assoluta più alta, ovvero la moda è il valore più ripetuto in un set di dati.

Pertanto, non esiste una formula specifica per la moda, ma per calcolare la moda di un set di dati statistici, è sufficiente contare il numero di volte in cui ciascun elemento di dati appare nel campione e i dati più ripetuti saranno la moda.

Si può anche dire che la modalità è modalità statistica o valore modale .

➤ Vedi: Calcolatore della moda

Formule per misure statistiche di dispersione

Deviazione standard

La deviazione standard, chiamata anche deviazione standard, è uguale alla radice quadrata della somma dei quadrati delle deviazioni della serie di dati divisa per il numero totale di osservazioni.

Pertanto, la formula per la deviazione standard è:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n}}$

➤ Vedi: Calcolatore della deviazione standard

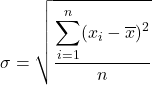
Varianza

La varianza è uguale alla somma dei quadrati dei residui sul numero totale di osservazioni. La formula per questa metrica statistica è quindi la seguente:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}$

Oro:

$X$

è la variabile casuale di cui si vuole calcolare la varianza.
$x_i$

è il valore dei dati

$i$

.
$n$

è il numero totale di osservazioni.
$\overline{X}$

è la media della variabile casuale

$X$

.

➤ Vedi: Calcolatore del gap

Coefficiente di variazione

In statistica, il coefficiente di variazione è una misura di dispersione utilizzata per determinare la dispersione di un insieme di dati rispetto alla sua media. Il coefficiente di variazione viene calcolato dividendo la deviazione standard dei dati per la sua media, quindi moltiplicando per 100 per esprimere il valore come percentuale.

$CV=\cfrac{\sigma}{\overline{x}}\cdot 100$

➤ Vedi: Calcolatore del coefficiente di variazione

Ordinato

L’intervallo statistico è una misura di dispersione che indica la differenza tra il valore massimo e il valore minimo dei dati in un campione. Pertanto, per calcolare l’entità di una popolazione o di un campione statistico, è necessario sottrarre il valore massimo dal valore minimo.

$R=\text{M\'ax}-\text{M\'in}$

➤ Vedi: Esempio di intervallo statistico

Intervallo interquartile

Lo scarto interquartile , chiamato anche scarto interquartile , è una misura di dispersione statistica che indica la differenza tra il terzo e il primo quartile.

Pertanto, per calcolare l’intervallo interquartile di un set di dati statistici, è necessario prima trovare il terzo e il primo quartile e poi sottrarli.

$IQR=Q_3-Q_1$

➤ Vedi: Calcolatore dell’intervallo interquartile

differenza media

La deviazione media , chiamata anche deviazione media assoluta , è la media delle deviazioni assolute. La deviazione media è quindi pari alla somma delle deviazioni di ciascun dato dalla media aritmetica divisa per il numero totale di dati.

$D_{\overline{x}}=\cfrac{\sum_{i=1}^n|x_i-\overline{x}|}{n}$

➤ Vedi: Calcolatore della deviazione media

Formule per le misurazioni statistiche della posizione

quartili

In statistica i quartili sono i tre valori che dividono un insieme di dati ordinati in quattro parti uguali. Pertanto, il primo, il secondo e il terzo quartile rappresentano rispettivamente il 25%, 50% e 75% di tutti i dati statistici.

I quartili sono rappresentati da una Q maiuscola e dall’indice quartile, quindi il primo quartile è Q ₁ , il secondo quartile è Q ₂ e il terzo quartile è Q ₃ .

La formula del quartile è:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

Nota: questa formula ci dice la posizione del quartile, non il valore del quartile. Il quartile saranno i dati situati nella posizione ottenuta dalla formula.

Tuttavia, a volte il risultato di questa formula ci darà un numero decimale. Dobbiamo quindi distinguere due casi a seconda che il risultato sia un numero decimale oppure no:

Se il risultato della formula è un numero senza parte decimale , il quartile è il dato che si trova nella posizione fornita dalla formula precedente.
Se il risultato della formula è un numero con una parte decimale , il valore quartile viene calcolato utilizzando la seguente formula:

$Q=x_i+d\cdot (x_{i+1}-x_i)$

Dove x _i e x _i+1 sono i numeri delle posizioni tra le quali si trova il numero ottenuto dalla prima formula, e d è la parte decimale del numero ottenuto dalla prima formula.

➤ Vedi: Calcolatore quartile

decili

In statistica i decili sono i nove valori che dividono un insieme di dati ordinati in dieci parti uguali. In modo che il primo, il secondo, il terzo,… decile rappresentino il 10%, 20%, 30%,… del campione o della popolazione.

I decili sono rappresentati dalla lettera maiuscola D e dall’indice del decile, ovvero il primo decile è D ₁ , il secondo decile è D ₂ , il terzo decile è D ₃ , ecc.

La formula del decile è la seguente:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9$

Nota: questa formula ci dice la posizione del decile, non il valore del decile. Il decile sarà il dato situato nella posizione ottenuta dalla formula.

Tuttavia, a volte il risultato di questa formula ci darà un numero decimale, dobbiamo quindi distinguere due casi a seconda che il risultato sia un numero decimale o meno:

Se il risultato della formula è un numero senza parte decimale , il decile è il dato situato nella posizione prevista dalla formula sopra.
Se il risultato della formula è un numero con parte decimale , il valore decile viene calcolato utilizzando la seguente formula:

$D=x_i+d\cdot (x_{i+1}-x_i)$

Dove x _i e x _i+1 sono i numeri delle posizioni tra le quali si trova il numero ottenuto dalla prima formula, e d è la parte decimale del numero ottenuto dalla prima formula.

➤ Vedi: Calcolatore dei decili

percentili

In statistica i percentili sono i valori che dividono un insieme di dati ordinati in cento parti uguali. Quindi, un percentile indica il valore al di sotto del quale cade una percentuale del set di dati.

I percentili sono rappresentati dalla lettera maiuscola P e dall’indice percentile, ovvero il primo percentile è P ₁ , il 40° percentile è P ₄₀ , il 79° percentile è P ₇₉ , ecc.

La formula percentile è:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

Nota: questa formula ci dice la posizione del percentile, ma non il suo valore. Il percentile saranno i dati situati nella posizione ottenuta dalla formula.

Tuttavia, a volte il risultato di questa formula ci darà un numero decimale, dobbiamo quindi distinguere due casi a seconda che il risultato sia un numero decimale o meno:

Se il risultato della formula è un numero senza parte decimale , il percentile corrisponde al dato che si trova nella posizione fornita dalla formula sopra.
Se il risultato della formula è un numero con una parte decimale , il valore percentile esatto viene calcolato utilizzando la seguente formula:

$P=x_i+d\cdot (x_{i+1}-x_i)$

Dove x _i e x _i+1 sono i numeri delle posizioni tra le quali si trova il numero ottenuto dalla prima formula, e d è la parte decimale del numero ottenuto dalla prima formula.

➤ Vedi: Calcolatore percentile

Formule di misurazione statistica della forma

coefficiente di asimmetria

Il coefficiente di asimmetria, o indice di asimmetria, è un coefficiente statistico utilizzato per determinare l’asimmetria di una distribuzione. Quindi, calcolando il coefficiente di asimmetria, è possibile conoscere il tipo di asimmetria della distribuzione senza doverne fare una rappresentazione grafica.

La formula per il coefficiente di asimmetria è la seguente:

$\displaystyle\gamma_1=\frac{\overline{x}_3}{\sigma^3}$

In modo equivalente, è possibile utilizzare una delle due formule seguenti per calcolare il coefficiente di asimmetria di Fisher:

$\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\overline{x}\right)^3}{n\cdot \sigma ^3}$

$\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\cdot \overline{x}\cdot \sigma^2 - \overline{x}^3}{\sigma^3}$

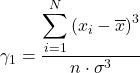
Oro

$E$

è l’aspettativa matematica,

$\overline{x}$

la media aritmetica,

$\sigma$

la deviazione standard e

$n$

il numero totale di dati.

➤ Vedi: Coefficiente di asimmetria

coefficiente di curtosi

La curtosi, detta anche nitidezza, indica quanto è concentrata una distribuzione attorno alla sua media. In altre parole, la curtosi indica se una distribuzione è ripida o piatta. Nello specifico, maggiore è la curtosi di una distribuzione, più ripida (o più nitida) è.

La formula per il coefficiente di curtosi è la seguente:

$\displaystyle g_2=\frac{1}{n}\cdot\frac{\displaystyle \sum_{i=1}^n(x_i-\overline{x})^4}{\sigma^4}-3$

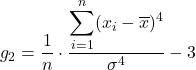
Oro

$x_i$

è il valore corrispondente all’osservazione

$i$

$\overline{x}$

la media aritmetica,

$\sigma$

la deviazione standard e

$n$

il numero totale di dati.

➤ Vedi: Calcolatore del coefficiente di appiattimento

Tabella riassuntiva di tutte le formule statistiche

Vi lasciamo infine una tabella che riassume le principali formule statistiche.

➤ Vedi: Formule di probabilità

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più

Formule per misure statistiche di tendenza centrale

Metà

Mediano

Moda

Formule per misure statistiche di dispersione

Deviazione standard

Varianza

Coefficiente di variazione

Ordinato

Intervallo interquartile

differenza media

Formule per le misurazioni statistiche della posizione

quartili

decili

percentili

Formule di misurazione statistica della forma

coefficiente di asimmetria

coefficiente di curtosi

Tabella riassuntiva di tutte le formule statistiche

Informazioni sull'autore

Benjamin anderson

Aggiungi un commento