Scheda di controllo u

Di Benjamin anderson Agosto 1, 2023 Gestione della qualità 0 commenti

In questo articolo ti spieghiamo cos’è una carta di controllo U, quali sono le sue caratteristiche e a cosa serve. Inoltre, potrai vedere come viene realizzata una carta di controllo U e come viene risolto un esercizio passo dopo passo.

Cos’è una carta di controllo U?

Una carta di controllo U , o semplicemente carta U , è un grafico che rappresenta il numero di volte in cui si verifica un fenomeno per unità di misura quando questa è variabile.

Ad esempio, è possibile utilizzare una carta di controllo U per controllare il numero di difetti per metro quadrato di tessuto. Spesso non è possibile prelevare campioni di tessuto con la stessa superficie, quindi ogni campione è diverso. Pertanto, il grafico U ci consente di studiare processi che hanno una dimensione campionaria variabile.

È importante notare che la carta di controllo U non rappresenta il numero di unità difettose, ma il numero di difetti che ciascuna unità ha, come nella carta C. Al contrario, una carta di controllo P o NP controlla la proporzione e il numero di prodotti difettosi. Di seguito esamineremo le differenze tra tutti i tipi di carte di controllo.

Tieni presente che il modello matematico di riferimento della carta di controllo U è la distribuzione di Poisson, poiché studiamo il numero di occorrenze di un fenomeno per unità di misura.

➤ Vedi: Distribuzione dei pesci

Come creare una carta di controllo U

Ora che conosciamo la definizione di carta di controllo U, vediamo come è realizzata questa tipologia di carta di controllo:

Prelievo dei campioni : in primo luogo è necessario prelevare diversi campioni per vedere l’evoluzione del fenomeno da misurare. I campioni devono essere della stessa dimensione, inoltre si consiglia di prelevare un minimo di 20 campioni.
Determinare il numero di volte in cui si verifica il fenomeno per unità di misura : per ciascun campione, quante volte si ripete il fenomeno da studiare.
Calcolare il valore medio degli eventi : dai dati raccolti è necessario calcolare la media dei tempi in cui si verifica il fenomeno per unità di misura.

$\overline{u}=\cfrac{\text{N\'umero de veces que ocurre el fen\'omeno}}{\text{N\'umero total de unidades de todas las muestras}}$

Calcolo dei limiti di controllo della U-Card – I limiti di controllo della U-Card devono quindi essere calcolati utilizzando le formule fornite di seguito. Tieni presente che il valore dei limiti di controllo varia a seconda della dimensione del campione.

$\displaystyle LCS_i=\overline{u}+3\sqrt{\frac{\overline{u}}{n_i}$

$\displaystyle LCI_i=\overline{u}-3\sqrt{\frac{\overline{u}}{n_i}$

Oro

$LCS_i$

$LCI_i$

sono rispettivamente i limiti di controllo superiore e inferiore del campione i,

$\overline{u}$

è il valore medio degli eventi e

$n_i$

è la dimensione del campione i.

Tracciamento dei valori sulla mappa – I valori raccolti insieme ai limiti di controllo calcolati devono ora essere tracciati su una mappa per creare la carta di controllo U.
Analizzare la carta di controllo U : in definitiva non resta che verificare che nessun valore presente sulla carta esca dai limiti di controllo e quindi che il processo sia sotto controllo. In caso contrario, è necessario adottare misure per correggere il processo.

Esempio di carta di controllo U

Un’azienda industriale desidera controllare il numero di difetti per ^m2 di tessuto. La tabella seguente presenta i campioni analizzati e il numero di difetti riscontrati. Crea una carta di controllo U per studiare il numero di difetti.

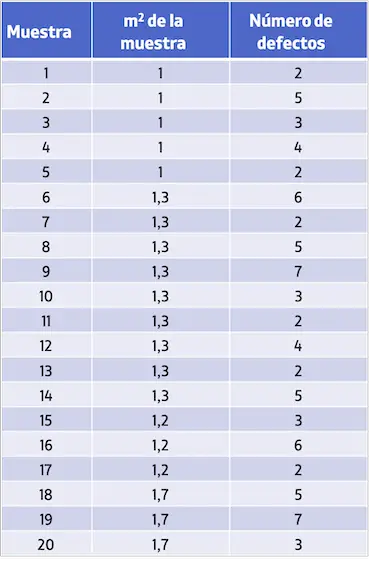
Per creare la carta di controllo U è necessario innanzitutto calcolare il valore medio del numero di difetti per campione:

$\overline{u}=\cfrac{\text{N\'umero de veces que ocurre el fen\'omeno}}{\text{N\'umero total de unidades}}=\cfrac{78}{25,4}=3,07$

Ora dobbiamo calcolare i limiti di controllo per ciascun campione. Ad esempio, i limiti di controllo per il primo campione sono calcolati di seguito:

$\displaystyle LCS_1=\overline{u}+3\sqrt{\frac{\overline{u}}{n_1}}=3,07+3\sqrt{\frac{3,07}{1}}=8,33$

$\displaystyle LCI_1=\overline{u}-3\sqrt{\frac{\overline{u}}{n_1}}=3,07-3\sqrt{\frac{3,07}{1}}=-2,19$

Tutti i limiti di controllo inferiori danno come risultato un numero negativo, il che non ha senso. Pertanto, imposteremo i limiti di controllo inferiori su 0.

Pertanto, i valori dei limiti di controllo per ciascun campione sono i seguenti:

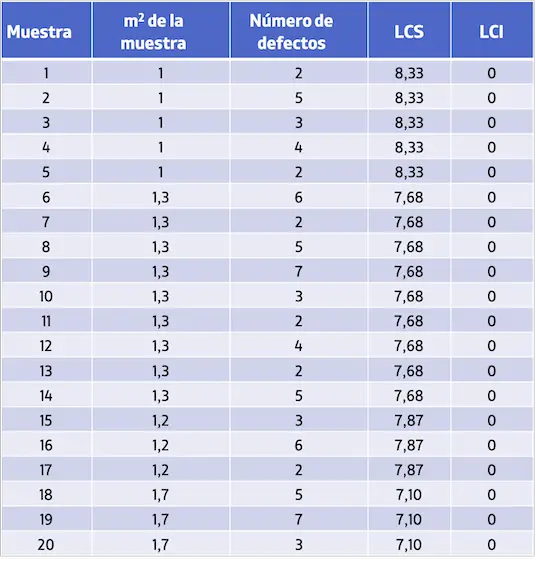
Infine è sufficiente rappresentare tutti i valori in un grafico per ottenere la carta di controllo U:

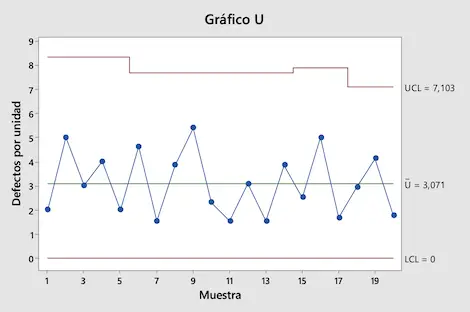
Come puoi vedere nel grafico U che abbiamo realizzato, tutti i valori sono compresi tra i limiti di controllo. Possiamo quindi concludere che il processo produttivo è sotto controllo.

Altri tipi di carte di controllo

Oltre alla carta U, esistono altri tipi di carte di controllo degli attributi:

Scheda di controllo P : viene controllata la percentuale di prodotti difettosi.
Scheda di controllo NP : viene controllato il numero di prodotti difettosi.
Carta di controllo C : il numero di difetti è controllato come nella carta U, ma la dimensione del campione è costante.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più