Come interpretare un grafico dei residui curvi (con esempio)
I grafici dei residui vengono utilizzati per valutare se i residui di un modello di regressione sono distribuiti normalmente e se presentano o meno eteroschedasticità .
Idealmente, si vorrebbe che i punti in un grafico residuo fossero sparsi in modo casuale attorno a un valore pari a zero, senza uno schema chiaro.
Se incontri un grafico residuo in cui i punti del grafico hanno uno schema curvo, probabilmente significa che il modello di regressione specificato per i dati non è corretto.
Nella maggior parte dei casi, ciò significa che si è tentato di adattare un modello di regressione lineare a un set di dati che segue invece un trend quadratico.
L’esempio seguente mostra come interpretare (e correggere) nella pratica un diagramma residuo curvo.
Esempio: interpretazione di un grafico dei residui curvo
Supponiamo di raccogliere i seguenti dati sul numero di ore lavorate settimanalmente e sul livello di felicità riportato (su una scala da 0 a 100) per 11 persone diverse in un ufficio:

Se creassimo un semplice grafico a dispersione delle ore lavorate rispetto al livello di felicità, ecco come apparirebbe:
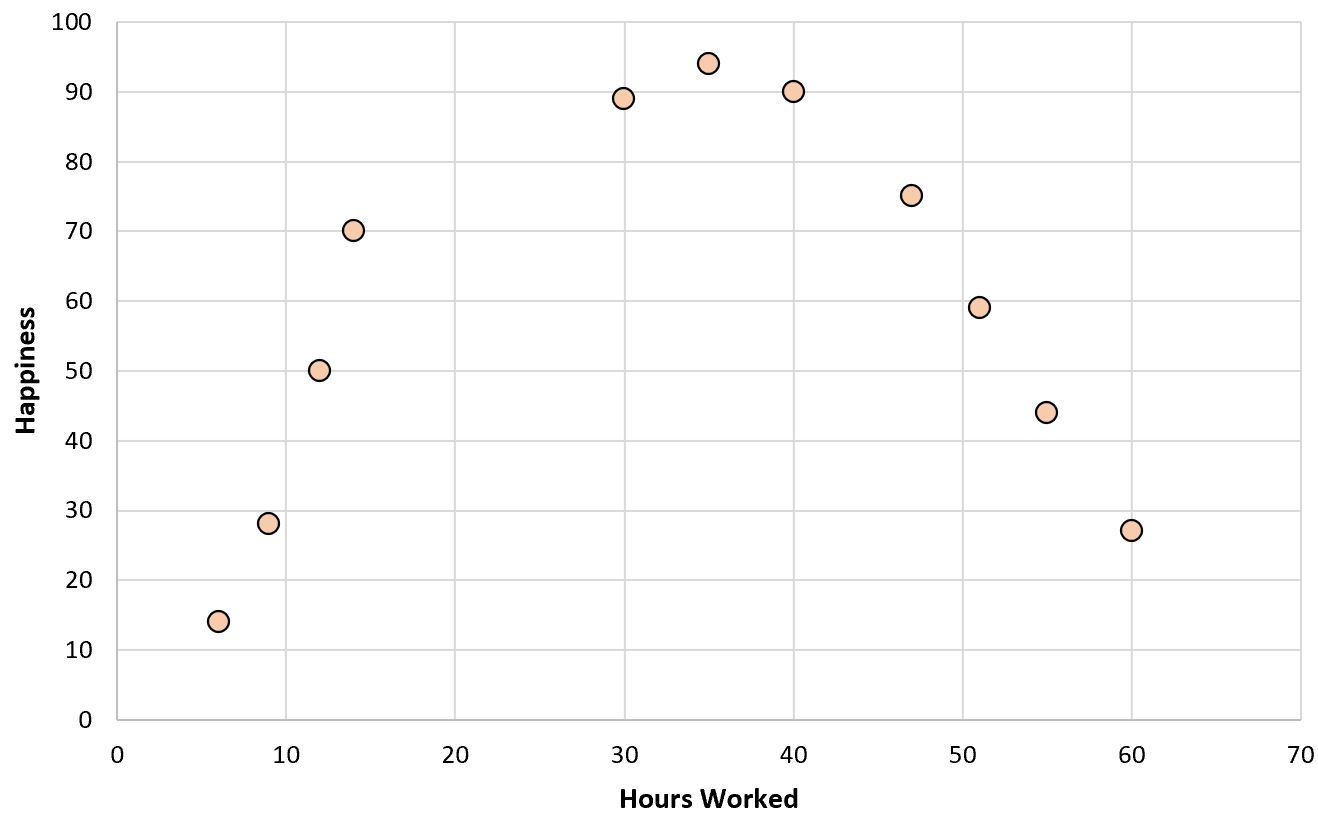
Supponiamo ora di voler adattare un modello di regressione utilizzando le ore lavorate per prevedere i livelli di felicità.
Il codice seguente mostra come adattare un modello di regressione lineare semplice a questo set di dati e produrre un grafico dei residui in R:
#create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#fit linear regression model
linear_model <- lm(happiness ~ hours, data=df)
#get list of residuals
res <- resid(linear_model)
#produce residual vs. fitted plot
plot(fitted(linear_model), res, xlab=' Fitted Values ', ylab=' Residuals ')
#add a horizontal line at 0
abline(0,0)
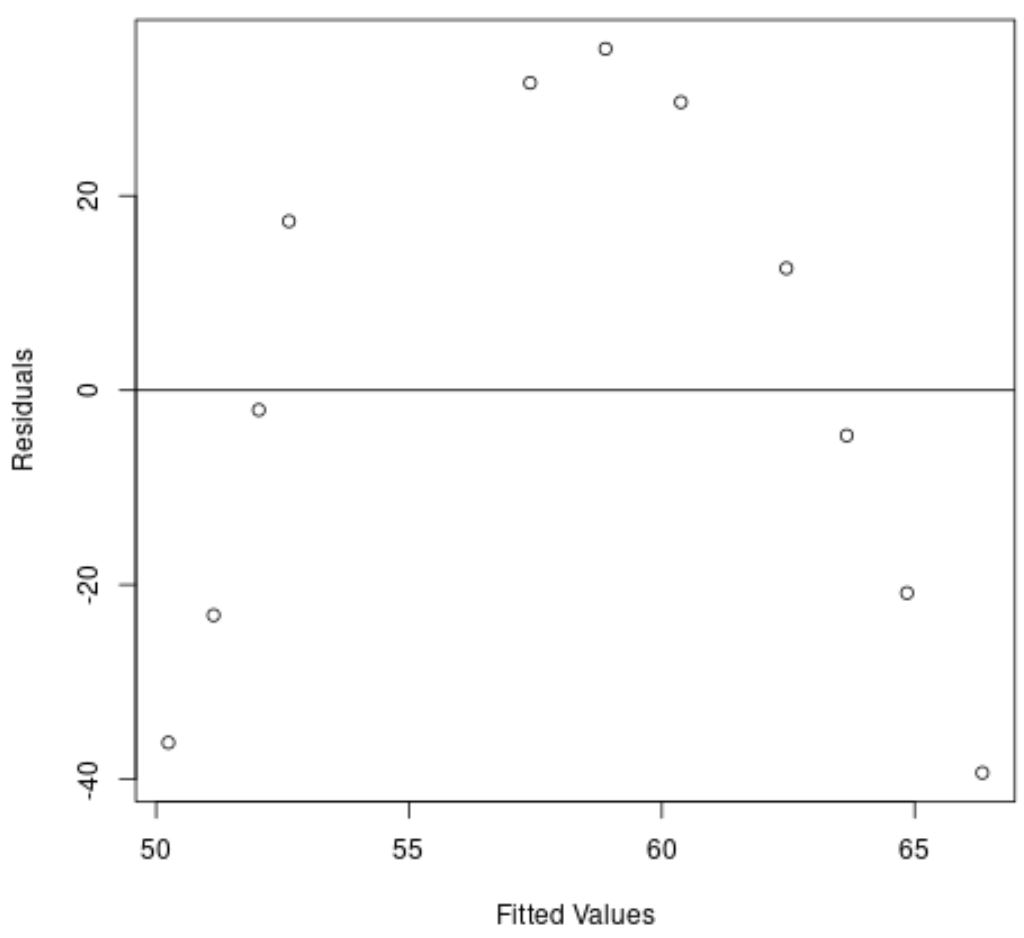
L’asse x mostra i valori adattati e l’asse y mostra i residui.
Dal grafico, possiamo vedere che esiste uno schema curvo nei residui, indicando che un modello di regressione lineare non fornisce un adattamento adeguato a questo set di dati.
Il codice seguente mostra come adattare un modello di regressione quadratica a questo set di dati e produrre un grafico dei residui in R:
#create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#define quadratic term to use in model
df$hours2 <- df$hours^2
#fit quadratic regression model
quadratic_model <- lm(happiness ~ hours + hours2, data=df)
#get list of residuals
res <- resid(quadratic_model)
#produce residual vs. fitted plot
plot(fitted(quadratic_model), res, xlab=' Fitted Values ', ylab=' Residuals ')
#add a horizontal line at 0
abline(0,0)
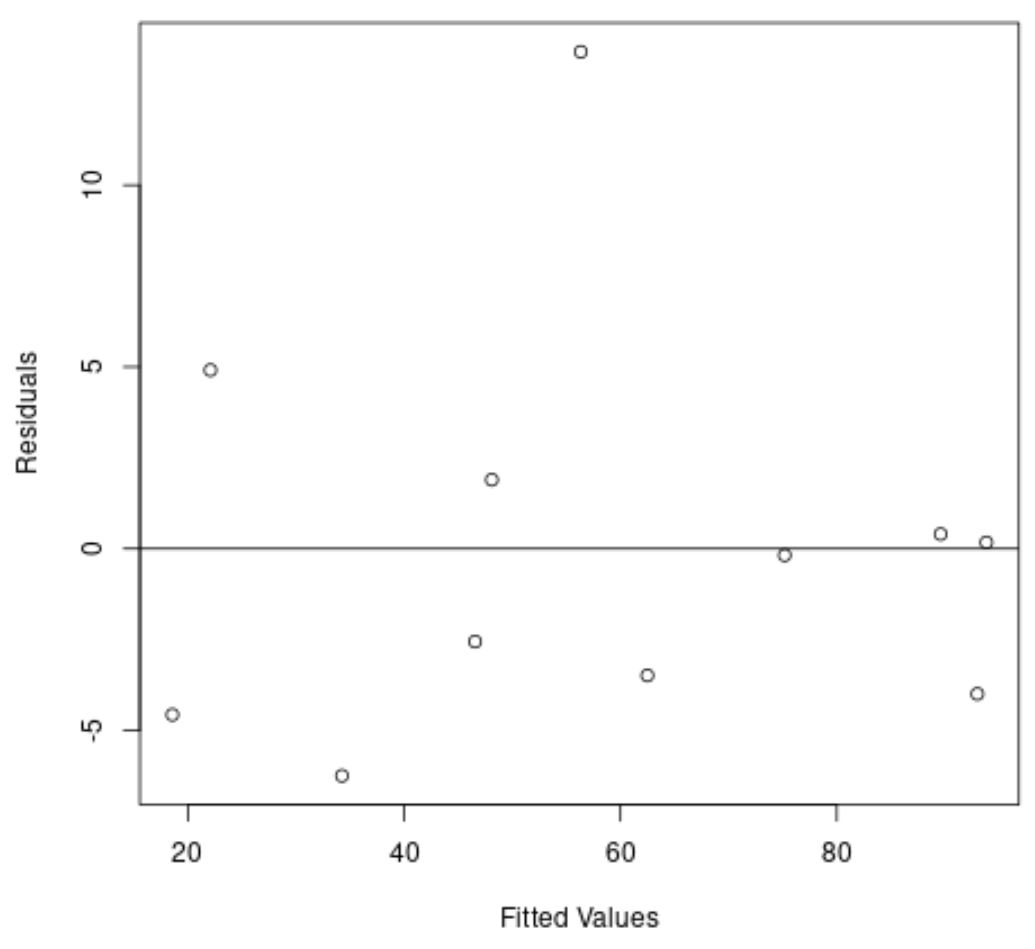
Ancora una volta, l’asse x mostra i valori adattati e l’asse y mostra i residui.
Dal grafico possiamo vedere che i residui sono sparsi in modo casuale attorno allo zero e non esiste una tendenza chiara nei residui.
Questo ci dice che un modello di regressione quadratica fa un lavoro molto migliore nell’adattare questo set di dati rispetto a un modello di regressione lineare.
Ciò dovrebbe avere senso dato che abbiamo visto che la vera relazione tra le ore lavorate e i livelli di felicità sembrava essere quadratica piuttosto che lineare.
Risorse addizionali
I seguenti tutorial spiegano come creare grafici dei residui utilizzando diversi software statistici:
Come creare manualmente un percorso residuo
Come creare una trama residua in R
Come creare un grafico residuo in Excel
Come creare un grafico residuo in Python