Probabilità condizionata (o probabilità condizionata)

Qui scoprirai cos’è la probabilità condizionata (o probabilità condizionata). Spieghiamo come viene calcolata la probabilità condizionata con un esempio e le proprietà di questo tipo di probabilità. Inoltre, potrai esercitarti con esercizi di probabilità condizionale risolti passo dopo passo.

Cos’è la probabilità condizionata?

La probabilità condizionata , detta anche probabilità condizionale , è una misura statistica che indica la probabilità che si verifichi l’evento A se si verifica un altro evento B. Cioè, la probabilità condizionata P(A|B) si riferisce alla probabilità che l’evento A si verifichi dopo che l’evento B si è già verificato.

La probabilità condizionata si scrive con una barra verticale tra i due eventi: P(A|B), e si legge: “la probabilità condizionata dell’evento A dato l’evento B”.

Si noti che il valore della probabilità condizionata è un numero compreso tra 0 e 1. Maggiore è la probabilità condizionata, maggiore è la probabilità che l’evento A si verifichi quando si verifica l’evento B, ma minore è la probabilità condizionata, minore è la probabilità che l’evento A si verifichi. accadrà quando si verificherà l’evento B.

Formula della probabilità condizionata

La probabilità condizionata dell’evento A dato l’evento B è uguale alla probabilità dell’intersezione tra l’evento A e l’evento B divisa per la probabilità dell’evento B.

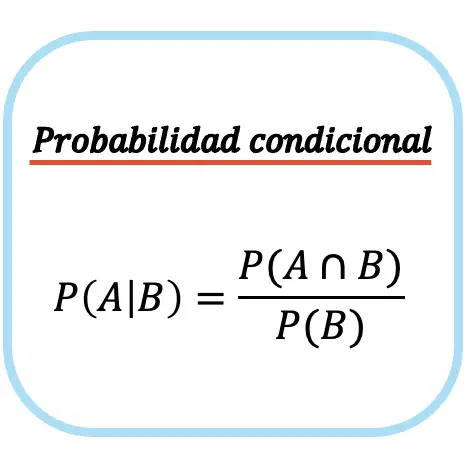
Si noti che la formula della probabilità condizionata (o probabilità condizionata) può essere utilizzata solo se la probabilità di accadimento dell’evento incondizionato è diversa da zero, ovvero P(B)≠0. O in altre parole, se è possibile che si verifichi l’evento B.

La probabilità condizionata può anche essere calcolata dal suo inverso, cioè se P(B|A) è noto, P(A|B) può essere determinato. Ma per fare questo devi applicare il teorema di Bayes, puoi vedere in cosa consiste questo teorema qui:

Esempio di probabilità condizionata

Una volta che abbiamo visto qual è la definizione e la formula della probabilità condizionata, risolveremo passo dopo passo un esempio di questo tipo di probabilità per comprenderne appieno il significato.

• Dopo aver sostenuto un esame in una classe di 30 studenti, sono stati raccolti dati per scoprire quanti studenti hanno studiato e quanti hanno superato l’esame. I risultati sono presentati nella seguente tabella di contingenza. Dai dati raccolti, calcola la probabilità condizionata di superare un esame se hai già studiato.

Per ottenere la probabilità condizionata dobbiamo applicare la formula che abbiamo visto in precedenza:

Pertanto, dobbiamo prima trovare la probabilità che uno studente abbia studiato, studiato e superato. Per trovare la probabilità che uno studente abbia studiato, dobbiamo semplicemente usare la regola di Laplace, ovvero dividere il numero di studenti che hanno studiato per il numero totale di osservazioni:

E possiamo scoprire la probabilità che uno studente abbia studiato e superato contemporaneamente dalla tabella di contingenza dividendo il numero di studenti che hanno studiato e superato per il totale:

Pertanto, la probabilità che uno studente superi un esame se ha studiato è:

Probabilità condizionata di eventi dipendenti e indipendenti

In questa sezione vedremo quale è la relazione tra probabilità condizionata ed eventi dipendenti e indipendenti (o eventi dipendenti e indipendenti). Perché, nonostante siano concetti diversi, questi due tipi di eventi sono legati ad una probabilità condizionata.

Due eventi (o occorrenze) sono indipendenti quando la loro probabilità di accadimento non dipende l’una dall’altra. In tal caso, l’intersezione tra i due eventi è equivalente al prodotto della probabilità di ciascun evento separatamente. E, quindi, la formula della probabilità condizionata è semplificata:

In breve, se gli eventi A e B sono indipendenti, la probabilità condizionata dell’evento A dato l’evento B è esattamente uguale alla probabilità che si verifichi l’evento A.

D’altra parte, quando due eventi sono dipendenti, significa che la probabilità di un evento dipende dalla probabilità dell’altro evento. Pertanto, quando due eventi A e B sono dipendenti, la probabilità condizionata dell’evento A dato l’evento B è diversa dalla probabilità che si verifichi l’evento A.

Esercizi di probabilità condizionata risolti

Esercizio 1

Sappiamo che in un sacchetto pieno di palline, metà è arancione e l’altra metà è verde. Inoltre un terzo di tutte le palline sono arancioni e allo stesso tempo contrassegnate da un cartello. Qual è la probabilità che quando si estrae una pallina arancione questa riceva il segnale?

Per risolvere l’esercizio dobbiamo applicare la formula condizionale della probabilità, che è:

La formulazione del problema ci dice che metà del sacchetto è costituito da arance. Pertanto, la probabilità teorica di raccogliere una pallina arancione è del 50%.

D’altra parte, sappiamo che un terzo del totale sono palline arancioni e hanno un segnale, quindi la probabilità di ottenere una pallina arancione con un segnale è:

Infine, sostituiamo le probabilità calcolate nella formula della probabilità condizionata per trovarne il valore:

In sintesi, la probabilità di estrarre una pallina con il segnale se è arancione è del 66%.

Esercizio 2

Se in una scatola abbiamo sei penne blu e tre penne nere, calcoliamo la probabilità di estrarre una singola penna blu e la probabilità di estrarre due penne blu consecutivamente.

Per determinare la probabilità di prendere in mano una penna blu una volta, utilizza semplicemente la legge di Laplace:

Il problema ci chiede anche di conoscere la probabilità di prendere in mano due penne blu consecutivamente, cioè la probabilità condizionata di prendere in mano una penna blu se abbiamo già preso in mano una penna blu in precedenza.

Se disegniamo una penna blu abbiamo un caso meno favorevole, ma c’è anche una penna in meno nel totale. La probabilità condizionata è quindi:

Esercizio 3

Qual è la probabilità condizionata che lanciando un dado esca il numero 4, dato che il lancio di una moneta dà testa?

Per risolvere questo esercizio, devi prendere in considerazione la teoria della probabilità condizionata, perché gli eventi “ottenere il numero 4 lanciando un dado” e “ottenere testa lanciando una moneta” sono indipendenti. Non è quindi necessario utilizzare la formula della probabilità condizionata, ma è soddisfatta la seguente uguaglianza:

Quindi, per trovare la probabilità condizionata, usa semplicemente la regola di Laplace:

Esercizio 4

È stato studiato l’anno finanziario di 25 società di un paese e come cambiano i prezzi delle loro azioni a seconda del risultato economico dell’anno. È possibile visualizzare i dati raccolti nella seguente tabella di contingenza:

Con quale probabilità il prezzo delle azioni di una società aumenta se ha realizzato un profitto nell’ultimo anno?

L’esercizio ci interroga sulla probabilità condizionata che le azioni salgano dato che la società ha raggiunto un risultato economico positivo. Quindi, per calcolare questa probabilità, dobbiamo usare la formula della probabilità condizionata:

Calcoliamo quindi prima la probabilità che un’azienda realizzi un profitto e, in secondo luogo, la probabilità che un’azienda realizzi un profitto economico aumentando il prezzo delle sue azioni:

E poi sostituiamo i valori trovati nella formula e calcoliamo la probabilità condizionale:

Proprietà della probabilità condizionata

Le proprietà della probabilità condizionata, o probabilità condizionata, sono le seguenti:

• La somma della probabilità condizionata dell’evento A dato l’evento B più la probabilità condizionata dell’evento complementare A dato l’evento B è uguale a uno.

• Se l’evento A è un sottoinsieme dell’evento B, A si verificherà sempre quando B è vero. Pertanto, la probabilità condizionata dell’evento A dato l’evento B in questi casi è 1.

• Dati due eventi diversi, vale sempre la seguente uguaglianza rispetto alla probabilità condizionata: