Introduzione alla regressione lineare semplice

La regressione lineare semplice è un metodo statistico che è possibile utilizzare per comprendere la relazione tra due variabili x e y.

Una variabile, x , è nota come variabile predittrice .

L’altra variabile, y , è nota come variabile di risposta .

Ad esempio, supponiamo di avere il seguente set di dati con il peso e l’altezza di sette individui:

Sia il peso la variabile predittrice e l’ altezza la variabile di risposta.

Se rappresentiamo graficamente queste due variabili utilizzando un grafico a dispersione, con il peso sull’asse x e l’altezza sull’asse y, ecco come apparirebbe:

Supponiamo di voler comprendere la relazione tra peso e altezza. Dal grafico a dispersione possiamo vedere chiaramente che all’aumentare del peso, anche l’altezza tende ad aumentare, ma per quantificare effettivamente questa relazione tra peso e altezza dobbiamo utilizzare la regressione lineare.

Usando la regressione lineare, possiamo trovare la linea che meglio “si adatta” ai nostri dati. Questa linea è nota come retta di regressione dei minimi quadrati e può essere utilizzata per aiutarci a comprendere la relazione tra peso e altezza.

Di solito, utilizzerai software come Microsoft Excel, SPSS o una calcolatrice grafica per trovare l’equazione per questa linea.

La formula per la retta di miglior adattamento è scritta:

ŷ = b ₀ + b ₁ x

dove ŷ è il valore previsto della variabile di risposta, b ₀ è l’intercetta, b ₁ è il coefficiente di regressione e x è il valore della variabile predittrice.

Correlati: 4 esempi di utilizzo della regressione lineare nella vita reale

Trova la “linea più adatta”

Per questo esempio, possiamo semplicemente inserire i nostri dati nel calcolatore di regressione lineare statistica e premere Calcola :

La calcolatrice trova automaticamente la retta di regressione dei minimi quadrati :

ŷ = 32,7830 + 0,2001x

Se rimpiccioliamo dal grafico a dispersione precedente e aggiungiamo questa linea al grafico, ecco come apparirebbe:

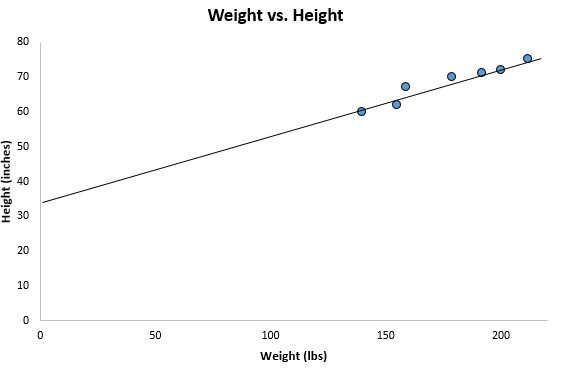
Nota come i nostri punti dati sono strettamente sparsi attorno a questa linea. In effetti, questa linea di regressione dei minimi quadrati è la linea più adatta ai nostri dati tra tutte le possibili linee che potremmo tracciare.

Come interpretare una retta di regressione dei minimi quadrati

Ecco come interpretare questa retta di regressione dei minimi quadrati: ŷ = 32,7830 + 0,2001x

_b0 = 32,7830 . Ciò significa che quando il peso della variabile predittore è pari a zero libbre, l’altezza prevista è 32,7830 pollici. A volte può essere utile conoscere il valore di b ₀ , ma in questo esempio specifico non ha senso interpretare b ₀ poiché una persona non può pesare zero chili.

_b1 = 0,2001 . Ciò significa che un aumento di un’unità di x è associato a un aumento di 0,2001 unità di y . In questo caso, un aumento di peso di una libbra è associato ad un aumento di altezza di 0,2001 pollici.

Come utilizzare la retta di regressione dei minimi quadrati

Utilizzando questa retta di regressione dei minimi quadrati, possiamo rispondere a domande come:

Per qualcuno che pesa 170 libbre, quanto dovremmo aspettarci che sia alto?

Per rispondere a questa domanda, possiamo semplicemente inserire 170 nella nostra retta di regressione per x e risolvere per y:

ŷ = 32,7830 + 0,2001(170) = 66,8 pollici

Per qualcuno che pesa 150 libbre, quanto dovremmo aspettarci che sia alto?

Per rispondere a questa domanda, possiamo inserire 150 nella nostra retta di regressione per x e risolvere per y:

ŷ = 32,7830 + 0,2001(150) = 62,798 pollici

Attenzione: quando si utilizza un’equazione di regressione per rispondere a domande come queste, assicurarsi di utilizzare solo valori per la variabile predittrice che rientrano nell’intervallo della variabile predittiva nel set di dati. origine che abbiamo utilizzato per generare la retta di regressione dei minimi quadrati. Ad esempio, i pesi nel nostro set di dati erano compresi tra 140 e 212 libbre. Quindi ha senso rispondere a domande sull’altezza prevista quando il peso è compreso tra 140 e 212 libbre.

Il coefficiente di determinazione

Un modo per misurare quanto bene la retta di regressione dei minimi quadrati “si adatta” ai dati è utilizzare il coefficiente di determinazione , indicato con R ² .

Il coefficiente di determinazione è la proporzione della varianza nella variabile di risposta che può essere spiegata dalla variabile predittore.

Il coefficiente di determinazione può variare da 0 a 1. Un valore pari a 0 indica che la variabile di risposta non può essere spiegata affatto dalla variabile predittrice. Un valore pari a 1 indica che la variabile di risposta può essere spiegata perfettamente senza errori dalla variabile predittore.

Un R ² compreso tra 0 e 1 indica la misura in cui la variabile di risposta può essere spiegata dalla variabile predittrice. Ad esempio, un ^R2 pari a 0,2 indica che il 20% della varianza nella variabile di risposta può essere spiegato dalla variabile predittore; un ^R2 di 0,77 indica che il 77% della varianza nella variabile di risposta può essere spiegato dalla variabile predittore.

Si noti che nel nostro risultato precedente abbiamo ottenuto un R ² di 0,9311, il che indica che il 93,11% della variabilità in altezza può essere spiegato dalla variabile predittrice del peso:

Questo ci dice che il peso è un ottimo indicatore dell’altezza.

Ipotesi di regressione lineare

Affinché i risultati di un modello di regressione lineare siano validi e affidabili, dobbiamo verificare che siano soddisfatte le seguenti quattro ipotesi:

1. Relazione lineare: esiste una relazione lineare tra la variabile indipendente, x, e la variabile dipendente, y.

2. Indipendenza: i residui sono indipendenti. In particolare, non esiste alcuna correlazione tra i residui consecutivi nei dati delle serie temporali.

3. Omoschedasticità: i residui hanno una varianza costante ad ogni livello di x.

4. Normalità: i residui del modello sono distribuiti normalmente.

Se uno o più di questi presupposti non vengono soddisfatti, i risultati della nostra regressione lineare potrebbero essere inaffidabili o addirittura fuorvianti.

Fare riferimento a questo articolo per una spiegazione di ciascun presupposto, come determinare se il presupposto è soddisfatto e cosa fare se il presupposto non è soddisfatto.