Come eseguire anova unidirezionale in excel

Un’ANOVA unidirezionale (“analisi della varianza”) viene utilizzata per determinare se esiste o meno una differenza statisticamente significativa tra le medie di tre o più gruppi indipendenti.

Questo tutorial spiega come eseguire un’ANOVA unidirezionale in Excel.

Esempio: ANOVA unidirezionale in Excel

Supponiamo che un ricercatore recluti 30 studenti per partecipare a uno studio. Gli studenti vengono assegnati in modo casuale a utilizzare una delle tre tecniche di studio nelle tre settimane successive per prepararsi a un esame. Alla fine delle tre settimane, tutti gli studenti sostengono lo stesso test.

I risultati dei test degli studenti sono mostrati di seguito:

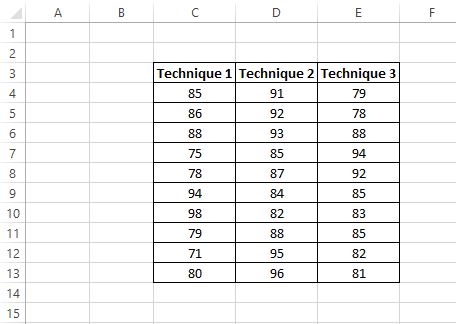
Il ricercatore vuole eseguire un’ANOVA unidirezionale per determinare se i punteggi medi sono gli stessi nei tre gruppi.

Per eseguire ANOVA unidirezionale in Excel, vai alla scheda Dati , quindi fai clic sull’opzione Analisi dati nel gruppo Analisi .

Se non vedi l’opzione Analisi dati , devi prima caricare il software gratuito Analysis ToolPak .

Dopo aver fatto clic su di esso, verrà visualizzata una finestra con diverse opzioni dello strumento di scansione. Selezionare Anova: Fattore singolo , quindi fare clic su OK .

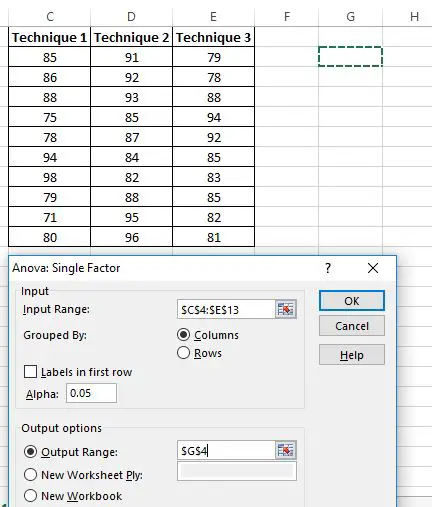
Viene visualizzata una nuova finestra che richiede un intervallo di input . Puoi trascinare una casella attorno ai tuoi dati o inserire manualmente l’intervallo di dati. In questo caso, i nostri dati sono nelle celle C4:E13 .

Successivamente, scegli un livello Alpha per il test. Per impostazione predefinita, questo numero è 0,05. In questo caso, lo lascerò a 0,05.

Infine, scegli una cella per l’ Intervallo di output , dove verranno visualizzati i risultati ANOVA unidirezionali. In questo caso, scelgo la cella G4 .

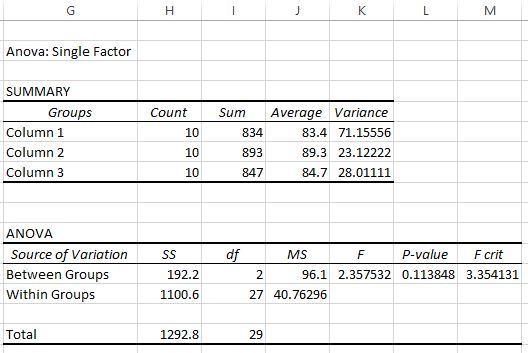
Dopo aver fatto clic su OK , verrà visualizzato il risultato ANOVA unidirezionale:

Interpretazione del risultato

Nell’output vengono visualizzate due tabelle. La prima è una tabella riepilogativa che mostra il numero di punteggi dei test in ciascun gruppo, la somma dei punteggi dei test, la media dei punteggi dei test e la varianza dei punteggi dei test.

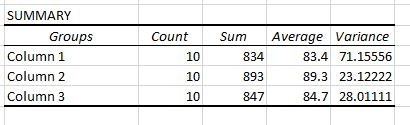
Ricordiamo che un’ANOVA unidirezionale viene utilizzata per determinare se esiste o meno una differenza statisticamente significativa tra le medie di tre o più gruppi.

Da questa prima tabella possiamo vedere che il punteggio medio per ciascuno dei tre gruppi è diverso, ma per sapere se queste differenze sono statisticamente significative dobbiamo guardare la seconda tabella.

La seconda tabella mostra la statistica del test F, il valore F critico e il valore p:

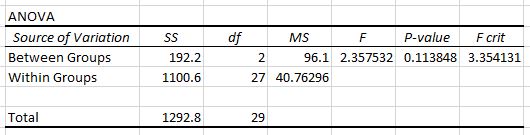
In questo caso, la statistica del test F è 2.3575 e il valore critico di F è 3.3541 . Poiché la statistica del test F è inferiore al valore critico di F, non abbiamo prove sufficienti per rifiutare l’ipotesi nulla che le medie dei tre gruppi siano uguali.

Ciò significa che non abbiamo prove sufficienti per affermare che esiste una differenza nei risultati dei test tra le tre tecniche di studio.

Potremmo anche usare il valore p per raggiungere la stessa conclusione. In questo caso, il valore p è 0,1138 , che è superiore al livello alfa di 0,05 .

Ciò significa che non abbiamo prove sufficienti per rifiutare l’ipotesi nulla che le medie dei tre gruppi siano uguali.

Nota: nei casi in cui si rifiuta l’ipotesi nulla, è possibile eseguire un test post hoc di Tukey-Kramer per determinare esattamente quali medie di gruppo sono diverse.