Tau di kendall: definizione + esempio

In statistica, la correlazione si riferisce alla forza e alla direzione di una relazione tra due variabili. Il valore di un coefficiente di correlazione può variare da -1 a 1, dove -1 indica una relazione negativa perfetta, 0 indica nessuna relazione e 1 indica una relazione positiva perfetta.

Il coefficiente di correlazione più comunemente utilizzato è il coefficiente di correlazione di Pearson , che misura l’associazione lineare tra due variabili numeriche.

Un coefficiente di correlazione meno comunemente utilizzato è il Tau di Kendall , che misura la relazione tra due colonne di dati classificati.

La formula per calcolare il Tau di Kendall, spesso abbreviato τ, è la seguente:

τ = (CD) / (C+D)

Oro:

C = il numero di coppie corrispondenti

D = il numero di coppie discordanti

L’esempio seguente illustra come utilizzare questa formula per calcolare il coefficiente di correlazione del rango Tau di Kendall per due colonne di dati classificati.

Esempio di calcolo del Tau di Kendall

Si presuppone che due allenatori di basket classifichino 12 dei loro giocatori dal peggiore al migliore. Nella tabella seguente sono riportate le classifiche assegnate da ciascun allenatore ai giocatori:

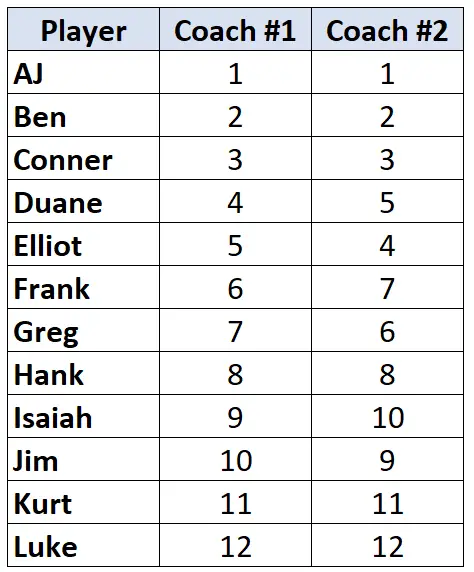
Poiché stiamo lavorando con due colonne di dati di classifica, è opportuno utilizzare il Tau di Kendall per calcolare la correlazione tra le classifiche dei due allenatori. Seguire i seguenti passaggi per calcolare il Tau di Kendall:

Passaggio 1: conta il numero di coppie corrispondenti.

Guarda solo la classifica dell’allenatore n.2. Iniziando dal primo giocatore, conta quanti ranghi sotto di lui sono più alti . Ad esempio, ci sono 11 numeri sotto “1” che sono più grandi, quindi scriveremo 11:

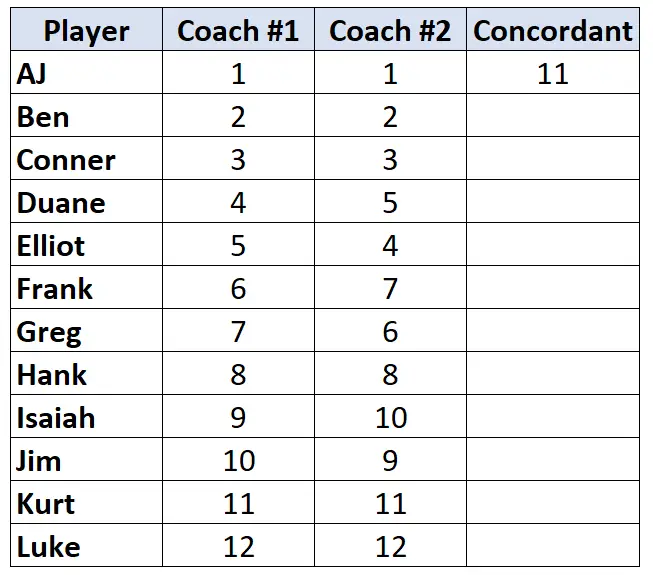
Passa al giocatore successivo e ripeti il processo. Ci sono 10 numeri sotto “2” che sono più grandi, quindi scriveremo 10:

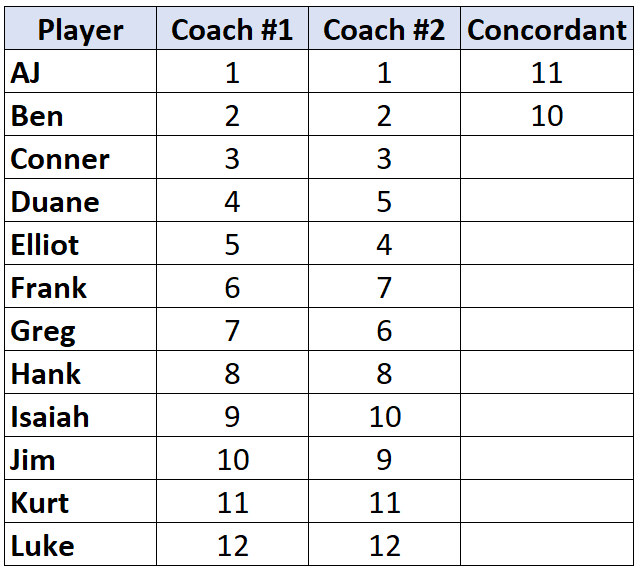
Una volta raggiunto un giocatore il cui rango è inferiore a quello del giocatore prima di lui, gli viene semplicemente assegnato lo stesso valore del giocatore prima di lui. Ad esempio, Elliot ha un grado di “4” che è inferiore al grado di “5” del giocatore precedente, quindi gli viene semplicemente assegnato lo stesso valore del giocatore prima di lui:

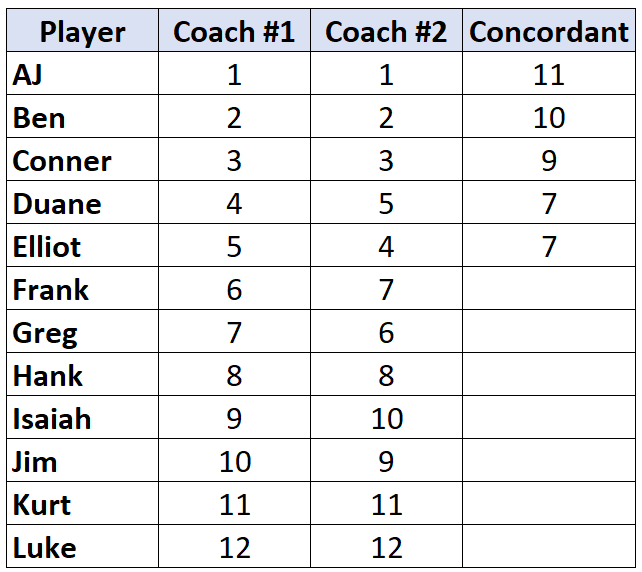
Ripeti questo processo per tutti i giocatori:

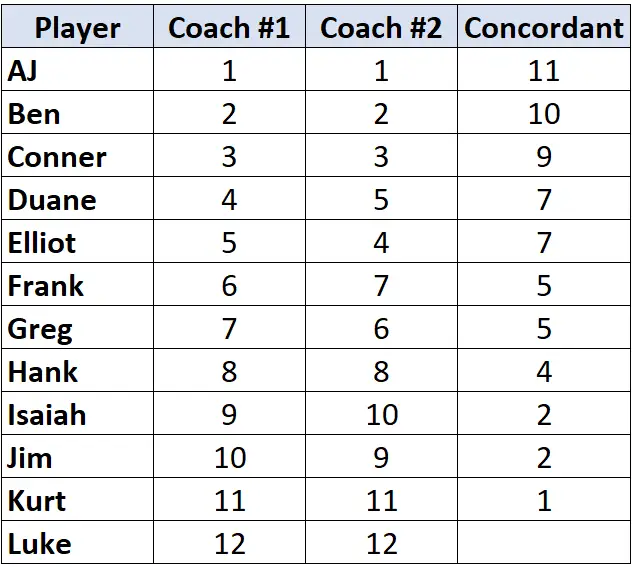
Passaggio 2: contare il numero di coppie discordanti.

Ancora una volta, guarda solo la classifica dell’allenatore n. 2. Per ogni giocatore, conta quanti ranghi sotto di lui sono più piccoli . Ad esempio, l’allenatore n. 2 ha assegnato ad AJ il grado “1” e nessun giocatore sotto di lui ha un grado inferiore. Pertanto, gli assegniamo il valore 0:

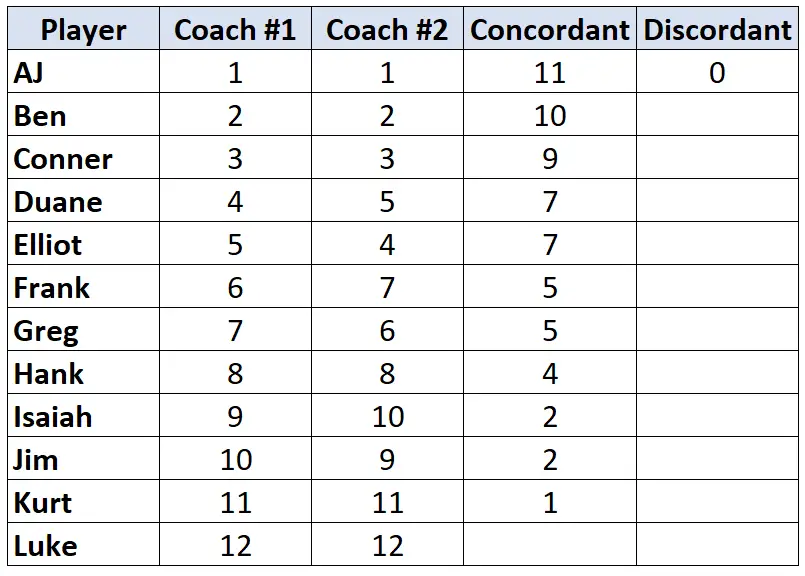
Ripeti questo procedimento per ogni giocatore:

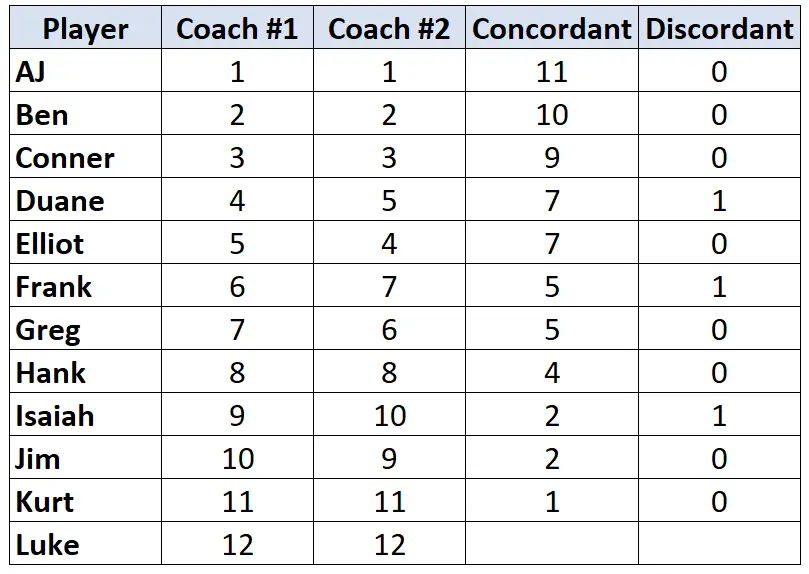
Passaggio 3: calcola la somma di ciascuna colonna e trova il Tau di Kendall.

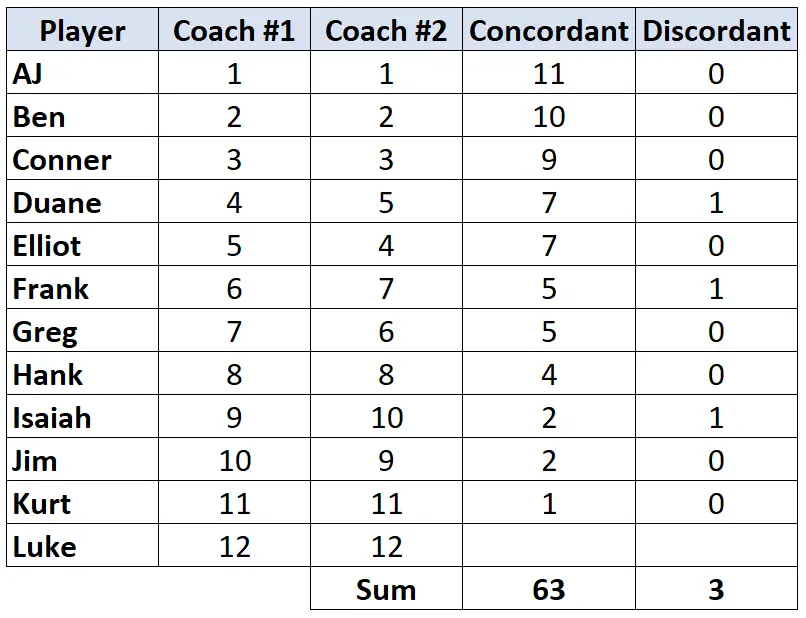
Tau di Kendall = (CD) / (C+D) = (63-3) / (63+3) = (60/66) = 0,909 .

Importanza statistica del Tau di Kendall

Quando hai più di n = 10 coppie, il Tau di Kendall segue generalmente una distribuzione normale. Puoi utilizzare la seguente formula per calcolare un punteggio z per il Tau di Kendall:

z = 3τ*√ n(n-1) / √ 2(2n+5)

Oro:

τ = valore calcolato per il Tau di Kendall

n = numero di coppie

Ecco come calcolare z per l’esempio precedente:

z = 3(.909)*√ 12(12-1) / √ 2(2*12+5) = 4.11 .

Utilizzando il calcolatore del punteggio Z del valore P, vediamo che il valore p per questo punteggio z è 0,00004 , che è statisticamente significativo al livello alfa di 0,05. Esiste quindi una correlazione statisticamente significativa tra i gradi assegnati ai giocatori dai due allenatori.

Bonus: come calcolare il Tau di Kendall in R

Nel software statistico R, è possibile utilizzare la funzione kendall.tau() della libreria VGAM per calcolare il Tau di Kendall per due vettori, che utilizza la seguente sintassi:

kendall.tau(x, y)

dove xey sono due vettori digitali di uguale lunghezza.

Il codice seguente illustra come calcolare il Tau di Kendall per i dati esatti utilizzati nell’esempio precedente:

 #load VGAM
library(VGAM)

#create vector for each coach's rankings
coach_1 <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12)
coach_2 <- c(1, 2, 3, 5, 4, 7, 6, 8, 10, 9, 11, 12)

#calculate Kendall's Tau
kendall.tau(coach_1, coach_2)

#[1] 0.9090909

Nota come il valore Tau di Kendall corrisponde al valore che abbiamo calcolato manualmente.