Come eseguire l'anova unidirezionale in stata

Un’ANOVA unidirezionale viene utilizzata per determinare se esiste o meno una differenza statisticamente significativa tra le medie di tre o più gruppi indipendenti.

Questo tipo di test è chiamato ANOVA unidirezionale perché analizziamo l’impatto di una variabile predittrice su una variabile di risposta. Se fossimo invece interessati all’impatto di due variabili predittive su una variabile di risposta, potremmo eseguire un’ANOVA a due vie .

Questo tutorial spiega come eseguire un’ANOVA unidirezionale in Stata.

Esempio: ANOVA unidirezionale in Stata

In questo esempio, utilizzeremo il set di dati Stata integrato chiamato sistolico per eseguire un’ANOVA unidirezionale. Questo set di dati contiene le seguenti tre variabili per 58 individui diversi:

• Droga utilizzata
• Malattia del paziente
• Variazione della pressione arteriosa sistolica

Utilizzeremo i seguenti passaggi per eseguire un’ANOVA unidirezionale per determinare se il tipo di farmaco utilizzato ha un impatto significativo sulla variazione della pressione arteriosa sistolica.

Passaggio 1: caricare i dati.

Innanzitutto, carica i dati digitando webuse systolic nella casella di comando e facendo clic su Invio.

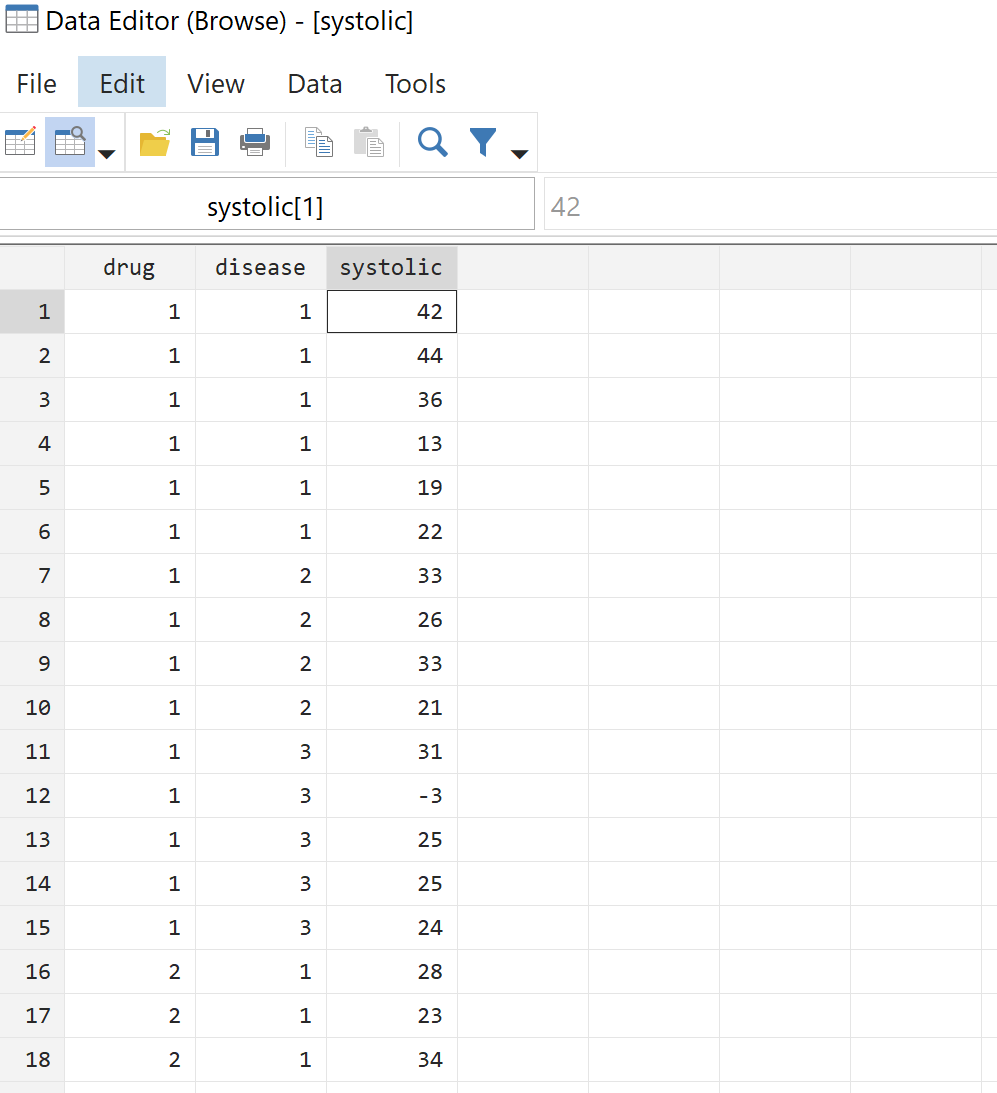
Passaggio 2: visualizzare i dati grezzi.

Prima di eseguire un’ANOVA unidirezionale, diamo prima un’occhiata ai dati grezzi. Dalla barra dei menu in alto, vai a Dati > Editor di dati > Editor di dati (Sfoglia) . Questo ci mostrerà i dati effettivi per tutti i 58 pazienti:

Passaggio 3: visualizzare i dati.

Successivamente, visualizziamo i dati. Creeremo box plot per visualizzare la distribuzione dei valori di pressione arteriosa sistolica per ciascuna categoria di farmaci.

Dalla barra dei menu in alto, vai su Grafici > Box plot . In variabili, scegli Sistolica:

Quindi, nella sottovoce Categorie sotto Variabile di raggruppamento, scegli farmaco:

Fare clic su OK . Verrà visualizzato automaticamente un grafico con quattro boxplot:

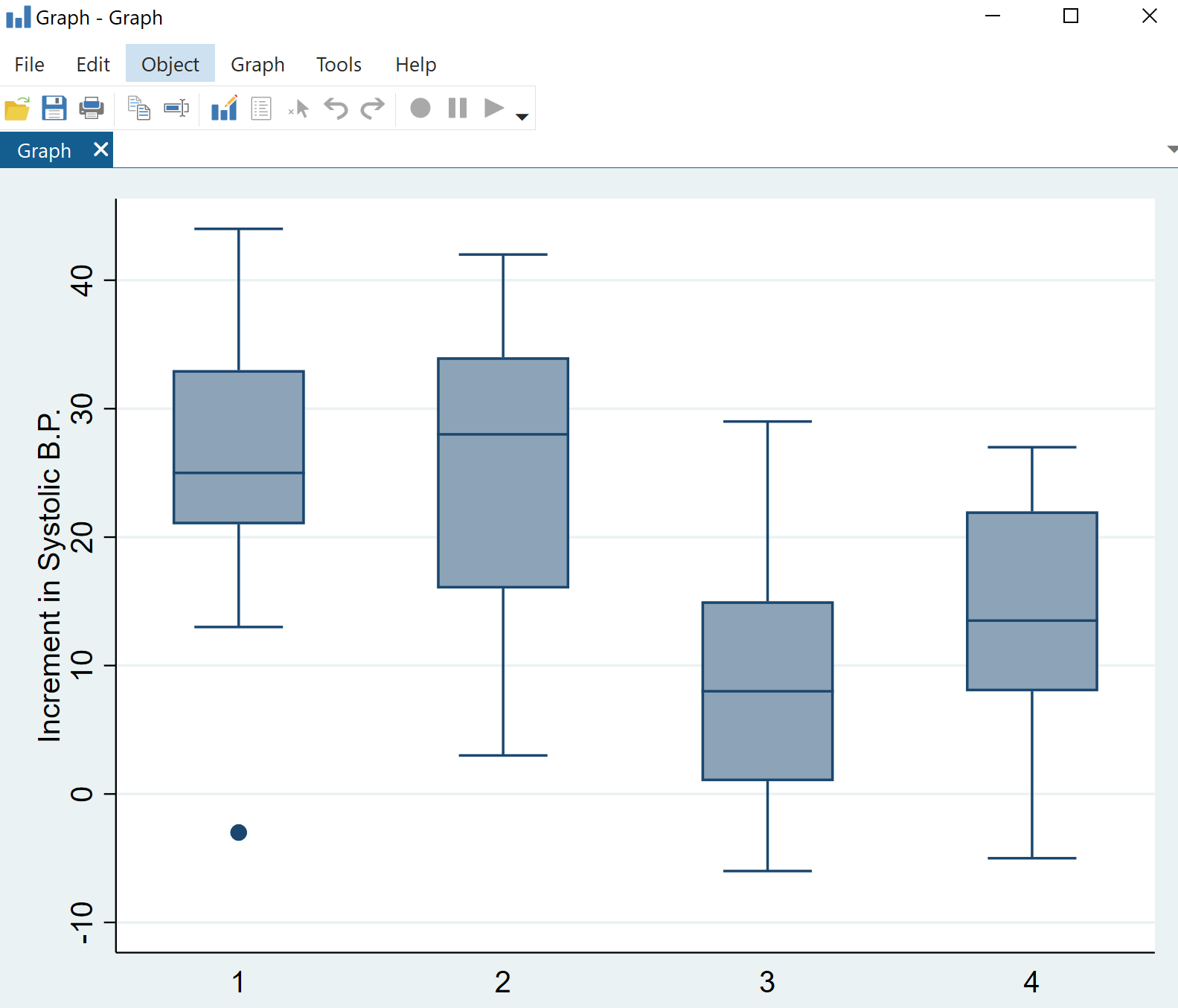
Possiamo immediatamente vedere che la distribuzione delle variazioni della pressione arteriosa sistolica varia tra le categorie di farmaci, ma un’ANOVA unidirezionale ci dirà se queste differenze sono statisticamente significative.

Passaggio 4: eseguire un’ANOVA unidirezionale.

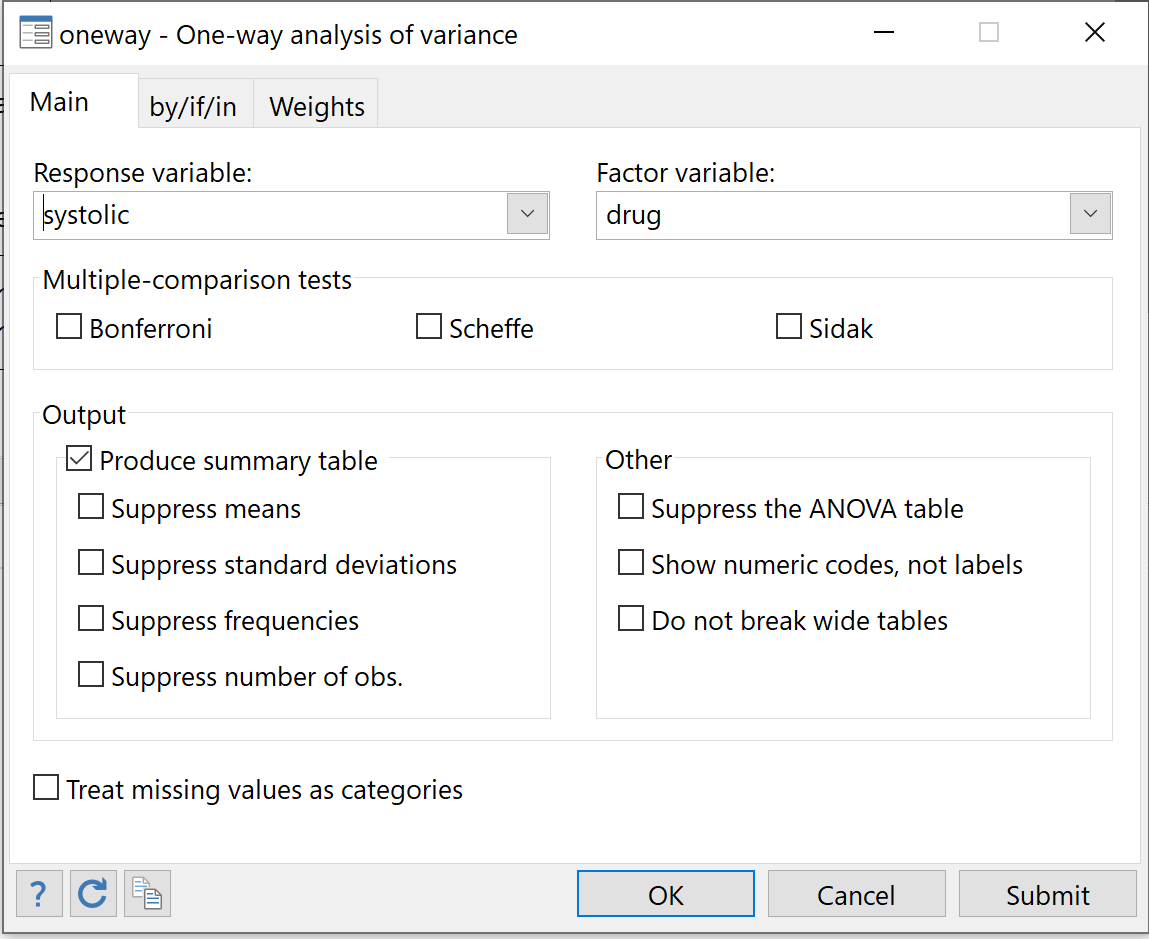
Dalla barra dei menu in alto, vai a Statistiche > Modelli lineari e correlati > ANOVA/MANOVA > ANOVA unidirezionale .

In Variabile di risposta, scegli Sistolica. Sotto il fattore variabile, scegli il farmaco. Quindi fare clic sulla casella accanto a Tabella riepilogativa dei prodotti in modo da poter visualizzare alcune statistiche descrittive di base per ciascun gruppo. Quindi fare clic su OK .

Verrà visualizzato il seguente output:

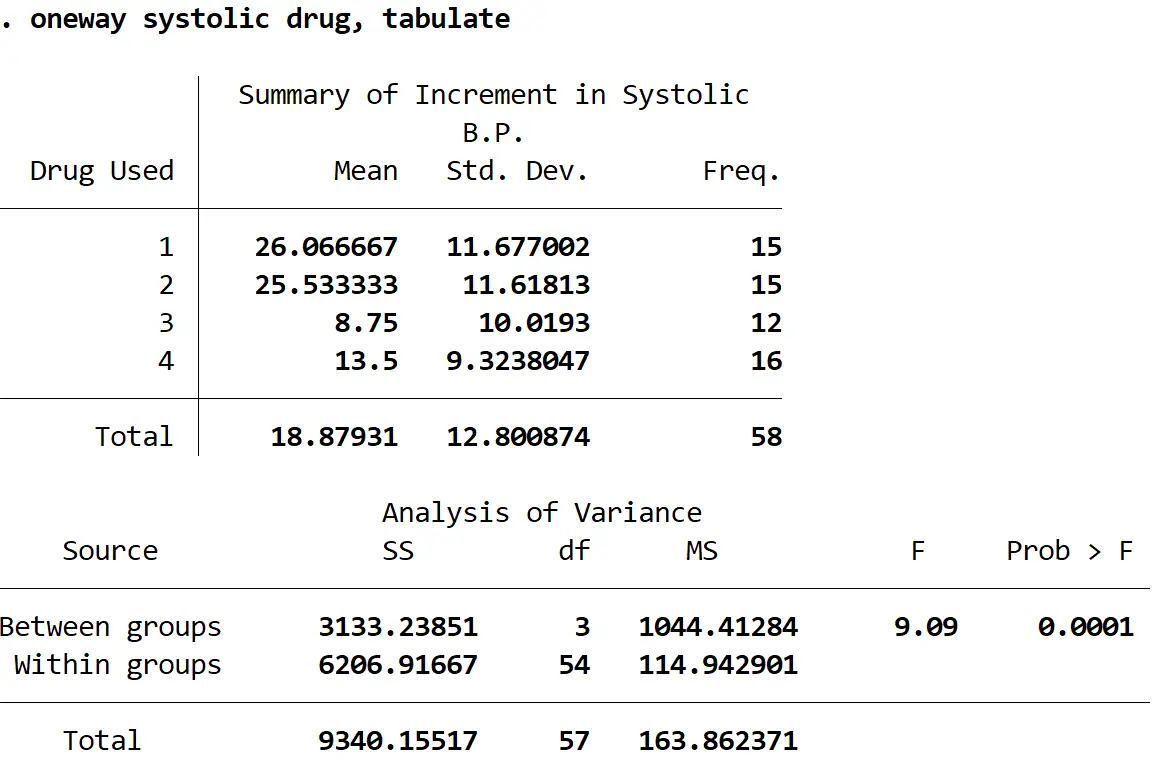
La statistica F è 9,09 e il valore p corrispondente è 0,0001 . Poiché il valore p è inferiore a alfa = 0,05, possiamo rifiutare l’ipotesi nulla secondo cui la variazione media della pressione arteriosa sistolica per ciascun gruppo è uguale.

In altre parole, esiste una differenza statisticamente significativa nella variazione media della pressione arteriosa sistolica tra almeno due gruppi di farmaci.

Passaggio 5: esegui più test comparativi.

Quindi possiamo eseguire diversi test comparativi per scoprire effettivamente quali medie di gruppo sono diverse l’una dall’altra.

Dalla barra dei menu in alto, vai a Statistiche > Riepiloghi, tabelle e test > Statistiche riassuntive e descrittive > Confronti a coppie di medie .

Per Variabile, scegliere la variabile Risposta sistolica . Per Over scegliere la variabile esplicativa farmaco . Per Regolazione per confronti multipli, scegliere il metodo Tukey .

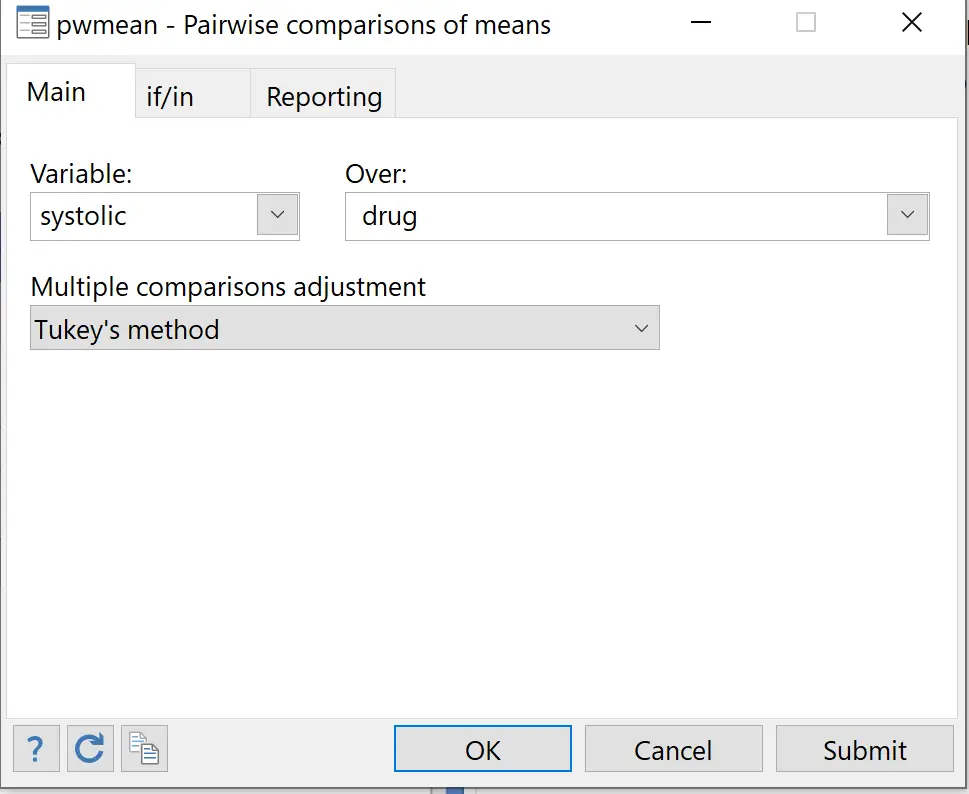
Quindi, nella sottovoce Reporting , fai clic sul pulsante accanto a Tabelle degli effetti e seleziona la casella accanto a Mostra tabella degli effetti con intervalli di confidenza e valori p . Quindi fare clic su OK .

Verranno visualizzati i seguenti risultati:

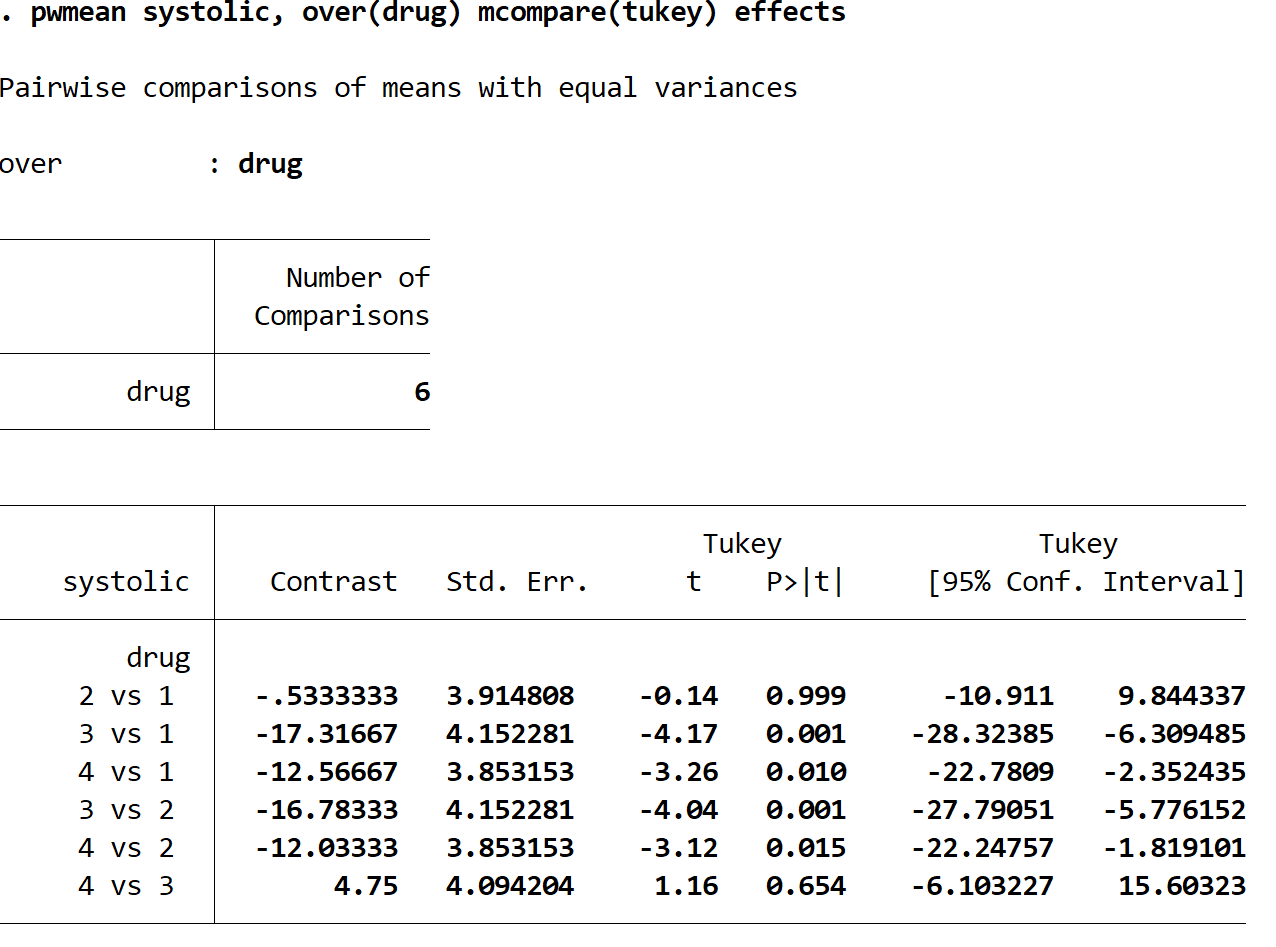
Ogni riga rappresenta un confronto tra due gruppi di farmaci specifici. Ad esempio, la prima riga confronta la variazione media della pressione sanguigna sistolica tra il gruppo di farmaci 2 e il gruppo di farmaci 1. Il valore p per questo confronto è 0,999 , che è estremamente alto e non inferiore a 0,05. Ciò significa che non esiste alcuna differenza statisticamente significativa tra i gruppi di farmaci 1 e 2.

Tuttavia, possiamo vedere che i valori p per i seguenti confronti sono tutti inferiori a 0,05:

• medicina 3 a 1 | valore p = 0,001
• medicina 4 a 1 | valore p = 0,010
• medicina 3 contro 2 | valore p = 0,001
• medicina 4 contro 2 | valore p = 0,015

Ciò significa che la differenza nella variazione media della pressione arteriosa sistolica è statisticamente significativa tra ciascuno di questi gruppi.

Passaggio 6: riportare i risultati.

Infine, riporteremo i risultati della nostra analisi ANOVA unidirezionale. Ecco un esempio di come eseguire questa operazione:

È stata eseguita un’ANOVA unidirezionale per determinare se quattro diversi tipi di farmaci avessero effetti diversi sulla pressione arteriosa sistolica.

La tabella seguente riassume il numero di partecipanti in ciascun gruppo, nonché la variazione media della pressione arteriosa sistolica e la deviazione standard della pressione arteriosa sistolica per ciascun gruppo:

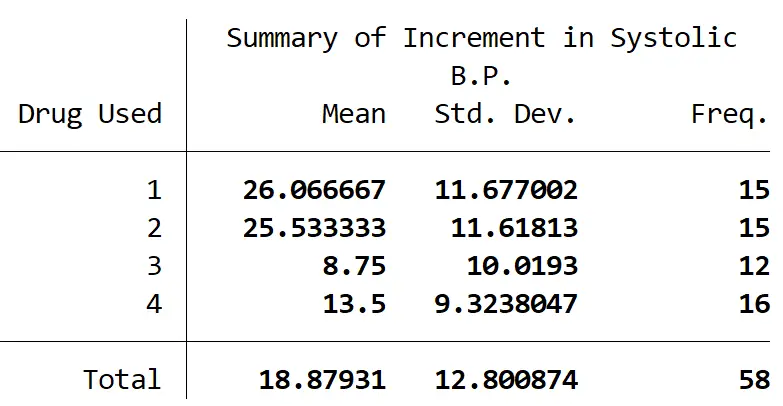
Un’ANOVA unidirezionale ha rivelato che c’era una differenza statisticamente significativa tra almeno due gruppi (F(3, 54) = 9,09, p = 0,001).

Il test di Tukey per confronti multipli ha rivelato che la variazione della pressione arteriosa sistolica era più elevata in modo statisticamente significativo per il farmaco 3 rispetto al farmaco 1 (17,32 +/- 4,15, p = 0,001), per il farmaco 3 rispetto al farmaco 2 (16,78 +/- 4,15, p = 0,001), per il farmaco 4 rispetto al farmaco 1 (12,57 +/- 3,85, p = 0,010) e per il farmaco 4 rispetto al farmaco 2 (12,03 +/- 3,85, p = 0,015).

Non è stata riscontrata alcuna differenza statisticamente significativa tra i gruppi di farmaci 1 e 2 (0,533 +/- 3,91, p = 0,999) o tra i gruppi di farmaci 3 e 4 (4,75 +/- 4,09, p = 0,654).