Come eseguire un test kruskal-wallis a stata

Un test di Kruskal-Wallis viene utilizzato per determinare se esiste o meno una differenza statisticamente significativa tra le mediane di tre o più gruppi indipendenti. È considerato l’equivalente non parametrico dell’ANOVA unidirezionale .

Questo tutorial spiega come eseguire un test Kruskal-Wallis in Stata.

Come eseguire un test Kruskal-Wallis a Stata

Per questo esempio utilizzeremo il set di dati Census , che contiene i dati del censimento del 1980 per tutti i cinquanta stati degli Stati Uniti. Nel set di dati, gli stati sono classificati in quattro diverse regioni:

• Nord Est
• Centro-Nord
• Sud
• ovest

Effettueremo un test Kruskal-Wallis per determinare se l’età media è uguale in queste quattro regioni.

Passaggio 1: caricare e visualizzare i dati.

Innanzitutto, carica il set di dati digitando il seguente comando nella casella Comando:

utilizzare https://www.stata-press.com/data/r13/census

Ottieni un breve riepilogo del set di dati utilizzando il seguente comando:

riassumere

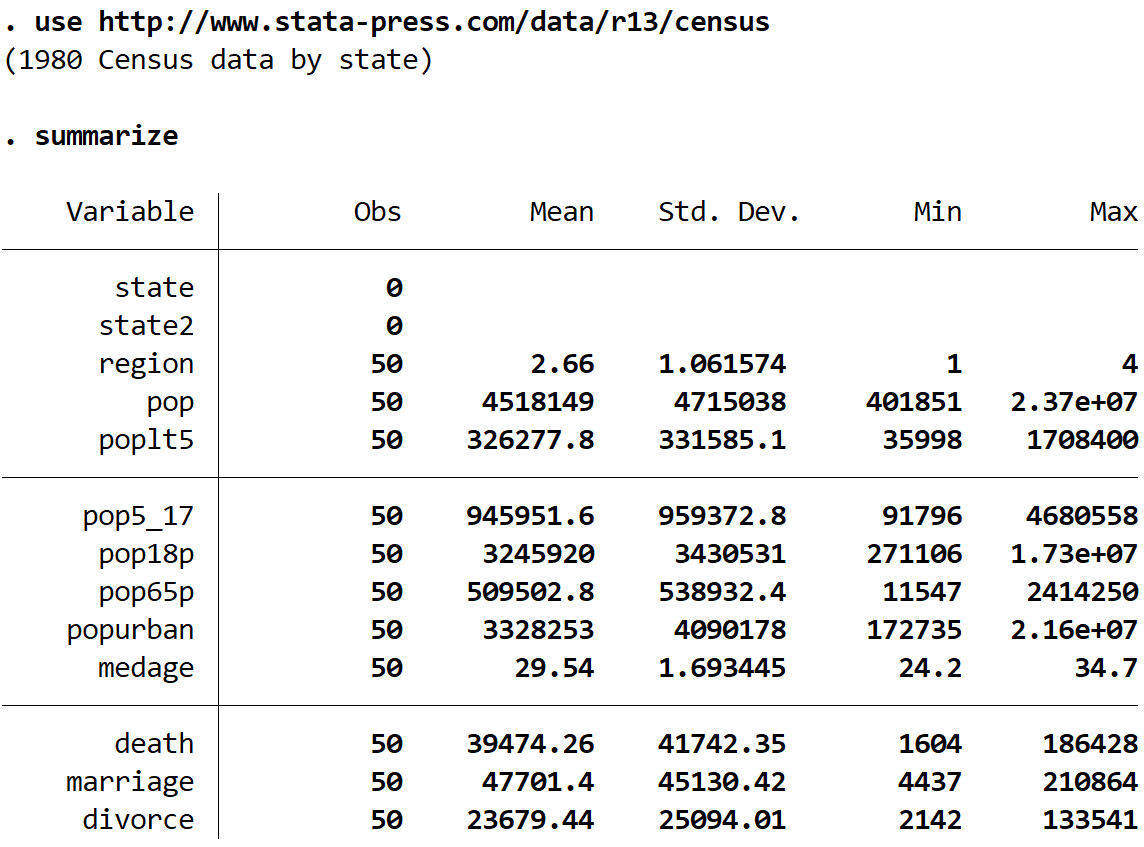
Possiamo vedere che ci sono 13 variabili diverse in questo set di dati, ma le uniche due con cui lavoreremo sono medage (età mediana) e regione .

Passaggio 2: visualizzare i dati.

Prima di eseguire il test di Kruskal-Wallis, creiamo alcuni box plot per visualizzare la distribuzione mediana dell’età per ciascuna delle quattro regioni:

casella grafica Medage, su (regione)

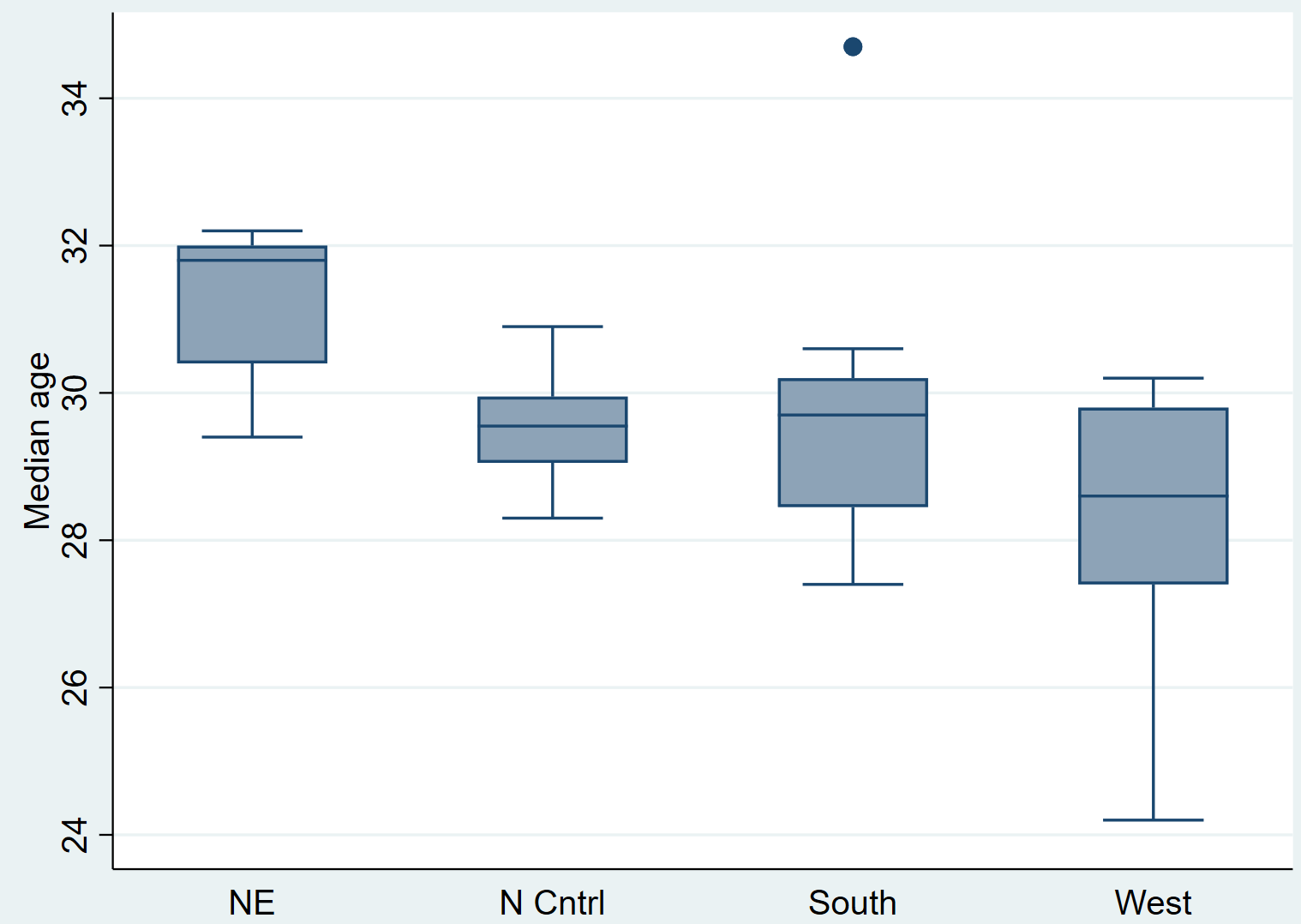
Basta osservare i box plot per notare che le distribuzioni sembrano variare da regione a regione. Eseguiremo quindi un test di Kruskal-Wallis per vedere se queste differenze sono statisticamente significative.

Passaggio 3: eseguire un test Kruskal-Wallis.

Utilizzare la seguente sintassi per eseguire un test Kruskal-Wallis:

kwallis misura_variabile, per (raggruppamento_variabile)

Nel nostro caso utilizzeremo la seguente sintassi:

kwallis medage, di (regione)

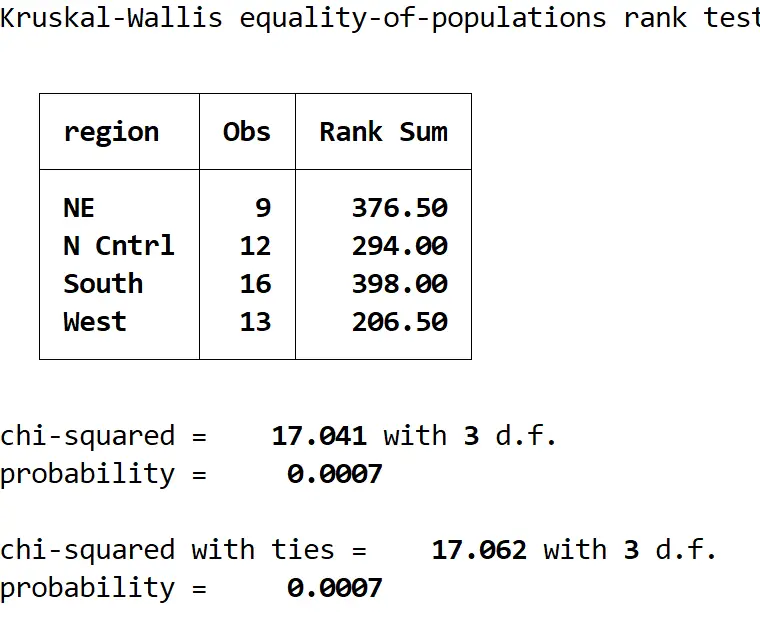
Ecco come interpretare il risultato:

Tabella riepilogativa: questa tabella mostra il numero di osservazioni per regione e le somme della classifica per ciascuna regione.

Chi quadrato con parità: questo è il valore della statistica del test, che risulta essere 17.062.

probabilità: questo è il valore p che corrisponde alla statistica del test, che risulta essere 0,0007. Poiché questo valore è inferiore a 0,05, possiamo rifiutare l’ipotesi nulla e concludere che l’età mediana non è uguale nelle quattro regioni.

Passaggio 4: riportare i risultati.

Riportiamo infine i risultati del test di Kruskal-Wallis. Ecco un esempio di come eseguire questa operazione:

È stato eseguito un test Kruskal-Wallist per determinare se l’età media degli individui era la stessa nelle seguenti quattro regioni degli Stati Uniti:

• Nord-est (n=9)
• Centro-Nord (n=12)
• Sud (n=16)
• Ovest (n=13)

Il test ha rivelato che l’età media degli individui non era la stessa (X ² = 17,062, p = 0,0007) nelle quattro regioni. Cioè, c’era una differenza statisticamente significativa nell’età media tra due o più regioni.