Varianza

Di Agosto 5, 2023 Statistiche 0 commenti

In questo articolo spieghiamo cos’è la varianza, chiamata anche varianza, e come viene calcolata. Troverai la formula della varianza, un esempio concreto di calcolo della varianza e, inoltre, potrai calcolare la varianza di qualsiasi set di dati con un calcolatore online.

Ti mostriamo anche come trovare la varianza dei dati raggruppati, poiché ciò viene fatto in modo diverso. Infine, ti insegniamo la differenza tra varianza della popolazione e varianza del campione, la differenza tra varianza e deviazione standard e le proprietà di questa misura statistica.

Cos’è la varianza?

In statistica, la varianza è una misura di dispersione che indica la variabilità di una variabile casuale. La varianza è uguale alla somma dei quadrati dei residui divisa per il numero totale di osservazioni.

Tieni presente che il residuo è inteso come la differenza tra il valore di un punto dati statistico e la media del set di dati.

Nella teoria della probabilità, il simbolo della varianza è la lettera greca sigma al quadrato (σ 2 ). Sebbene sia solitamente rappresentato anche come Var(X) , dove X è la variabile casuale da cui viene calcolata la varianza.

In generale, interpretare il valore della varianza di una variabile casuale è semplice. Maggiore è il valore della varianza, maggiore è la dispersione dei dati. E viceversa, minore è il valore della varianza, minore sarà la dispersione nella serie di dati. Tuttavia, quando si interpreta la varianza, bisogna fare attenzione ai valori anomali , poiché possono distorcere il valore della varianza.

varianza, altre misure considerate oltre alla dispersione sono l’intervallo, la deviazione standard, la deviazione media e il coefficiente di variazione.

Come calcolare il divario

Per calcolare la varianza è necessario eseguire i seguenti passaggi:

  1. Trova la media aritmetica del set di dati.
  2. Calcolare i residui, definiti come la differenza tra i valori e la media del set di dati.
  3. Quadra ogni resto.
  4. Aggiungi tutti i risultati calcolati nel passaggio precedente.
  5. Dividere per il numero totale di dati. Il risultato ottenuto è la varianza della serie di dati.

In conclusione, la formula per calcolare la varianza di un set di dati è:

varianza

Oro:

  • X

    è la variabile casuale di cui si vuole calcolare la varianza.

  • x_i

    è il valore dei dati

    i

    .

  • n

    è il numero totale di osservazioni.

  • \overline{X}

    è la media della variabile casuale

    X

    .

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare la varianza di qualsiasi set di dati.

Pertanto, per estrarre la varianza da una serie di dati, è essenziale sapere come viene calcolata la media aritmetica. Se non ricordi come farlo, puoi verificarlo nell’articolo collegato sopra.

Esempio di deviazione

Ora che conosciamo la definizione di varianza, risolveremo passo dopo passo un esercizio in modo che tu possa vedere come si ottiene la varianza di una serie di dati.

  • Di una multinazionale è noto il risultato economico che ha avuto negli ultimi cinque anni, nella maggior parte ha ottenuto utili ma un anno ha presentato perdite considerevoli: 11,5,2, -9,7 milioni di euro. Calcola la varianza di questo set di dati.

Come abbiamo visto nella spiegazione precedente, la prima cosa che dobbiamo fare per trovare la varianza di una serie di dati è calcolarne la media aritmetica:

\overline{X}=\cfrac{11+5+2+(-9)+7}{5}=3,2

E una volta che conosciamo il valore medio dei dati, possiamo utilizzare la formula della varianza:

Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}

Sostituiamo i dati forniti dalla dichiarazione di esercizio nella formula:

Var(X)=\cfrac{\displaystyle (11-3,2)^2+(5-3,2)^2+(2-3,2)^2+(-9-3,2)^2+(7-3,2)^2}{5}

Infine non resta che risolvere le operazioni per calcolare la varianza:

\begin{aligned}Var(X)&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5}\\[2ex]&= \cfrac{228,8}{5} \\[2ex]&=45,76 \ \text{millones de euros}^2\end{aligned}

Si noti che le unità di varianza sono le stesse unità dei dati statistici ma al quadrato, per questo motivo la varianza di questo gruppo di dati è pari a 45,76 milioni di euro 2 .

Calcolatore del divario

Inserisci un set di dati statistici nella seguente calcolatrice per calcolarne la varianza. I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.

Varianza per dati raggruppati

Per calcolare la varianza dei dati raggruppati in intervalli è necessario seguire i seguenti passaggi:

  1. Trova la media dei dati raggruppati.
  2. Calcolare i residui dei dati raggruppati.
  3. Quadra ogni resto.
  4. Moltiplicare ciascun risultato precedente per la frequenza del suo intervallo.
  5. Aggiungi la somma di tutti i valori ottenuti nel passaggio precedente.
  6. Dividere per il numero totale di osservazioni. Il numero risultante è la varianza dei dati raggruppati.

In altre parole, la formula per calcolare la varianza dei dati raggruppati in intervalli è la seguente:

Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}

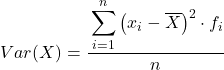
Sebbene venga normalmente utilizzata la formula sopra, è possibile utilizzare anche l’espressione algebrica seguente poiché è equivalente:

Var(X)=\cfrac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{n}-\overline{X}^2

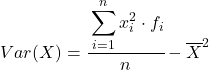
Ad esempio, troveremo la varianza delle seguenti serie di dati raggruppati:

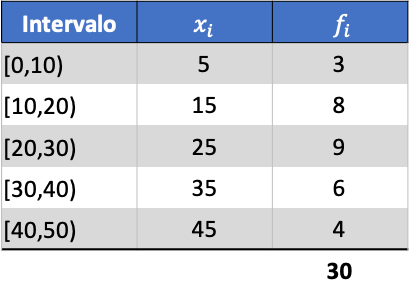
dati raggruppati in intervalli

Innanzitutto, dobbiamo determinare la media dei dati raggruppati. Per fare ciò, aggiungiamo una colonna nella tabella delle frequenze con il prodotto del voto della classe e della frequenza:

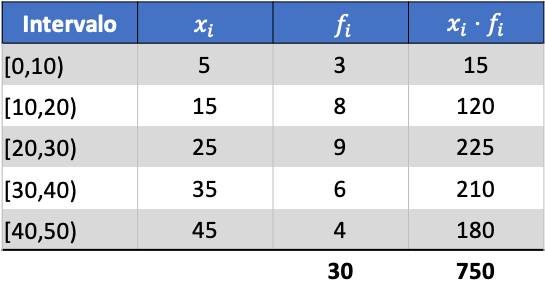
dati raggruppati con la media

Calcoliamo ora la media dei dati raggruppati dividendo la somma della colonna aggiunta per il numero totale di dati:

\overline{X}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{n}=\cfrac{750}{30}=25

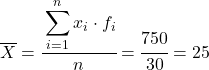
E dalla media dei dati calcolati, possiamo aggiungere le seguenti tre colonne:

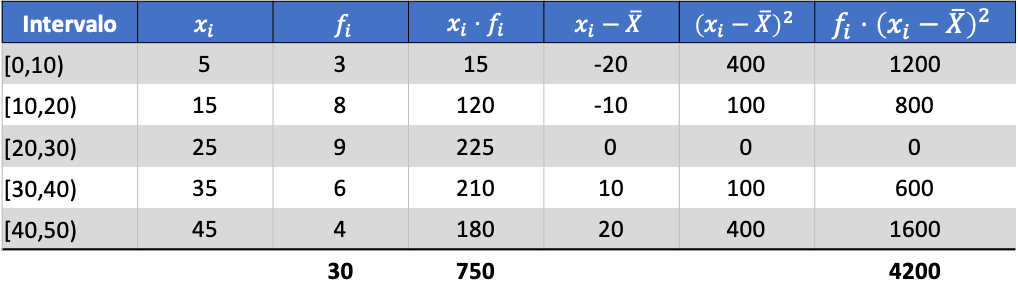
varianza per dati raggruppati

Quindi la varianza del set di dati raggruppati è la somma dell’ultima colonna divisa per il numero totale di dati osservati:

Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}=\cfrac{4200}{30}=140

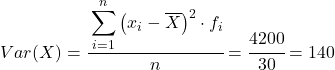
Varianza e deviazione standard

Varianza e deviazione standard (o deviazione standard) sono due misure di dispersione e quindi indicano entrambe il grado di dispersione dell’insieme di dati. Tuttavia, la differenza tra varianza e deviazione standard è che in generale la varianza ha valori maggiori, poiché è il quadrato della deviazione standard.

La deviazione standard è generalmente rappresentata dalla lettera greca sigma (σ), e per questo motivo la varianza è rappresentata dalla lettera sigma al quadrato (σ 2 ), poiché è la relazione matematica che esiste tra queste due metriche di dispersione.

Var(X)=\sigma^2

Quindi, una volta calcolato il valore della varianza di un insieme di dati, puoi facilmente trovare il valore della deviazione standard di quello stesso insieme semplicemente prendendo la radice quadrata della varianza.

\sigma=\sqrt{\sigma^2}

Varianza della popolazione e varianza del campione

Logicamente, la varianza della popolazione si riferisce al calcolo della varianza di una popolazione statistica e, invece, la varianza campionaria si applica al calcolo della varianza di un campione. Tuttavia, si tratta di due concetti diversi poiché la formula della varianza della popolazione è diversa dalla formula della varianza campionaria.

Normalmente negli esercizi sulla varianza, se non ci dicono diversamente, per trovare la varianza del set di dati fornito dobbiamo utilizzare la formula della varianza della popolazione , che è quella che abbiamo spiegato all’inizio dell’articolo:

\sigma^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}

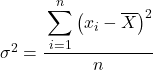
Ma forse in alcuni problemi ti viene chiesto di trattare i dati statistici come un campione, nel qual caso dobbiamo utilizzare la formula della varianza campionaria :

s^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n-1}

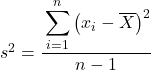
Si noti che per indicare che si sta calcolando la varianza della popolazione, questa è indicata dalla lettera greca σ, ma quando si sta calcolando la varianza campionaria, viene utilizzata la lettera s.

Come puoi vedere, l’unica differenza tra le due formule è che nella varianza di un campione dobbiamo dividere per il numero totale di osservazioni meno 1, ad esempio, se ci sono 30 dati in totale, divideremo per 29 Ma il calcolo del numeratore si fa esattamente nello stesso modo.

Proprietà della varianza

La varianza ha le seguenti proprietà:

  • La varianza di qualsiasi variabile casuale sarà sempre maggiore o uguale a zero. Allo stesso modo, se la varianza è zero, significa che tutti i dati statistici sono uguali.

Var(x)\ge 0

  • Ovviamente, la varianza di un singolo valore è zero.

Var(a)=0\qquad a\in \mathbb{R}

  • La varianza del prodotto di uno scalare per una variabile è equivalente a quello scalare al quadrato moltiplicato per la varianza della variabile.

Var(aX)=a^2\cdot Var(X)\qquad a\in \mathbb{R}

  • La varianza della somma di due variabili dipendenti è equivalente alla somma della varianza di ciascuna variabile separatamente più il doppio della covarianza tra le due variabili.

Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)

  • Di conseguenza, se le due variabili sono indipendenti, per determinare la varianza della loro somma è sufficiente sommare le loro varianze:

Var(X+Y)=Var(X)+Var(Y)

  • La deviazione può anche essere definita con l’aspettativa matematica utilizzando la seguente formula:

Var(X)=E\bigl[(X-\overline{X})^2\bigr]

Informazioni sull'autore

Dr. Benjamin Anderson
Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più

Aggiungi un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *