Come calcolare le probabilità normali su una calcolatrice ti-84
La distribuzione normale è la distribuzione più comunemente utilizzata in tutte le statistiche. Questo tutorial spiega come utilizzare le seguenti funzioni su una calcolatrice TI-84 per trovare le probabilità della distribuzione normale:
normalpdf(x, μ, σ) restituisce la probabilità associata alla pdf normale dove:
- x = valore individuale
- μ = media della popolazione
- σ = deviazione standard della popolazione
normalcdf(lower_x, upper_x, μ, σ) restituisce la probabilità cumulativa associata al normal cdf tra due valori.
Oro:
- lower_x = valore individuale inferiore
- upper_x = valore individuale superiore
- μ = media della popolazione
- σ = deviazione standard della popolazione
Queste due funzioni sono accessibili su una calcolatrice TI-84 premendo 2nd quindi premendo vars . Questo ti porterà a una schermata DISTR in cui potrai quindi utilizzare normalpdf() e normalcdf() :
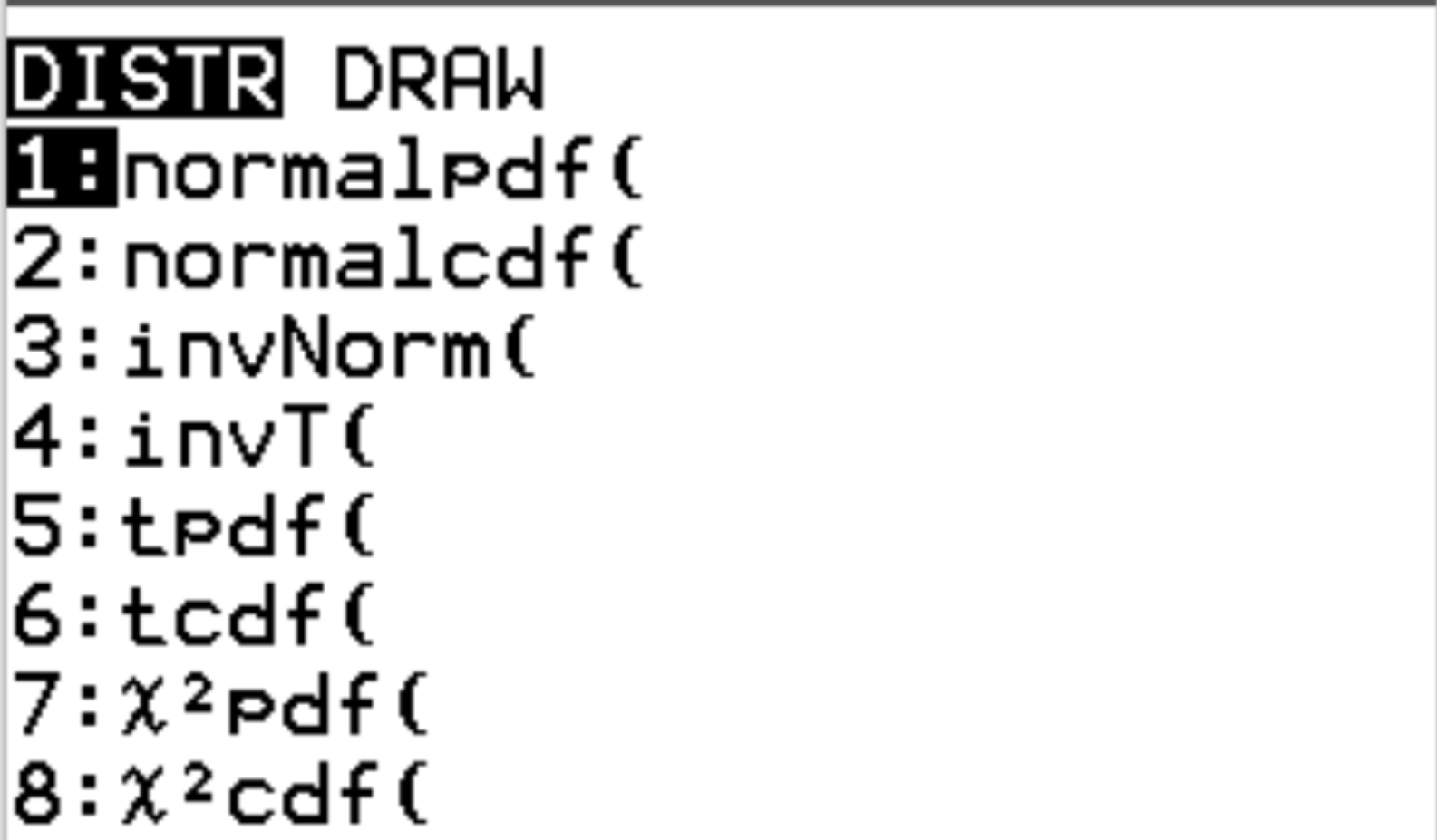
Gli esempi seguenti illustrano come utilizzare queste funzioni per rispondere a domande diverse.
Esempio 1: probabilità normale maggiore di x
Domanda: Per una distribuzione normale con media = 40 e deviazione standard = 6, trova la probabilità che un valore sia maggiore di 45.
Risposta: utilizzare la funzione normalcdf(x, 10000, μ, σ):
cdfnormale(45, 10000, 40, 6) = 0,2023
Nota: poiché la funzione richiede un valore upper_x, utilizziamo semplicemente 10.000.
Esempio 2: probabilità normale inferiore a x
Domanda: Per una distribuzione normale con media = 100 e deviazione standard = 11,3, trova la probabilità che un valore sia inferiore a 98.
Risposta: utilizzare la funzione normalcdf(-10000, x, μ, σ):
normalcdf(-10000, 98, 100, 11,3) = 0,4298
Nota: poiché la funzione richiede un valore lower_x, utilizziamo semplicemente -10000.
Esempio 3: Probabilità normale tra due valori
Domanda: Per una distribuzione normale con media = 50 e deviazione standard = 4, trova la probabilità che un valore sia compreso tra 48 e 52.
Risposta: utilizzare la funzione normalcdf(smaller_x, Larger_x, μ, σ).
cdfnormale(48, 52, 50, 4) = 0,3829
Esempio 4: Probabilità normale a parte due valori
Domanda: Per una distribuzione normale con media = 22 e deviazione standard = 4, trova la probabilità che un valore sia inferiore a 20 o maggiore di 24.
Risposta: utilizzare la funzione normalcdf(-10000, small_x, μ, σ) + normalcdf(larger_x, 10000, μ, σ)
cdfnormale(-10000, 20, 22, 4) + cdfnormale(24, 10000, 22, 4) = 0,6171