Un'introduzione alla distribuzione binomiale

La distribuzione binomiale è una delle distribuzioni più popolari in statistica. Per comprendere la distribuzione binomiale, è utile innanzitutto comprendere gli esperimenti binomiali .

Esperimenti binomiali

Un esperimento binomiale è un esperimento che ha le seguenti proprietà:

• L’esperimento consiste in n prove ripetute.
• Ogni prova ha solo due possibili esiti.
• La probabilità di successo, indicata con p , è la stessa per ogni prova.
• Ogni test è indipendente.

L’esempio più ovvio di esperimento binomiale è il lancio di una moneta. Ad esempio, supponiamo di lanciare una moneta 10 volte. Questo è un esperimento binomiale perché ha le seguenti quattro proprietà:

• L’esperimento consiste in n prove ripetute – Ci sono 10 prove.
• Ogni prova ha solo due possibili esiti: testa o croce.
• La probabilità di successo, indicata con p , è la stessa per ogni prova. Se definiamo “successo” l’atterraggio delle teste, allora la probabilità di successo è esattamente 0,5 per ogni prova.
• Ogni prova è indipendente – Il risultato di un lancio di moneta non influenza il risultato di qualsiasi altro lancio di moneta.

La distribuzione binomiale

La distribuzione binomiale descrive la probabilità di ottenere k successi in n esperimenti binomiali.

Se una variabile casuale X segue una distribuzione binomiale, la probabilità che X = k successo può essere trovata con la seguente formula:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Oro:

• n: numero di prove
• k: numero di successi
• p: probabilità di successo in una determinata prova
• _n C _k : il numero di modi per ottenere k successi in n prove

Ad esempio, supponiamo di lanciare una moneta 3 volte. Possiamo usare la formula sopra per determinare la probabilità di ottenere 0, 1, 2 e 3 teste con questi 3 lanci:

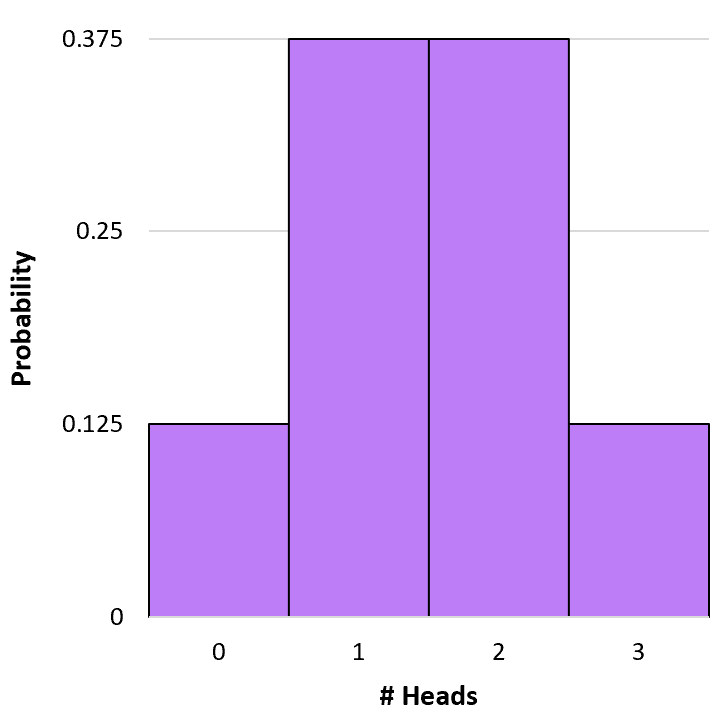
P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125

P(X=1) = ₃ C ₁ * 0,5 ¹ * (1-0,5) ^3-1 = 3 * 0,5 * (0,5) ² = 0,375

P(X=2) = ₃ C ₂ * 0,5 ² * (1-0,5) ^3-2 = 3 * 0,25 * (0,5) ¹ = 0,375

P(X=3) = ₃ C ₃ * 0,5 ³ * (1-0,5) ^3-3 = 1 * 0,125 * (0,5) ⁰ = 0,125

Nota : abbiamo utilizzato questo calcolatore combinato per calcolare _{nCk per} ciascun esempio.

Possiamo creare un semplice istogramma per visualizzare questa distribuzione di probabilità:

Calcolo delle probabilità binomiali cumulative

È semplice calcolare una singola probabilità binomiale (ad esempio la probabilità che una moneta esca testa 1 volta su 3 lanci) utilizzando la formula sopra, ma per calcolare le probabilità binomiali cumulative dobbiamo aggiungere le probabilità individuali.

Ad esempio, supponiamo di voler conoscere la probabilità che una moneta esca testa 1 volta o meno su 3 lanci. Utilizzeremmo la seguente formula per calcolare questa probabilità:

P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .

Questa è chiamata probabilità cumulativa perché implica l’aggiunta di più probabilità. Possiamo calcolare la probabilità cumulativa di ottenere k teste o meno per ciascun risultato utilizzando una formula simile:

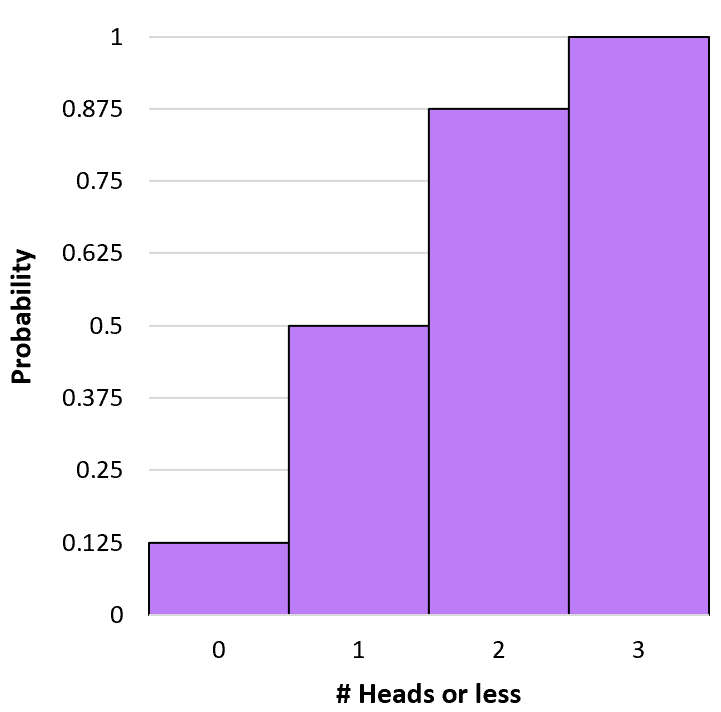
P(X≤0) = P(X=0) = 0,125 .

P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .

P(X≤2) = P(X=0) + P(X=1) + P(X=2) = 0,125 + 0,375 + 0,375 = 0,875 .

P(X≤3) = P(X=0) + P(X=1) + P(X=2) + P(X=3) = 0,125 + 0,375 + 0,375 + 0,125 = 1 .

Possiamo creare un istogramma per visualizzare questa distribuzione di probabilità cumulativa:

Calcolatore della probabilità binomiale

Quando lavoriamo con numeri piccoli (ad esempio 3 lanci di una moneta), è ragionevole calcolare manualmente le probabilità binomiali. Tuttavia, quando lavoriamo con numeri più grandi (ad esempio 100 estrazioni), può essere difficile calcolare manualmente le probabilità. In questi casi può essere utile utilizzare un calcolatore di probabilità binomiale come quello seguente.

Ad esempio, supponiamo di lanciare una moneta n = 100 volte, la probabilità che esca testa in una data prova è p = 0,5 e vogliamo conoscere la probabilità che esca testa k = 43 volte o meno:

Ecco come interpretare il risultato:

• La probabilità che esca testa esattamente 43 volte è 0,03007 .
• La probabilità che la moneta esca testa meno di 43 volte è 0,06661 .
• La probabilità che la moneta esca testa 43 volte o meno è 0,09667 .
• La probabilità che la moneta esca testa più di 43 volte è 0,90333 .
• La probabilità che la moneta esca testa 43 volte o più è 0,93339 .

Proprietà della distribuzione binomiale

La distribuzione binomiale ha le seguenti proprietà:

La media della distribuzione è μ = np

La varianza della distribuzione è σ ² = np(1-p)

La deviazione standard della distribuzione è σ = √ np(1-p)

Ad esempio, supponiamo di lanciare una moneta 3 volte. Sia p = la probabilità che esca testa.

Il numero medio di teste che ci aspettiamo è μ = np = 3*.5 = 1.5 .

La varianza del numero dei presenti che ci aspettiamo è σ ² = np(1-p) = 3*.5*(1-.5) = 0.75 .

Problemi pratici di distribuzione binomiale

Utilizza i seguenti problemi pratici per verificare la tua conoscenza della distribuzione binomiale.

Problema 1

Domanda: Bob effettua il 60% dei suoi tiri liberi. Se effettua 12 tiri liberi, qual è la probabilità che ne effettui esattamente 10?

Risposta: utilizzando il calcolatore della distribuzione binomiale sopra con p = 0,6, n = 12 e k = 10, troviamo che P(X=10) = 0,06385 .

Problema 2

Domanda: Jessica lancia una moneta 5 volte. Qual è la probabilità che esca testa 2 volte o meno?

Risposta: utilizzando il calcolatore della distribuzione binomiale sopra con p = 0,5, n = 5 e k = 2, troviamo che P(X≤2) = 0,5 .

Problema 3

Domanda: La probabilità che un dato studente venga accettato in una determinata università è 0,2. Se si candidano 10 studenti, qual è la probabilità che ne vengano accettati più di 4?

Risposta: utilizzando il calcolatore della distribuzione binomiale sopra con p = 0,2, n = 10 e k = 4, troviamo che P(X>4) = 0,03279 .

Problema 4

Domanda: lanci una moneta 12 volte. Qual è il numero medio previsto di teste che appariranno?

Risposta: ricorda che la media di una distribuzione binomiale è calcolata come μ = np. Quindi, μ = 12*0,5 = 6 teste .

Problema 5

Domanda: Mark fa un fuoricampo nel 10% dei suoi tentativi. Se effettua 5 tentativi in una determinata partita, qual è la varianza nel numero di fuoricampo che effettua?

Risposta: Ricordiamo che la varianza di una distribuzione binomiale è calcolata come σ ² = np(1-p). Pertanto, ^σ2 = 6*.1*(1-.1) = 0,54 .

Risorse addizionali

I seguenti articoli possono aiutarti a imparare come utilizzare la distribuzione binomiale in diversi software statistici:

• Come calcolare le probabilità binomiali in Excel
• Come calcolare le probabilità binomiali su una calcolatrice TI-84
• Come calcolare le probabilità binomiali in R
• Come tracciare una distribuzione binomiale in R