Differenza media

Di Benjamin anderson Agosto 5, 2023 Statistiche 0 commenti

Questo articolo spiega cos’è la deviazione media e come viene calcolata. Troverai anche esempi concreti di calcolo della deviazione media. Inoltre, potrai calcolare la deviazione media di qualsiasi set di dati statistici utilizzando un calcolatore online.

Cos’è la deviazione media?

La deviazione media , chiamata anche deviazione media assoluta , è una misura della dispersione statistica.

La deviazione media di un set di dati è la media delle deviazioni assolute . Pertanto, la deviazione media è uguale alla somma delle deviazioni di ciascun dato dalla media aritmetica divisa per il numero totale di dati.

In altre parole, la formula per la deviazione media è la seguente:

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare la deviazione media di qualsiasi set di dati.

In statistica, la deviazione media è chiamata anche deviazione media assoluta .

L’interpretazione dello scostamento medio avviene nel seguente modo: maggiore è il valore dello scostamento medio, significa che i dati sono, in media, più lontani dalla media aritmetica; al contrario, minore è la deviazione media, più vicino è il valore. i dati sono. La deviazione media indica quindi la dispersione di una serie di dati.

Altre misure considerate distribuite sono l’intervallo, l’intervallo interquartile, la deviazione standard (o deviazione standard), la varianza e il coefficiente di variazione.

Come calcolare la deviazione media

Per calcolare la deviazione media di una serie di dati, è necessario seguire i seguenti passaggi:

Calcolare la media aritmetica del set di dati statistici.
Calcolare la deviazione di ciascun punto dati dalla media, definita come il valore assoluto della differenza tra i dati e la media.
Somma tutte le differenze calcolate nel passaggio precedente.
Dividere per il numero totale di dati. Il risultato ottenuto è la deviazione media della serie di dati.

In sintesi, la formula da applicare per trovare lo scostamento medio è:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

Esempio di calcolo della deviazione media

Considerando la definizione di deviazione media, di seguito è riportato un esempio risolto passo passo del calcolo della deviazione media di un campione statistico. In questo modo capirai meglio come ottenere la deviazione media.

Un analista studia i risultati economici di un’azienda nell’ultimo anno e dispone di informazioni sull’utile ottenuto dall’azienda durante ogni trimestre di quell’anno: 2, 3, 7 e 5 milioni di dollari. Qual è la deviazione media dei dati?

Innanzitutto, dobbiamo calcolare la media dei dati, quindi sommiamo e dividiamo per il numero totale di osservazioni (4):

$\overline{x}=\cfrac{2+3+7+5}{4}=4,25$

Una volta calcolata la media aritmetica, utilizziamo la formula della deviazione media:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

Sostituiamo i dati nella formula:

$D_{\overline{x}}=\cfrac{|2-4,25|+|3-4,25|+|7-4,25|+|5-4,25|}{4}$

Facciamo i calcoli al numeratore:

$D_{\overline{x}}=\cfrac{|-2,25|+|-1,25|+|2,75|+|0,75|}{4}$

$D_{\overline{x}}=\cfrac{2,25+1,25+2,75+0,75}{4}$

$D_{\overline{x}}=\cfrac{7}{4}$

Infine, dividiamo per il numero totale di dati per ottenere la deviazione media del campione:

$D_{\overline{x}}=1,75$

Calcolatore della deviazione media

Inserisci una serie di dati statistici nella seguente calcolatrice per calcolare la sua deviazione media. I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.

Deviazione media per i dati raggruppati

Per calcolare la deviazione media dei dati raggruppati in intervalli, è necessario seguire i seguenti passaggi:

Determinare la media aritmetica del set di dati statistici. Poiché i dati sono raggruppati, l’espressione per calcolare la media è:

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}$

Calcolare la deviazione di ciascun intervallo dalla media, che equivale al valore assoluto della differenza tra il voto della classe e la media.

$|x_i-\overline{x}|$

Moltiplicare la deviazione di ciascun intervallo per la sua frequenza assoluta.

$|x_i-\overline{x}|\cdot f_i$

Somma tutti i risultati del passaggio precedente, quindi dividi per il numero totale di dati. Il risultato ottenuto è la deviazione media del campione raggruppato in intervalli.

$\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

In conclusione, la formula per ottenere la deviazione media dai dati raggruppati è:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

Quando i dati sono raggruppati, di solito significa che ce ne sono molti e che trovare la deviazione media richiede molti passaggi. Pertanto, per eseguire il calcolo vengono solitamente utilizzate tabelle di frequenza.

Di seguito è riportato un esercizio passo passo su come calcolare la deviazione media quando i dati sono raggruppati in intervalli:

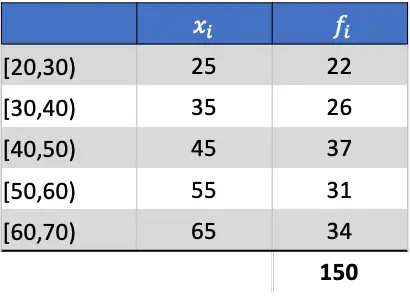
La prima cosa da fare è calcolare la media dei dati raggruppati. Per fare ciò, aggiungiamo una colonna alla tabella moltiplicando la nota della classe per la sua frequenza:

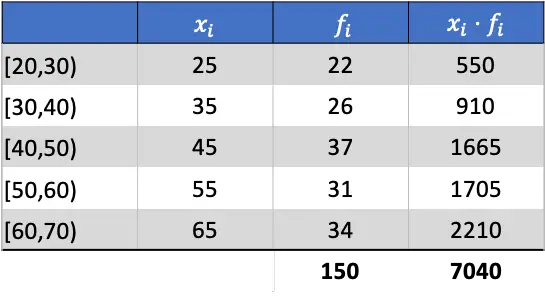
La media aritmetica sarà quindi il risultato della divisione della somma della colonna aggiunta per la somma delle frequenze assolute:

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}=\cfrac{7040}{150}=46,93$

Ora che conosciamo la media dei dati, possiamo aggiungere tutte le colonne necessarie per trovare la deviazione media:

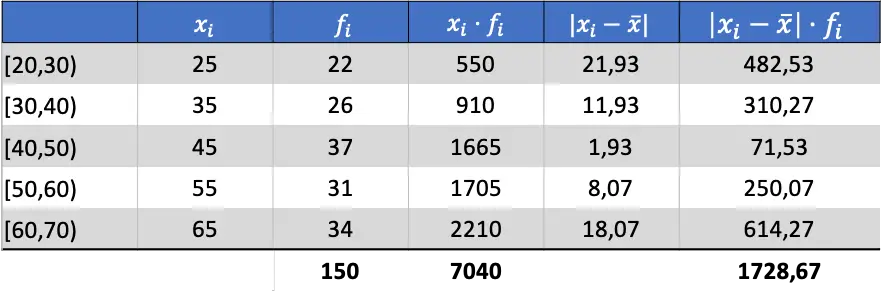
Pertanto, per ottenere la deviazione media è necessario dividere la somma dell’ultima colonna per il numero totale di osservazioni:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}=\cfrac{1728,67}{150}=11,52$

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più