Covarianza

Di Benjamin anderson Agosto 5, 2023 Statistiche 0 commenti

Questo articolo spiega cos’è la covarianza e come viene calcolata. Troverai la formula di covarianza e un esempio di calcolo della covarianza di un set di dati. Inoltre, puoi calcolare la covarianza di qualsiasi serie di dati con il calcolatore online alla fine.

Cos’è la covarianza?

In statistica, la covarianza è un valore che indica il grado di variazione congiunta di due variabili casuali. In altre parole, la covarianza viene utilizzata per analizzare la dipendenza tra due variabili.

La covarianza è uguale alla somma dei prodotti delle differenze tra i dati delle due variabili e le rispettive medie divisa per il numero totale di dati.

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare la covarianza di qualsiasi set di dati.

L’interpretazione del valore di covarianza è molto semplice:

Se la covarianza è positiva significa che esiste una dipendenza tra le due variabili. Pertanto, quando una variabile aumenta di valore, aumenta anche l’altra variabile, e viceversa.
Se la covarianza è negativa , significa che la relazione tra le due variabili è negativa. Quindi, quando una variabile aumenta di valore, l’altra variabile diminuisce e viceversa.
Se la covarianza è zero (o il suo valore è vicino allo zero), ciò implica che non esiste alcuna relazione tra le due variabili. In altre parole, le due variabili casuali sono indipendenti.

Come calcolare la covarianza

Per calcolare la covarianza di una serie di dati, è necessario eseguire i seguenti passaggi:

Calcolare la media di ciascuna variabile separatamente.
Per ogni variabile, trova la differenza tra ciascuno dei suoi valori e la media della variabile.
Moltiplicare le differenze calcolate nel passaggio precedente per ciascun punto dati.
Somma tutti i risultati ottenuti nel passaggio precedente.
Dividere per il numero totale di dati. Il valore ottenuto è la covarianza della serie di dati.

In sintesi, la formula per calcolare la covarianza tra due variabili è la seguente:

$Cov(X,Y)=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}$

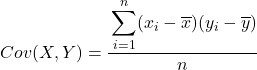
Un metodo altamente consigliato per estrarre la covarianza tra due variabili è creare una tabella con tutte le coppie di dati e aggiungere una colonna per ciascuno dei passaggi spiegati sopra. In questo modo i tuoi calcoli saranno organizzati molto meglio e capirai meglio cosa stai facendo.

Esempio di calcolo della covarianza

Considerando la definizione di covarianza, di seguito è riportato un esempio passo passo del calcolo di questo tipo di misura statistica. L’obiettivo è comprendere meglio il concetto di covarianza e come analizzare la correlazione tra due variabili.

Calcolare la covarianza del seguente set di dati statistici:

Per prima cosa dobbiamo calcolare la media aritmetica di ciascuna variabile. Per fare ciò, dividiamo la somma dei valori di ciascuna variabile per il numero totale di dati.

$\overline{x}=\cfrac{58}{10}=5,8$

$\overline{y}=\cfrac{51}{10}=5,1$

➤ Vedi: media delle formule aritmetiche

Una volta determinata la media di ciascuna variabile casuale, possiamo aggiungere le seguenti colonne alla tabella dati per ottenere la covarianza:

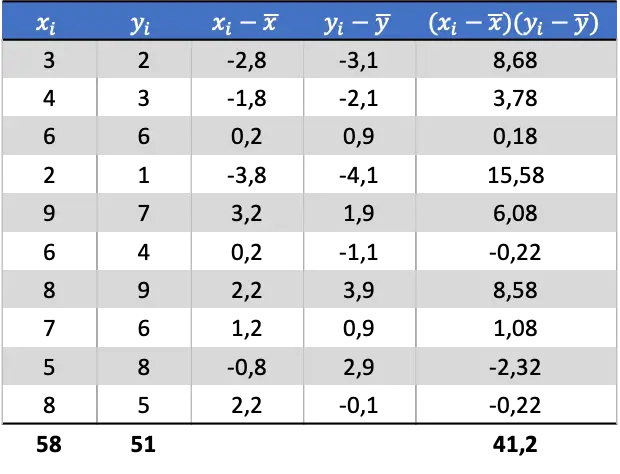
Quindi per determinare la covarianza delle due variabili devi dividere la somma dell’ultima colonna per il numero di coppie di dati:

$\begin{aligned}Cov(X,Y)&=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}\\[2ex] Cov(X,Y)&= \cfrac{41,2}{10} \\[2ex]Cov(X,Y)&= 4,12\end{aligned}$

In questo caso il valore di covarianza è positivo, il che significa che esiste una dipendenza diretta tra le due variabili casuali studiate. Tuttavia, se il valore della covarianza fosse stato negativo, ciò significherebbe che la dipendenza tra le due variabili è inversa. E infine, se il valore della covarianza è zero o molto vicino allo zero, significa che non esiste una relazione lineare tra le due variabili.

Come puoi vedere risolvendo questo esempio, è molto utile utilizzare un programma per computer come Excel per aggiungere colonne alla tabella ed eseguire rapidamente i calcoli. Altrimenti, calcolando manualmente le operazioni, occorre molto più tempo per trovare la covarianza.

Calcolatore della covarianza

Inserisci una serie di dati statistici nella seguente calcolatrice per calcolare la covarianza tra due variabili. È necessario separare le coppie di dati, in modo che nella prima casella ci siano solo i valori di una variabile e nella seconda casella ci siano solo i valori della seconda variabile.

I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.

Proprietà di covarianza

La covarianza ha le seguenti proprietà:

La covarianza tra una variabile casuale e una costante è zero.

$Cov(X,a)=0$

La covarianza di una variabile e di se stessa è equivalente alla varianza di quella variabile.

$Cov(X,X)=Var(X)$

➤ Vedi: cos’è la varianza?

La covarianza soddisfa la proprietà di simmetria, quindi la covarianza delle variabili X e Y è uguale alla covarianza delle variabili Y e X. L’ordine delle variabili non influisce sul risultato della covarianza.

$Cov(X,Y)=Cov(Y,X)$

Se le variabili vengono moltiplicate per le costanti, puoi prima calcolare la covarianza e poi moltiplicare il risultato per le costanti.

$Cov(a\cdot X,b\cdot Y)=a\cdot b\cdot Cov(X,Y)$

L’aggiunta di termini alle variabili non influisce sul risultato della covarianza.

$Cov(a+X,b+Y)=Cov(X+Y)$

La covarianza tra due variabili casuali è legata alle loro aspettative matematiche. La covarianza tra le variabili X e Y è uguale all’aspettativa matematica del prodotto di X e Y meno il prodotto dell’aspettativa matematica di ciascuna variabile.

$Cov(X,Y)=E[X\cdot Y]-E[X]\cdot E[Y]$

Quando si opera con variabili, la seguente espressione algebrica viene riempita rispetto alla covarianza:

$\begin{aligned}\displaystyle Cov(aX+bY,cW+dV)= \ & \displaystyle acCov(X,W)+adCov(X,V)+\\[2ex]& +bcCov(Y,W)+bdCov(Y,V)\end{aligned}$

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più