Moda (statistiche)

Di Benjamin anderson Agosto 5, 2023 Statistiche 0 commenti

Questo articolo spiega quale modalità è nelle statistiche. Imparerai come trovare la modalità statistica per dati raggruppati e dati non raggruppati, i diversi tipi di modalità e diversi esempi di questa misura statistica.

Cos’è la modalità nelle statistiche?

In statistica, la moda è il valore nel set di dati che ha la frequenza assoluta più alta, ovvero la moda è il valore più ripetuto in un set di dati.

Pertanto, per calcolare la moda di un set di dati statistici, è sufficiente contare il numero di volte in cui ciascun elemento di dati appare nel campione e i dati più ripetuti costituiranno la moda.

La moda viene utilizzata per definire una distribuzione statistica, poiché il valore più ripetuto è solitamente al centro della distribuzione.

Si può anche dire che la modalità è modalità statistica o valore modale . Allo stesso modo, quando i dati vengono raggruppati in intervalli, l’intervallo più ripetuto è l’ intervallo modale o la classe modale .

In generale, il termine Mo viene utilizzato come simbolo per la modalità statistica, ad esempio la modalità di distribuzione X è Mo(X).

Tieni presente che la modalità è una misura statistica della posizione centrale, nonché della mediana e della media. Di seguito vedremo cosa significa ciascuna di queste misure statistiche.

Tipi di modalità nelle statistiche

In statistica esistono diversi tipi di modalità classificate in base al numero di valori più ripetuti:

Modalità unimodale : esiste un solo valore con il numero massimo di ripetizioni. Ad esempio, [1, 4, 2, 4, 5, 3].
Modalità bimodale : il numero massimo di ripetizioni si verifica con due valori diversi ed entrambi i valori vengono ripetuti lo stesso numero di volte. Ad esempio, [2, 6, 7, 2, 3, 6, 9].
Modalità multimodale : tre o più valori hanno lo stesso numero massimo di ripetizioni. Ad esempio, [3, 3, 4, 1, 3, 4, 2, 1, 4, 5, 2, 1].

Come trovare la modalità statistica

Per trovare la modalità statistica di un set di dati, è necessario seguire i seguenti passaggi:

Metti in ordine i dati. Questo passaggio non è obbligatorio, ma renderà più semplice il conteggio dei numeri.
Conta quante volte appare ciascun numero.
Il numero che appare più spesso è la modalità statistica.

Esempi di modalità statistica

Considerando la definizione di moda nelle statistiche, di seguito puoi vedere un esempio di ogni tipologia di moda in modo da poter comprendere meglio il concetto.

Esempio di modalità unimodale

Qual è la modalità del seguente set di dati?

$5 \ 4 \ 9 \ 7 \ 2 \ 3 \ 9 \ 6 \ 5 \ 2 \ 5$

I numeri non sono ordinati, quindi li ordineremo prima per facilitare la ricerca della modalità.

$2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 7 \ 9 \ 9$

I numeri 2 e 9 compaiono due volte, ma il numero 5 si ripete tre volte. Pertanto, la moda della serie di dati è la numero 5.

$Mo=5$

Esempio di modalità bimodale

Calcolare la moda del seguente set di dati:

$8 \ 7 \ 0 \ 6 \ 10 \ 9 \ 13 \ 8 \ 0 \ 6 \ 2 \ 6 \ 5 \ 11 \ 10$

$0 \ 9 \ 8 \ 6 \ 12 \ 3 \ 5 \ 11 \ 1 \ 4 \ 8 \ 10 \ 2 \ 5 \ 7$

Per prima cosa mettiamo in ordine i numeri:

$0 \ 0 \ 0 \ 1 \ 2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 6 \ 6 \ 6$

$7 \ 7 \ 8 \ 8 \ 8 \ 8 \ 9 \ 9 \ 10 \ 10 \ 10 \ 11 \ 11 \ 12 \ 13$

Come puoi vedere, il numero 6 e il numero 8 compaiono quattro volte in totale, che è il numero massimo di ripetizioni. Pertanto in questo caso si tratta di una modalità bimodale e i due numeri rappresentano la modalità del dataset:

$Mo=\{ 6 \ ; \ 8\}$

Esempio di modalità multimodale

Trova la seguente modalità del set di dati:

$21 \ 27 \ 32 \ 15 \ 13 \ 20 \ 21 \ 21 \ 25 \ 27 \ 31 \ 30 \ 19 \ 20 \ 16$

$22 \ 19 \ 20 \ 31 \ 18 \ 20 \ 25 \ 26 \ 15 \ 20 \ 31 \ 31 \ 27 \ 16 \ 17$

$31 \ 27 \ 24 \ 23 \ 21 \ 27 \ 29 \ 36 \ 32 \ 30 \ 16 \ 22 \ 15 \ 14 \ 37$

Poiché i dati sono molti, li ordiniamo prima in ordine crescente per facilitare il conteggio:

$13 \ 14 \ 15\ 15\ 15 \ 16 \ 16 \ 16 \ 17 \ 18 \ 19 \ 19 \ 20 \ 20 \ 20$

$20 \ 20 \ 21 \ 21 \ 21\ 21 \ 22 \ 22 \ 23 \ 24 \ 25 \ 25 \ 26 \ 27 \ 27$

$27 \ 27 \ 27 \ 29 \ 30 \ 30 \ 31 \ 31 \ 31 \ 31 \ 31 \ 32 \ 32 \ 36 \ 37$

I numeri più ripetuti sono 20, 27 e 31, tutti e tre i numeri vengono ripetuti cinque volte. La modalità di questo esempio è quindi multimodale.

$Mo=\{ 20 \ ; \ 27 \ ; \ 31\}$

calcolatore di moda

Inserisci i dati di qualsiasi campione statistico nel seguente calcolatore online per calcolarne la modalità. I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.

Modalità per dati raggruppati

Quando abbiamo dati raggruppati sotto forma di intervalli, non sappiamo realmente quante volte ogni dato viene ripetuto, conosciamo solo la frequenza di ciascun intervallo.

Pertanto, per calcolare la modalità dei dati raggruppati in intervalli, dobbiamo utilizzare la seguente formula :

$Mo=L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i$

Oro:

L _i è il limite inferiore dell’intervallo modale (intervallo di frequenza assoluto più alto).
f _i è la frequenza assoluta dell’intervallo modale.
f _i-1 è la frequenza assoluta dell’intervallo prima del modale.
f _i+1 è la frequenza assoluta dell’intervallo dopo il modale.
A _i è la larghezza dell’intervallo modale.

Ad esempio, di seguito hai risolto un esercizio in cui viene calcolata la modalità dei dati raggruppati in intervalli:

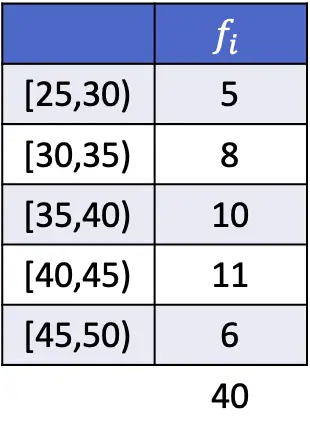
esempio di modalità statistica per dati raggruppati

In questo caso l’intervallo modale è [40,45), poiché è l’intervallo con la maggiore frequenza assoluta. Pertanto, i parametri della formula modalità per i dati raggruppati sono:

$\begin{array}{c}L_i=40\\[2ex]f_i=11\\[2ex]f_{i-1}=10\\[2ex]f_{i+1}=6\\[2ex]A_i=5\end{array}$

Applichiamo quindi la formula per determinare la modalità dei dati raggruppati in intervalli ed effettuiamo il calcolo:

$\begin{aligned}Mo & =L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i\\[2ex]& =40+ \cfrac{11-10}{(11-10)+(11-6)}\cdot 5\\[2ex]&=40,83\end{aligned}$

Differenza tra moda, media e mediana

In quest’ultima sezione vedremo qual è la differenza tra moda, media e mediana. Poiché tutte e tre sono misure statistiche della posizione centrale, il loro significato è diverso.

Come spiegato in tutto l’articolo, la moda in matematica è il valore più ripetuto in un set di dati.

In secondo luogo, la media è il valore medio di tutti i dati statistici. Pertanto, per ottenere la media di alcuni dati, è necessario sommare tutti i dati e poi dividere il risultato per il numero di osservazioni.

Infine, la mediana è il valore che occupa la posizione centrale quando i dati vengono ordinati.

Pertanto, le tre misure statistiche aiutano a definire una distribuzione di probabilità, perché forniscono un’idea dei suoi valori centrali. Ma tieni presente che non esiste una misura migliore di un’altra, significano solo concetti diversi.

Proprietà della moda

Le proprietà della moda sono:

La moda può essere trovata sia nelle variabili quantitative che nelle variabili qualitative.
Se applichiamo una trasformazione lineare ad una variabile casuale, il valore della media cambierà a seconda delle operazioni applicate.

$Mo(X)=Y \ \color{orange}\bm{\longrightarrow}\color{black} \ M(aX+b)=aY+b$

In generale, la modalità è insensibile ai valori anomali.
Se tutti i valori hanno la stessa frequenza, non esiste alcuna modalità.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più