Come calcolare l'aic in sas (con esempio)

L’Akaike Information Criterion (AIC) è una metrica utilizzata per confrontare l’adattamento di modelli di regressione multipli.

Viene calcolato come segue:

AIC = 2K – 2 ln (L)

Oro:

• K: il numero di parametri del modello. Il valore predefinito di K è 2, quindi un modello con una sola variabile predittrice avrà un valore K di 2+1 = 3.
• ln (L) : la log-verosimiglianza del modello. La maggior parte dei software statistici può calcolare automaticamente questo valore.

L’AIC è progettato per trovare il modello che spiega la maggiore variazione nei dati, penalizzando i modelli che utilizzano un numero eccessivo di parametri.

Dopo aver adattato più modelli di regressione, è possibile confrontare il valore AIC di ciascun modello. Più basso è l’AIC, più adatto è il modello.

L’esempio seguente mostra come calcolare l’AIC per diversi modelli di regressione in SAS.

Esempio: come calcolare l’AIC in SAS

Supponiamo di voler adattare tre diversi modelli di regressione lineare multipla per prevedere il voto che gli studenti otterranno in una classe all’esame.

Ecco le variabili predittive che utilizzeremo in ciascun modello:

• Variabili predittive nel modello 1: ore trascorse a studiare
• Variabili predittive nel modello 2: esami pratici passati
• Variabili predittive nel Modello 3: ore trascorse a studiare ed esami pratici sostenuti

Innanzitutto, utilizzeremo il seguente codice per creare un set di dati contenente queste informazioni per 20 studenti:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;

Successivamente, utilizzeremo proc reg per adattare ciascuno di questi modelli di regressione e utilizzeremo l’istruzione Selection=adjrsq sse aic per calcolare i valori AIC per ciascun modello:

 /*fit multiple linear regression models and calculate AIC for each model*/
proc reg data =exam_data;
    model score = hours prep_exams / selection=adjrsq sse aic;
run ; 

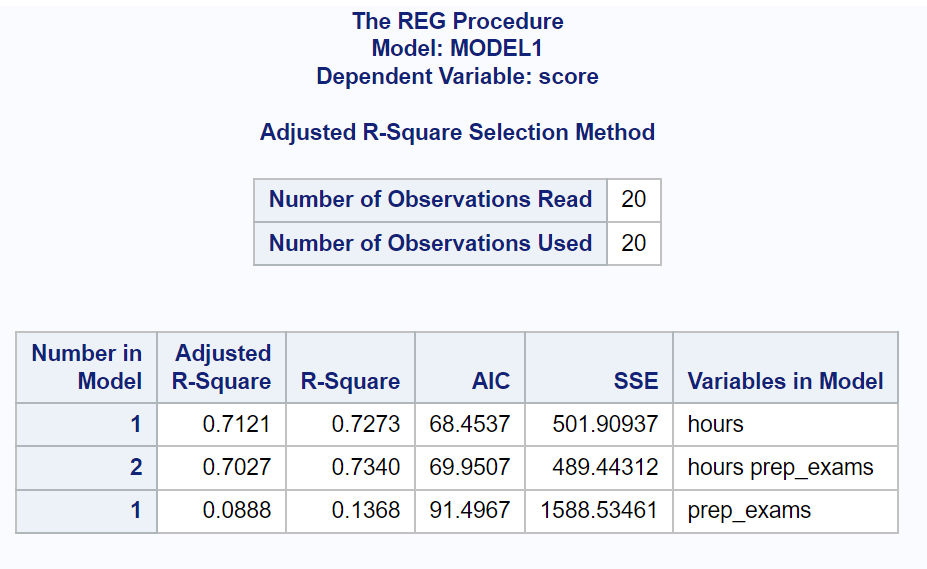
Dal risultato possiamo vedere i valori AIC per ciascun modello:

• AIC con ore come variabile predittiva: 68.4537
• AIC con ore ed esami come variabili predittive: 69.9507
• AIC con esami come variabile predittiva: 91.4967

Il modello con il valore AIC più basso è quello che contiene solo le ore come variabile predittiva.

Pertanto, dichiariamo che il seguente modello si adatta meglio ai dati:

Punteggio = β ₀ + β ₁ (ore studiate)

Una volta identificato questo modello come il migliore, possiamo adattarlo e analizzare i risultati, incluso il valore R quadrato e i coefficienti beta, per determinare l’esatta relazione tra le ore studiate e il voto dello studente. ‘esame finale.

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in SAS:

Come eseguire una regressione lineare semplice in SAS
Come eseguire la regressione lineare multipla in SAS
Come calcolare R quadrato in SAS
Come calcolare l’RMSE in SAS