Un'introduzione alla classificazione e agli alberi di regressione

Quando la relazione tra un insieme di variabili predittive e una variabile di risposta è lineare, metodi come la regressione lineare multipla possono produrre modelli predittivi accurati.

Tuttavia, quando la relazione tra un insieme di predittori e una risposta è altamente non lineare e complessa, i metodi non lineari possono funzionare meglio.

Un esempio di metodo non lineare sono gli alberi di classificazione e regressione , spesso abbreviati CART .

Come suggerisce il nome, i modelli CART utilizzano un insieme di variabili predittive per creare alberi decisionali che prevedono il valore di una variabile di risposta.

Ad esempio, supponiamo di avere un set di dati contenente le variabili predittive Anni giocati e Home Run medi e la variabile di risposta Stipendio annuale per centinaia di giocatori di baseball professionisti.

Ecco come potrebbe apparire un albero di regressione per questo set di dati:

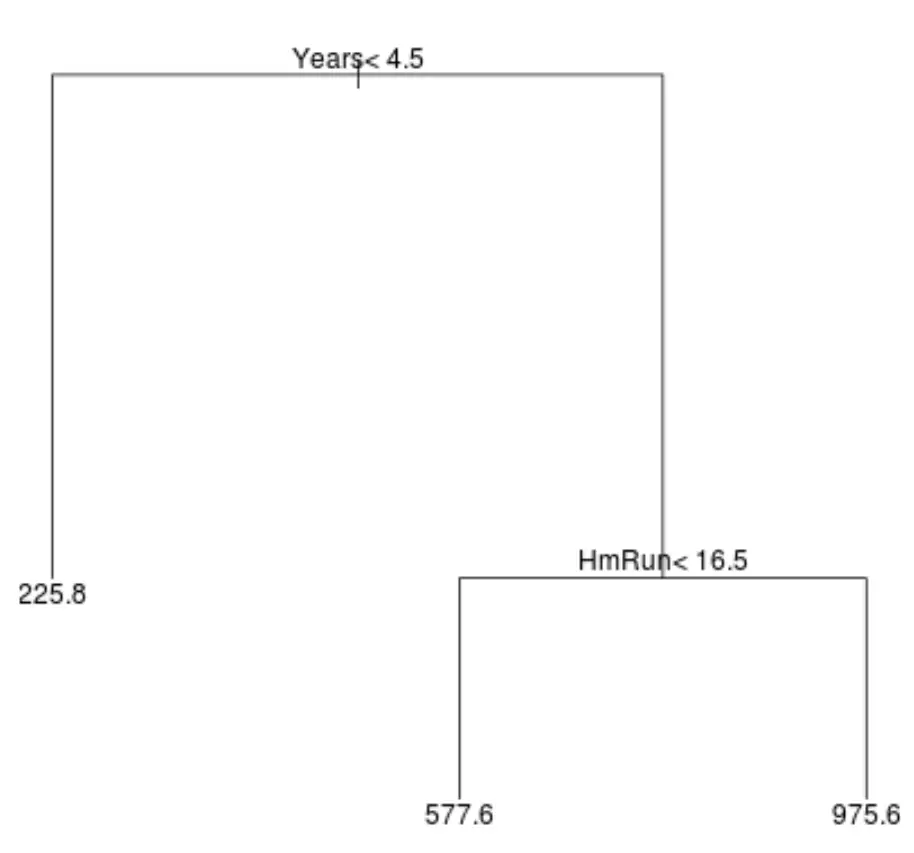
Il modo di interpretare l’albero è il seguente:

• I giocatori che hanno giocato meno di 4,5 anni hanno uno stipendio previsto di $ 225,8k.
• I giocatori che hanno giocato in media più di 4,5 anni o più e meno di 16,5 fuoricampo hanno uno stipendio previsto di $ 577,6K.
• I giocatori con 4,5 anni o più di esperienza di gioco e una media di 16,5 fuoricampo o più hanno uno stipendio previsto di $ 975,6K.

I risultati di questo modello dovrebbero intuitivamente avere senso: i giocatori con più anni di esperienza e più fuoricampo medi tendono a guadagnare stipendi più alti.

Possiamo quindi utilizzare questo modello per prevedere lo stipendio di un nuovo giocatore.

Ad esempio, supponiamo che un determinato giocatore abbia giocato 8 anni e abbia una media di 10 fuoricampo all’anno. Secondo il nostro modello, prevediamo che questo giocatore abbia uno stipendio annuo di $ 577,6k.

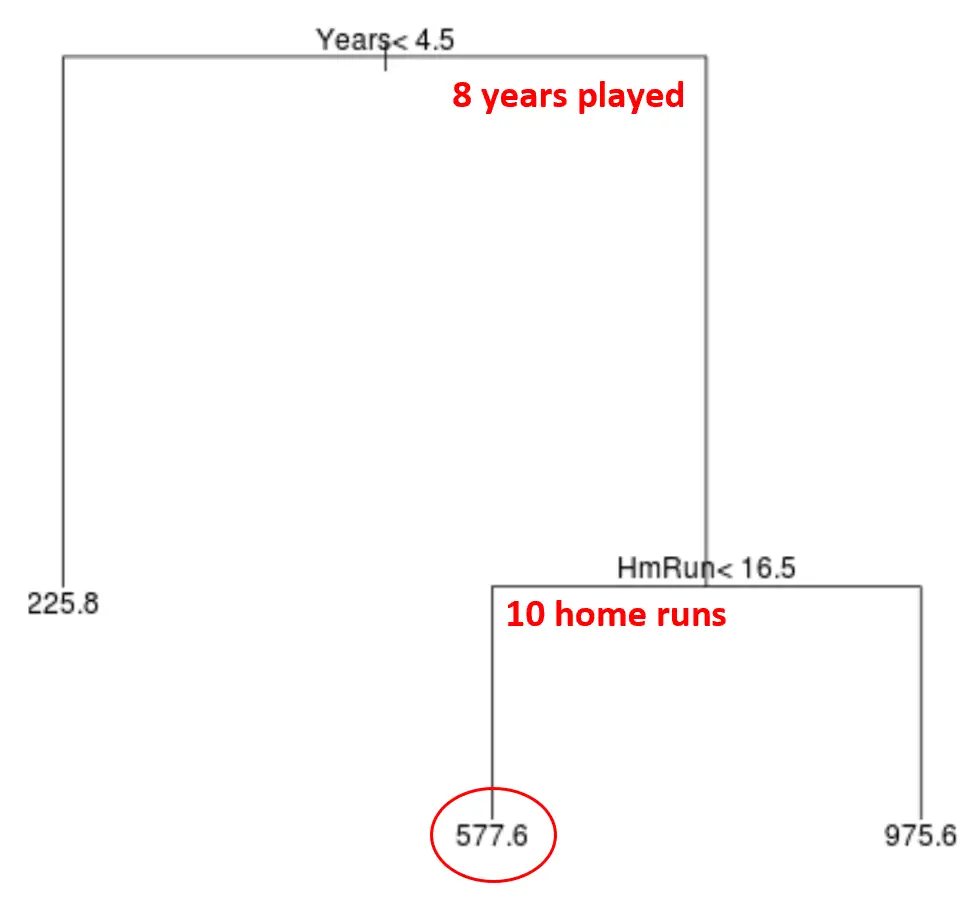
Alcune osservazioni sull’albero:

• La prima variabile predittiva situata in cima all’albero è la più importante, cioè quella che influenza maggiormente la previsione del valore della variabile di risposta. In questo caso gli anni giocati prevedono lo stipendio meglio della media dei circuiti .
• Le regioni alla base dell’albero sono chiamate nodi foglia . Questo particolare albero ha tre nodi terminali.

Passaggi per creare modelli CART

Possiamo utilizzare i seguenti passaggi per creare un modello CART per un determinato set di dati:

Passaggio 1: utilizzare la suddivisione binaria ricorsiva per far crescere un grande albero sui dati di training.

Innanzitutto, utilizziamo un algoritmo avido chiamato suddivisione binaria ricorsiva per far crescere un albero di regressione utilizzando il seguente metodo:

• Considerare tutte le variabili predittive X _{1 ,} X ₂ , … , errore standard residuo) quelle più basse. .
  • Per gli alberi di classificazione, scegliamo il predittore e il punto di taglio in modo tale che l’albero risultante abbia il tasso di errore di classificazione più basso.
• Ripetere questo processo, fermandosi solo quando ciascun nodo terminale ha meno di un certo numero minimo di osservazioni.

Questo algoritmo è avido perché in ogni fase del processo di costruzione dell’albero determina la migliore suddivisione da effettuare basandosi solo su quel passaggio, invece di guardare al futuro e scegliere una suddivisione che porterà a un albero globale migliore in una fase futura.

Passaggio 2: applicare la potatura della complessità dei costi all’albero di grandi dimensioni per ottenere una sequenza degli alberi migliori, basata su α.

Una volta cresciuto il grande albero, dobbiamo potarlo utilizzando un metodo noto come potatura complessa, che funziona come segue:

• Per ogni possibile albero con T nodi terminali, trovare l’albero che minimizza RSS + α|T|.
• Si noti che quando si aumenta il valore di α gli alberi con più nodi terminali risultano penalizzati. Ciò garantisce che l’albero non diventi troppo complesso.

Questo processo si traduce in una sequenza degli alberi migliori per ciascun valore di α.

Passaggio 3: utilizzare la convalida incrociata k-fold per scegliere α.

Una volta trovato l’albero migliore per ciascun valore di α, possiamo applicare la convalida incrociata k-fold per scegliere il valore di α che minimizza l’errore di test.

Passaggio 4: scegli il modello finale.

Infine, scegliamo il modello finale come quello che corrisponde al valore scelto di α.

Vantaggi e svantaggi dei modelli CART

I modelli CART offrono i seguenti vantaggi :

• Sono facili da interpretare.
• Sono facili da spiegare.
• Sono facili da visualizzare.
• Possono essere applicati sia a problemi di regressione che di classificazione .

Tuttavia, i modelli CART presentano i seguenti svantaggi:

• Tendono a non avere la stessa precisione predittiva di altri algoritmi di machine learning non lineari. Tuttavia, raggruppando molti alberi decisionali con metodi quali bagging, boosting e foreste casuali, è possibile migliorare la loro accuratezza predittiva.

Correlati: Come adattare gli alberi di classificazione e regressione in R