Come adattare gli alberi di classificazione e regressione in r

Quando la relazione tra un insieme di variabili predittive e una variabile di risposta è lineare, metodi come la regressione lineare multipla possono produrre modelli predittivi accurati.

Tuttavia, quando la relazione tra un insieme di predittori e una risposta è più complessa, i metodi non lineari possono spesso produrre modelli più accurati.

Uno di questi metodi è gli alberi di classificazione e regressione (CART), che utilizza un insieme di variabili predittive per creare alberi decisionali che prevedono il valore di una variabile di risposta.

Se la variabile di risposta è continua possiamo costruire alberi di regressione e se la variabile di risposta è categoriale possiamo costruire alberi di classificazione.

Questo tutorial spiega come creare alberi di regressione e classificazione in R.

Esempio 1: costruzione di un albero di regressione in R

Per questo esempio utilizzeremo il set di dati Hitters del pacchetto ISLR , che contiene varie informazioni su 263 giocatori di baseball professionisti.

Utilizzeremo questo set di dati per costruire un albero di regressione che utilizza le variabili predittive dei fuoricampo e degli anni giocati per prevedere lo stipendio di un determinato giocatore.

Utilizzare i passaggi seguenti per creare questo albero di regressione.

Passaggio 1: caricare i pacchetti necessari.

Innanzitutto, caricheremo i pacchetti necessari per questo esempio:

 library (ISLR) #contains Hitters dataset
library (rpart) #for fitting decision trees
library (rpart.plot) #for plotting decision trees

Passaggio 2: costruire l’albero di regressione iniziale.

Per prima cosa costruiremo un grande albero di regressione iniziale. Possiamo garantire che l’albero sia grande utilizzando un valore piccolo per cp , che sta per “parametro di complessità”.

Ciò significa che eseguiremo ulteriori suddivisioni sull’albero di regressione purché l’R quadrato complessivo del modello aumenti almeno del valore specificato da cp.

Utilizzeremo quindi la funzione printcp() per stampare i risultati del modello:

 #build the initial tree
tree <- rpart(Salary ~ Years + HmRun, data=Hitters, control=rpart. control (cp= .0001 ))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] HmRun Years

Root node error: 53319113/263 = 202734

n=263 (59 observations deleted due to missingness)

           CP nsplit rel error xerror xstd
1 0.24674996 0 1.00000 1.00756 0.13890
2 0.10806932 1 0.75325 0.76438 0.12828
3 0.01865610 2 0.64518 0.70295 0.12769
4 0.01761100 3 0.62652 0.70339 0.12337
5 0.01747617 4 0.60891 0.70339 0.12337
6 0.01038188 5 0.59144 0.66629 0.11817
7 0.01038065 6 0.58106 0.65697 0.11687
8 0.00731045 8 0.56029 0.67177 0.11913
9 0.00714883 9 0.55298 0.67881 0.11960
10 0.00708618 10 0.54583 0.68034 0.11988
11 0.00516285 12 0.53166 0.68427 0.11997
12 0.00445345 13 0.52650 0.68994 0.11996
13 0.00406069 14 0.52205 0.68988 0.11940
14 0.00264728 15 0.51799 0.68874 0.11916
15 0.00196586 16 0.51534 0.68638 0.12043
16 0.00016686 17 0.51337 0.67577 0.11635
17 0.00010000 18 0.51321 0.67576 0.11615
n=263 (59 observations deleted due to missingness)

Passaggio 3: potare l’albero.

Successivamente, sfoltiremo l’albero di regressione per trovare il valore ottimale da utilizzare per cp (il parametro di complessità) che porta all’errore di test più basso.

Si noti che il valore ottimale per cp è quello che porta all’errore x più basso nell’output precedente, che rappresenta l’errore sulle osservazioni dai dati di convalida incrociata.

 #identify best cp value to use
best <- tree$cptable[which. min (tree$cptable[," xerror "])," CP "]

#produce a pruned tree based on the best cp value
pruned_tree <- prune (tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen= 0 , #use full names for factor labels
    extra= 1 , #display number of obs. for each terminal node
    roundint= F , #don't round to integers in output
    digits= 5 ) #display 5 decimal places in output

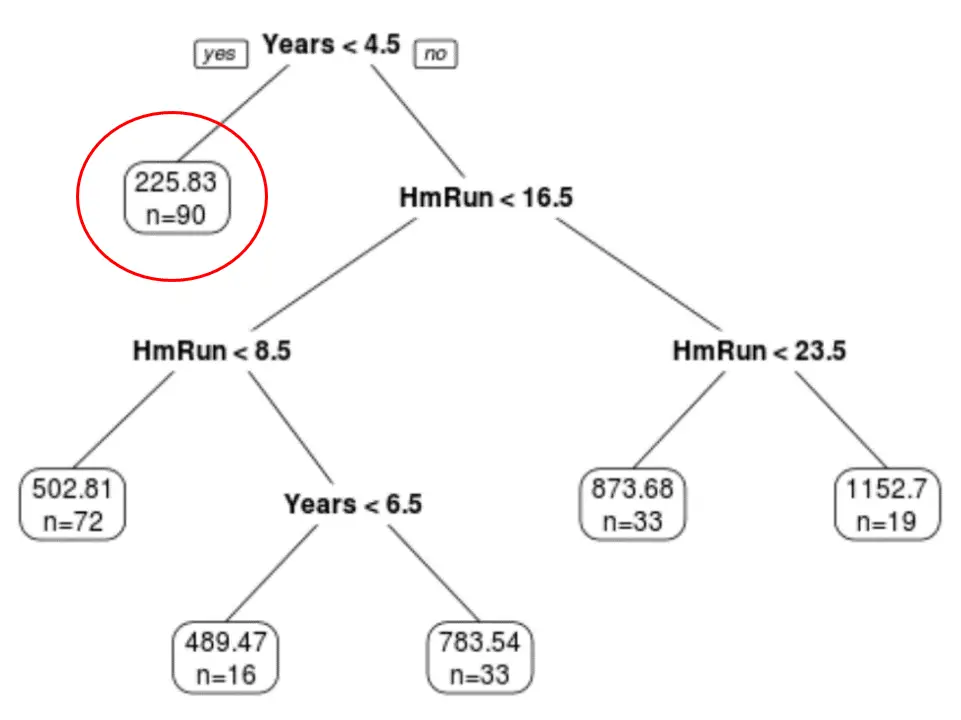
Possiamo vedere che l’albero finale potato ha sei nodi terminali. Ogni nodo foglia mostra lo stipendio previsto dei giocatori in quel nodo, nonché il numero di osservazioni del set di dati originale che appartengono a quel grado.

Ad esempio, possiamo vedere che nel set di dati originale c’erano 90 giocatori con meno di 4,5 anni di esperienza e il loro stipendio medio era di $ 225,83.000.

Passaggio 4: utilizzare l’albero per fare previsioni.

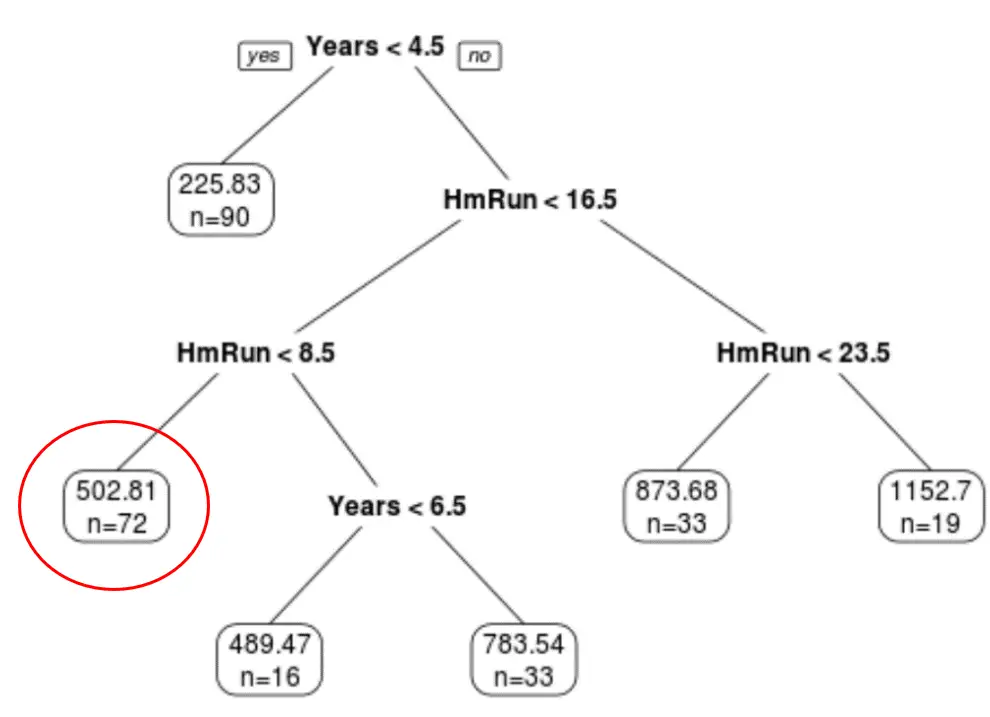
Possiamo utilizzare l’albero tagliato finale per prevedere lo stipendio di un determinato giocatore in base ai suoi anni di esperienza e ai fuoricampo medi.

Ad esempio, un giocatore che ha 7 anni di esperienza e 4 fuoricampo in media ha uno stipendio previsto di $ 502,81k .

Possiamo usare la funzione predit() in R per confermarlo:

 #define new player
new <- data.frame(Years=7, HmRun=4)

#use pruned tree to predict salary of this player
predict(pruned_tree, newdata=new)

502.8079

Esempio 2: costruzione di un albero di classificazione in R

Per questo esempio utilizzeremo il set di dati ptitanic del pacchetto rpart.plot , che contiene varie informazioni sui passeggeri a bordo del Titanic.

Utilizzeremo questo set di dati per creare un albero di classificazione che utilizza le variabili predittive classe , sesso ed età per prevedere se un determinato passeggero è sopravvissuto o meno.

Utilizzare i passaggi seguenti per creare questo albero di classificazione.

Passaggio 1: caricare i pacchetti necessari.

Innanzitutto, caricheremo i pacchetti necessari per questo esempio:

 library (rpart) #for fitting decision trees
library (rpart.plot) #for plotting decision trees

Passaggio 2: costruire l’albero di classificazione iniziale.

Per prima cosa costruiremo un grande albero di classificazione iniziale. Possiamo garantire che l’albero sia grande utilizzando un valore piccolo per cp , che sta per “parametro di complessità”.

Ciò significa che eseguiremo ulteriori suddivisioni sull’albero di classificazione purché l’adattamento complessivo del modello aumenti almeno del valore specificato da cp.

Utilizzeremo quindi la funzione printcp() per stampare i risultati del modello:

 #build the initial tree
tree <- rpart(survived~pclass+sex+age, data=ptitanic, control=rpart. control (cp= .0001 ))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] age pclass sex   

Root node error: 500/1309 = 0.38197

n=1309 

      CP nsplit rel error xerror xstd
1 0.4240 0 1.000 1.000 0.035158
2 0.0140 1 0.576 0.576 0.029976
3 0.0095 3 0.548 0.578 0.030013
4 0.0070 7 0.510 0.552 0.029517
5 0.0050 9 0.496 0.528 0.029035
6 0.0025 11 0.486 0.532 0.029117
7 0.0020 19 0.464 0.536 0.029198
8 0.0001 22 0.458 0.528 0.029035

Passaggio 3: potare l’albero.

Successivamente, sfoltiremo l’albero di regressione per trovare il valore ottimale da utilizzare per cp (il parametro di complessità) che porta all’errore di test più basso.

Si noti che il valore ottimale per cp è quello che porta all’errore x più basso nell’output precedente, che rappresenta l’errore sulle osservazioni dai dati di convalida incrociata.

 #identify best cp value to use
best <- tree$cptable[which. min (tree$cptable[," xerror "])," CP "]

#produce a pruned tree based on the best cp value
pruned_tree <- prune (tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen= 0 , #use full names for factor labels
    extra= 1 , #display number of obs. for each terminal node
    roundint= F , #don't round to integers in output
    digits= 5 ) #display 5 decimal places in output

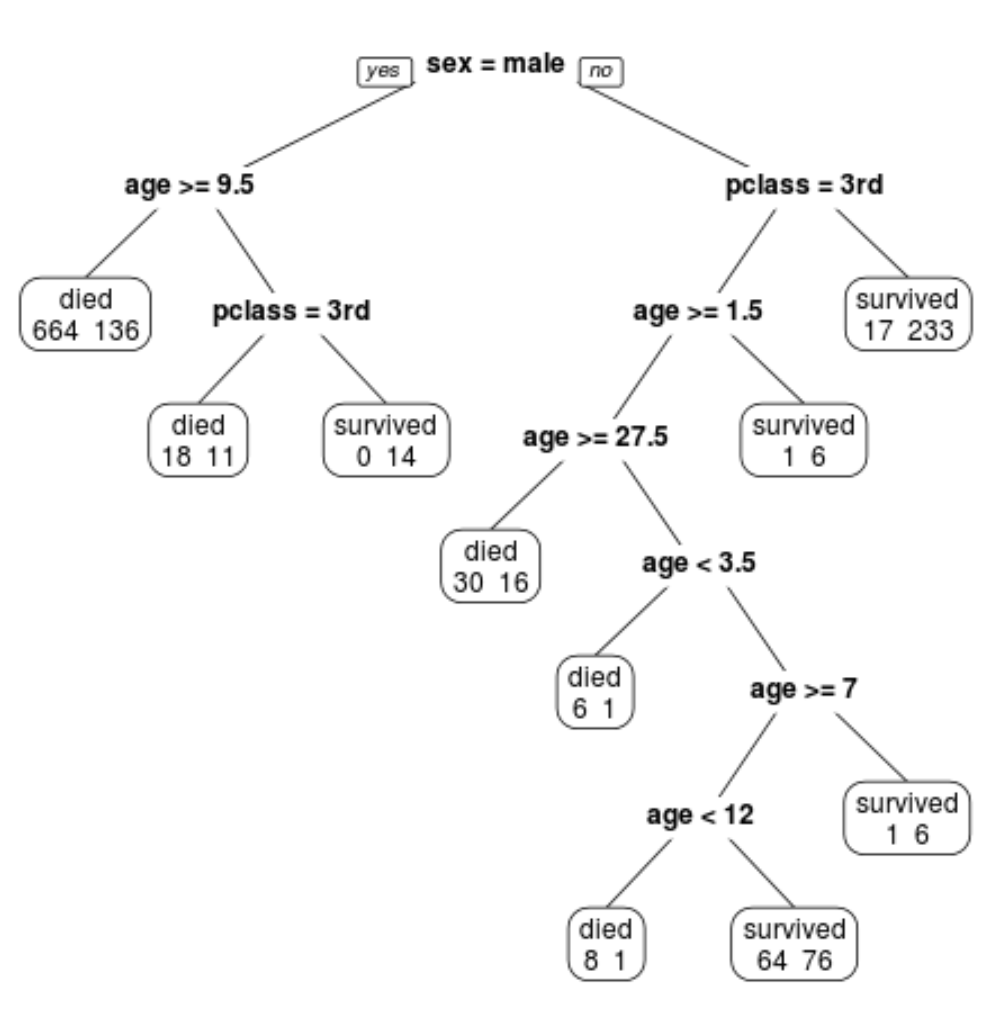
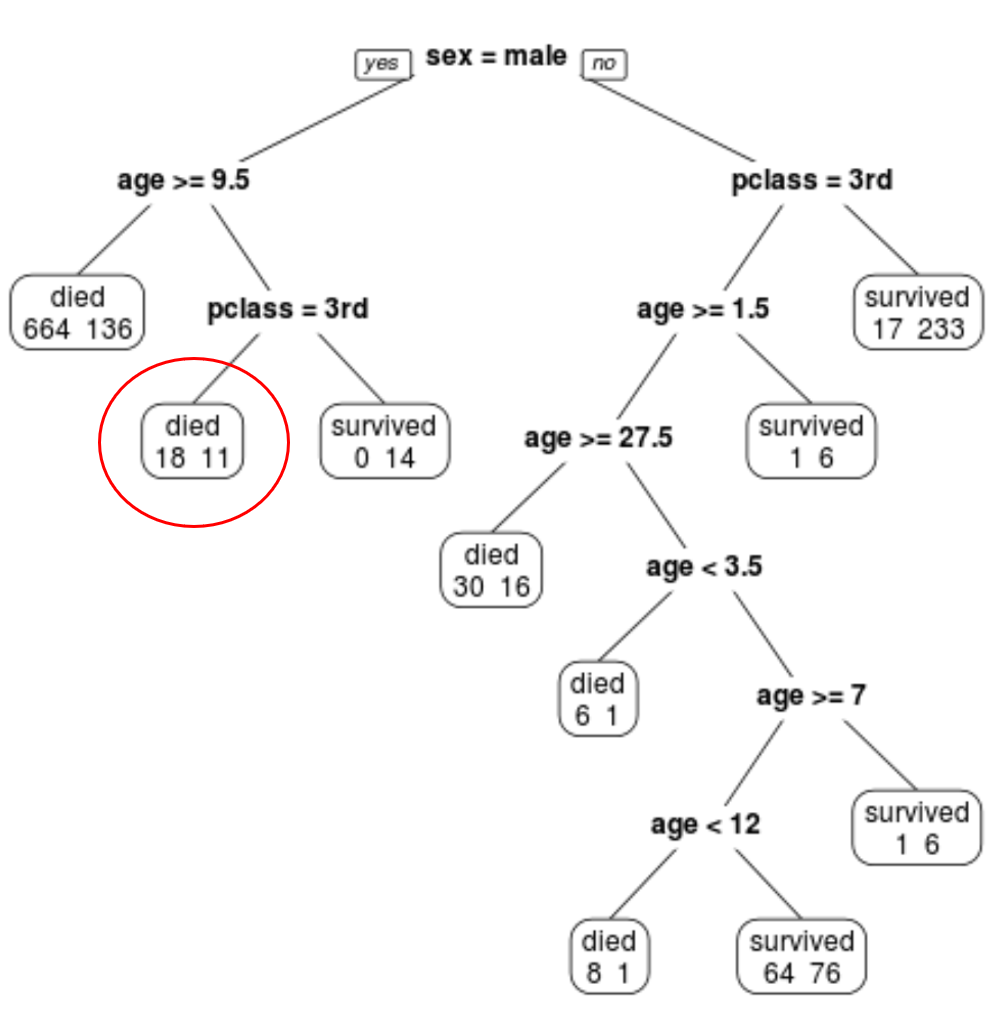
Possiamo vedere che l’albero finale potato ha 10 nodi terminali. Ogni nodo terminale indica il numero di passeggeri deceduti nonché il numero di sopravvissuti.

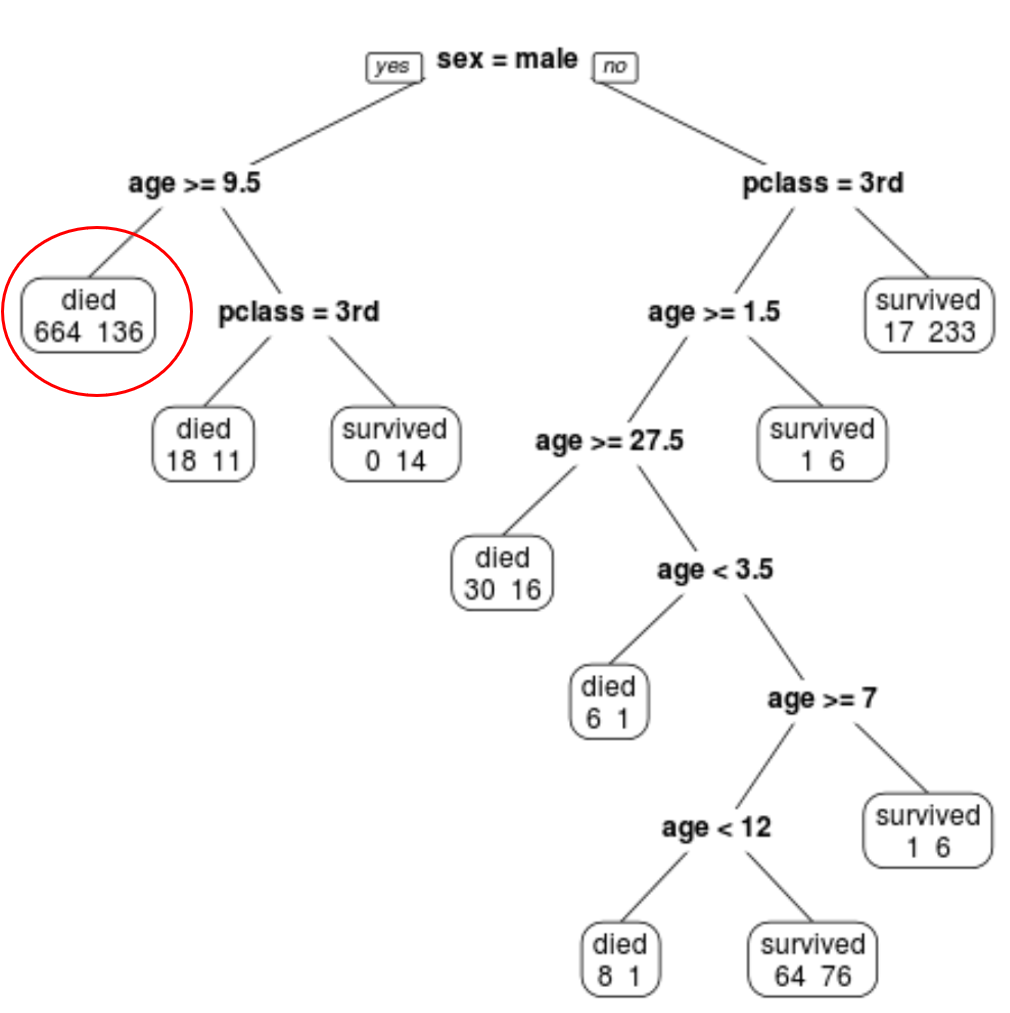
Ad esempio, nel nodo più a sinistra vediamo che 664 passeggeri sono morti e 136 sono sopravvissuti.

Passaggio 4: utilizzare l’albero per fare previsioni.

Possiamo utilizzare l’albero tagliato finale per prevedere la probabilità che un dato passeggero sopravviva in base alla sua classe, età e sesso.

Ad esempio, un passeggero maschio di 8 anni e in 1a classe ha una probabilità di sopravvivenza di 29/11 = 37,9%.

È possibile trovare il codice R completo utilizzato in questi esempi qui .