Come eseguire l'analisi bivariata in r (con esempi)

Il termine analisi bivariata si riferisce all’analisi di due variabili. Puoi ricordarlo perché il prefisso “bi” significa “due”.

L’obiettivo dell’analisi bivariata è comprendere la relazione tra due variabili

Esistono tre modi comuni per eseguire l’analisi bivariata:

1. Nuvole di punti

2. Coefficienti di correlazione

3. Regressione lineare semplice

L’esempio seguente mostra come eseguire ciascuno di questi tipi di analisi bivariata utilizzando il seguente set di dati che contiene informazioni su due variabili: (1) Ore trascorse a studiare e (2) Punteggi dei test ottenuti da 20 studenti diversi:

 #create data frame
df <- data. frame (hours=c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                         3, 4, 4, 5, 5, 6, 6, 6, 7, 8),
                 score=c(75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                         80, 88, 85, 90, 92, 94, 94, 88, 91, 96))

#view first six rows of data frame
head(df)

  hours score
1 1 75
2 1 66
3 1 68
4 2 74
5 2 78
6 2 72

1. Nuvole di punti

Possiamo utilizzare la seguente sintassi per creare un grafico a dispersione delle ore studiate rispetto al voto dell’esame in R:

 #create scatterplot of hours studied vs. exam score
plot(df$hours, df$score, pch= 16 , col=' steelblue ',
     main=' Hours Studied vs. Exam Score ',
     xlab=' Hours Studied ', ylab=' Exam Score ')

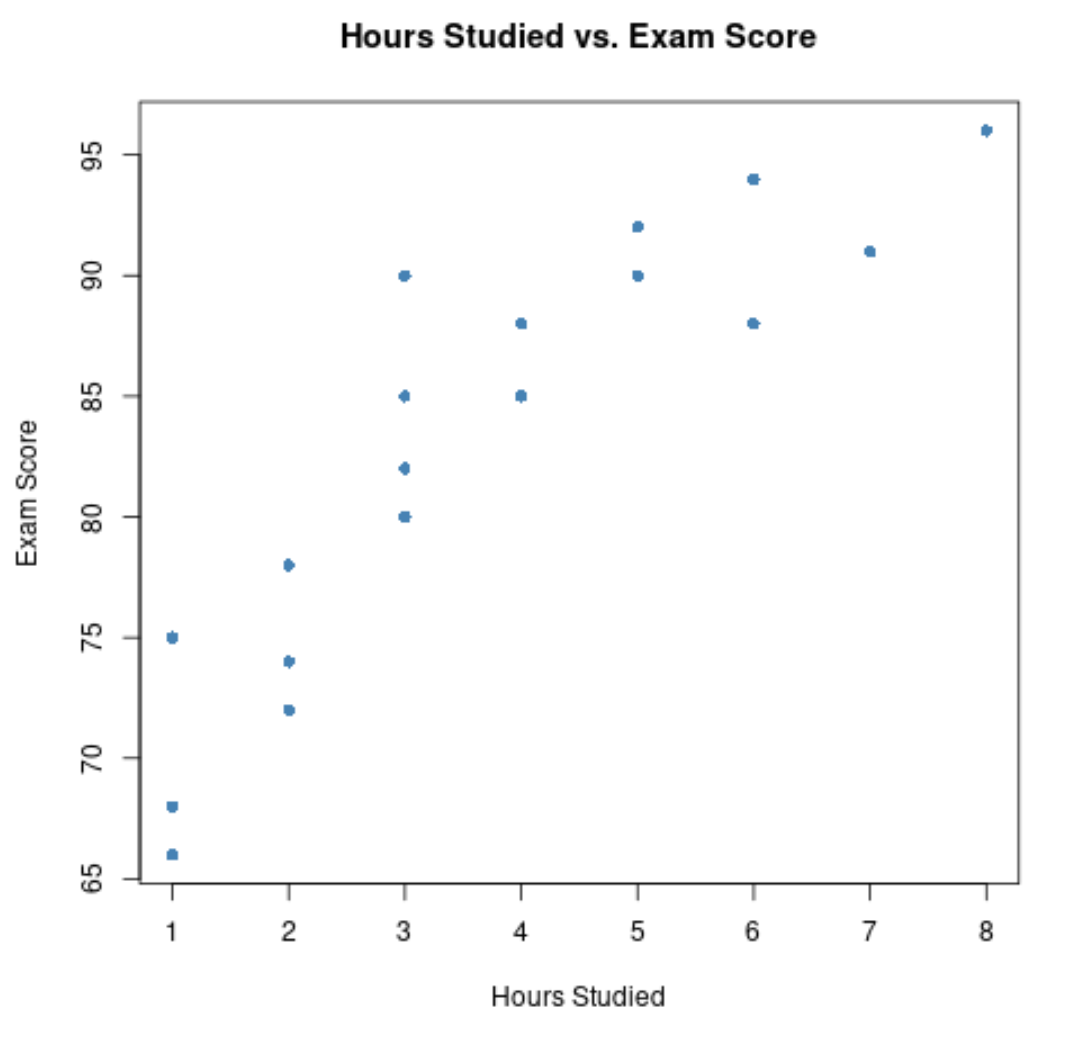
L’asse x mostra le ore studiate e l’asse y mostra il voto ottenuto all’esame.

Dal grafico emerge che esiste una relazione positiva tra le due variabili: all’aumentare del numero di ore di studio, anche i punteggi degli esami tendono ad aumentare.

2. Coefficienti di correlazione

Un coefficiente di correlazione di Pearson è un modo per quantificare la relazione lineare tra due variabili.

Possiamo usare la funzione cor() in R per calcolare il coefficiente di correlazione di Pearson tra due variabili:

 #calculate correlation between hours studied and exam score received
cor(df$hours, df$score)

[1] 0.891306

Il coefficiente di correlazione risulta essere 0,891 .

Questo valore è prossimo a 1, indicando una forte correlazione positiva tra ore studiate e voto dell’esame.

3. Regressione lineare semplice

La regressione lineare semplice è un metodo statistico che possiamo utilizzare per trovare l’equazione della linea che meglio “si adatta” a un insieme di dati, che possiamo quindi utilizzare per comprendere l’esatta relazione tra due variabili.

Possiamo utilizzare la funzione lm() in R per adattare un semplice modello di regressione lineare per le ore studiate e i risultati degli esami ricevuti:

 #fit simple linear regression model
fit <- lm(score ~ hours, data=df)

#view summary of model
summary(fit)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min 1Q Median 3Q Max 
-6,920 -3,927 1,309 1,903 9,385 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 69.0734 1.9651 35.15 < 2nd-16 ***
hours 3.8471 0.4613 8.34 1.35e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.171 on 18 degrees of freedom
Multiple R-squared: 0.7944, Adjusted R-squared: 0.783 
F-statistic: 69.56 on 1 and 18 DF, p-value: 1.347e-07

L’equazione di regressione adattata risulta essere:

Punteggio esame = 69,0734 + 3,8471*(ore studiate)

Questo ci dice che ogni ora aggiuntiva studiata è associata a un aumento medio di 3,8471 nel punteggio dell’esame.

Possiamo anche utilizzare l’equazione di regressione adattata per prevedere il punteggio che uno studente riceverà in base al numero totale di ore studiate.

Ad esempio, uno studente che studia per 3 ore dovrebbe ottenere un punteggio di 81.6147 :

• Punteggio esame = 69,0734 + 3,8471*(ore studiate)
• Punteggio dell’esame = 69,0734 + 3,8471*(3)
• Risultato dell’esame = 81.6147

Risorse addizionali

Le seguenti esercitazioni forniscono informazioni aggiuntive sull’analisi bivariata:

Un’introduzione all’analisi bivariata
5 esempi di dati bivariati nella vita reale
Un’introduzione alla regressione lineare semplice