Analisi delle componenti principali in r: esempio passo passo

L’analisi delle componenti principali, spesso abbreviata PCA, è una tecnica di apprendimento automatico non supervisionata che cerca di trovare le componenti principali – combinazioni lineari dei predittori originali – che spiegano gran parte della variazione in un set di dati.

L’obiettivo della PCA è spiegare la maggior parte della variabilità in un set di dati con meno variabili rispetto al set di dati originale.

Per un dato set di dati con variabili p , potremmo esaminare i grafici a dispersione di ciascuna combinazione di variabili a coppie, ma il numero di grafici a dispersione può aumentare molto rapidamente.

Per i predittori p esistono nuvole di punti p(p-1)/2.

Quindi, per un set di dati con p = 15 predittori, ci sarebbero 105 diversi grafici a dispersione!

Fortunatamente, la PCA offre un modo per trovare una rappresentazione a bassa dimensionalità di un set di dati che catturi la maggior quantità possibile di variazioni nei dati.

Se riuscissimo a catturare la maggior parte della variazione in sole due dimensioni, potremmo proiettare tutte le osservazioni del set di dati originale su un semplice grafico a dispersione.

Il modo in cui troviamo i componenti principali è il seguente:

_{Dato un set di dati con} p _predittori : _

• _{Z m = ΣΦ jm _}
• Z ₁ è la combinazione lineare di predittori che cattura quanta più varianza possibile.
• Z ₂ è la successiva combinazione lineare di predittori che cattura la maggior varianza pur essendo ortogonale (cioè non correlata) a Z ₁ .
• Z ₃ è quindi la successiva combinazione lineare di predittori che cattura la maggiore varianza pur essendo ortogonale a Z ₂ .
• E così via.

In pratica, utilizziamo i seguenti passaggi per calcolare le combinazioni lineari dei predittori originali:

1. Scala ciascuna variabile in modo che abbia una media pari a 0 e una deviazione standard pari a 1.

2. Calcolare la matrice di covarianza per le variabili scalate.

3. Calcola gli autovalori della matrice di covarianza.

Utilizzando l’algebra lineare, possiamo dimostrare che l’autovettore che corrisponde all’autovalore più grande è la prima componente principale. In altre parole, questa particolare combinazione di predittori spiega la maggiore varianza nei dati.

L’autovettore corrispondente al secondo autovalore più grande è la seconda componente principale e così via.

Questo tutorial fornisce un esempio passo passo di come eseguire questo processo in R.

Passaggio 1: caricare i dati

Per prima cosa caricheremo il pacchetto Tidyverse , che contiene diverse funzioni utili per visualizzare e manipolare i dati:

 library (tidyverse)

Per questo esempio, utilizzeremo il set di dati USArrests integrato in R, che contiene il numero di arresti per 100.000 residenti in ciascuno stato degli Stati Uniti nel 1973 per omicidio , aggressione e stupro .

Include anche la percentuale della popolazione di ciascuno stato che vive in aree urbane, UrbanPop .

Il codice seguente mostra come caricare e visualizzare le prime righe del set di dati:

 #load data
data ("USArrests")

#view first six rows of data
head(USArrests)

           Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
Arkansas 8.8 190 50 19.5
California 9.0 276 91 40.6
Colorado 7.9 204 78 38.7

Passaggio 2: calcolare i componenti principali

Dopo aver caricato i dati, possiamo utilizzare la funzione integrata prcomp() di R per calcolare i componenti principali del set di dati.

Assicurati di specificare scale = TRUE in modo che ciascuna delle variabili nel set di dati venga ridimensionata per avere una media pari a 0 e una deviazione standard pari a 1 prima di calcolare i componenti principali.

Si noti inoltre che gli autovettori in R puntano nella direzione negativa per impostazione predefinita, quindi moltiplicheremo per -1 per invertire i segni.

 #calculate main components
results <- prcomp(USArrests, scale = TRUE )

#reverse the signs
results$rotation <- -1*results$rotation

#display main components
results$rotation

               PC1 PC2 PC3 PC4
Murder 0.5358995 -0.4181809 0.3412327 -0.64922780
Assault 0.5831836 -0.1879856 0.2681484 0.74340748
UrbanPop 0.2781909 0.8728062 0.3780158 -0.13387773
Rape 0.5434321 0.1673186 -0.8177779 -0.08902432

Possiamo vedere che la prima componente principale (PC1) ha valori elevati per omicidio, aggressione e stupro, indicando che questa componente principale descrive la variazione maggiore in queste variabili.

Possiamo anche vedere che la seconda componente principale (PC2) ha un valore elevato per UrbanPop, indicando che questa componente principale enfatizza la popolazione urbana.

Tieni presente che i punteggi dei componenti principali per ciascuno stato sono archiviati in results$x . Moltiplicheremo anche questi punteggi per -1 per invertire i segni:

 #reverse the signs of the scores
results$x <- -1*results$x

#display the first six scores
head(results$x)

                  PC1 PC2 PC3 PC4
Alabama 0.9756604 -1.1220012 0.43980366 -0.154696581
Alaska 1.9305379 -1.0624269 -2.01950027 0.434175454
Arizona 1.7454429 0.7384595 -0.05423025 0.826264240
Arkansas -0.1399989 -1.1085423 -0.11342217 0.180973554
California 2.4986128 1.5274267 -0.59254100 0.338559240
Colorado 1.4993407 0.9776297 -1.08400162 -0.001450164

Passaggio 3: Visualizza i risultati con un biplot

Successivamente, possiamo creare un biplot , un grafico che proietta ciascuna delle osservazioni nel set di dati su un grafico a dispersione che utilizza la prima e la seconda componente principale come assi:

Si noti che scale = 0 garantisce che le frecce nel grafico siano ridimensionate per rappresentare i carichi.

 biplot(results, scale = 0 )

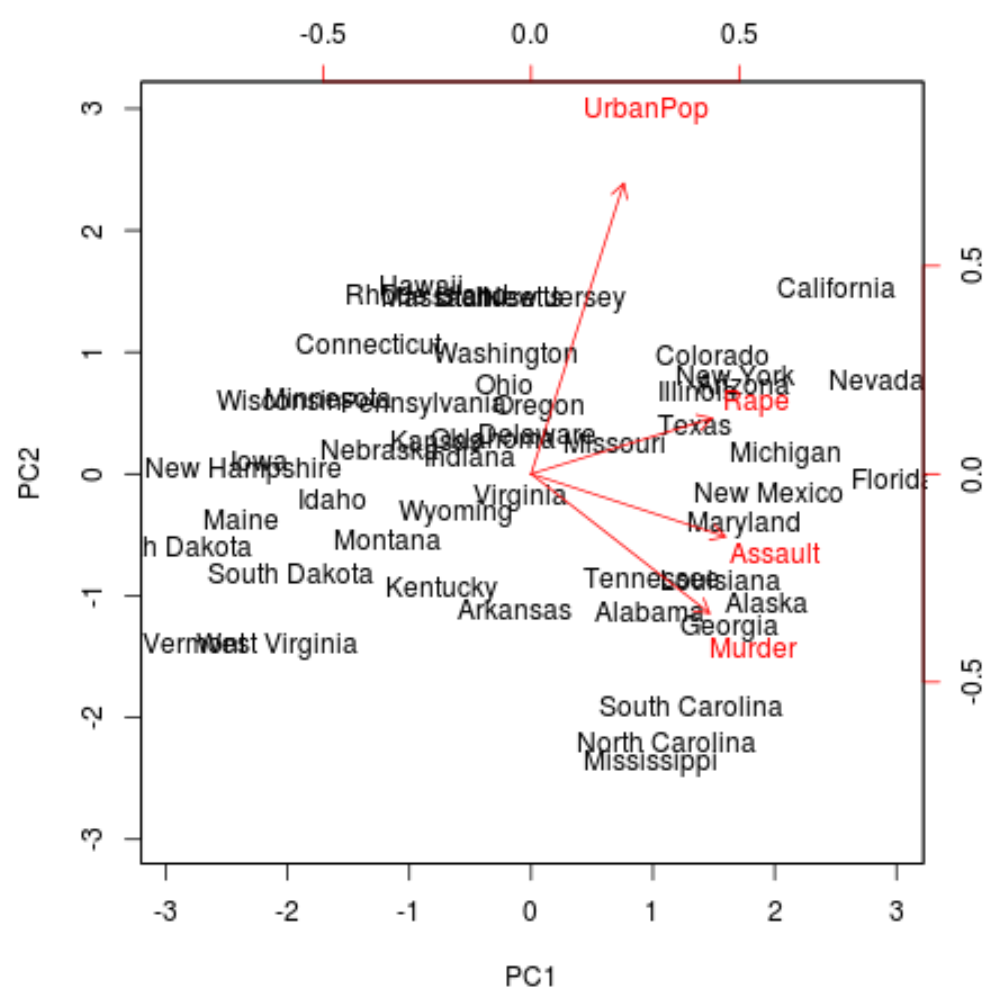
Dalla trama possiamo vedere ciascuno dei 50 stati rappresentati in un semplice spazio bidimensionale.

Gli stati vicini tra loro nel grafico hanno modelli di dati simili rispetto alle variabili nel set di dati originale.

Possiamo anche vedere che alcuni stati sono più fortemente associati a determinati crimini rispetto ad altri. Ad esempio, la Georgia è lo stato più vicino alla variabile Omicidio nella trama.

Se guardiamo gli stati con il tasso di omicidi più alto nel set di dati originale, possiamo vedere che la Georgia è effettivamente in cima alla lista:

 #display states with highest murder rates in original dataset
head(USArrests[ order (-USArrests$Murder),])

               Murder Assault UrbanPop Rape
Georgia 17.4 211 60 25.8
Mississippi 16.1 259 44 17.1
Florida 15.4 335 80 31.9
Louisiana 15.4 249 66 22.2
South Carolina 14.4 279 48 22.5
Alabama 13.2 236 58 21.2

Passaggio 4: Trova la varianza spiegata da ciascuna componente principale

Possiamo utilizzare il seguente codice per calcolare la varianza totale nel set di dati originale spiegata da ciascuna componente principale:

 #calculate total variance explained by each principal component
results$sdev^2 / sum (results$sdev^2)

[1] 0.62006039 0.24744129 0.08914080 0.04335752

Dai risultati possiamo osservare quanto segue:

• La prima componente principale spiega il 62% della varianza totale nel set di dati.
• La seconda componente principale spiega il 24,7% della varianza totale nel set di dati.
• La terza componente principale spiega l’ 8,9% della varianza totale nel set di dati.
• La quarta componente principale spiega il 4,3% della varianza totale nel set di dati.

Pertanto, le prime due componenti principali spiegano la maggior parte della varianza totale dei dati.

Questo è un buon segno perché il biplot precedente proiettava ciascuna delle osservazioni dei dati originali su un grafico a dispersione che teneva conto solo delle prime due componenti principali.

Pertanto, è valido esaminare i modelli nel biplot per identificare stati simili tra loro.

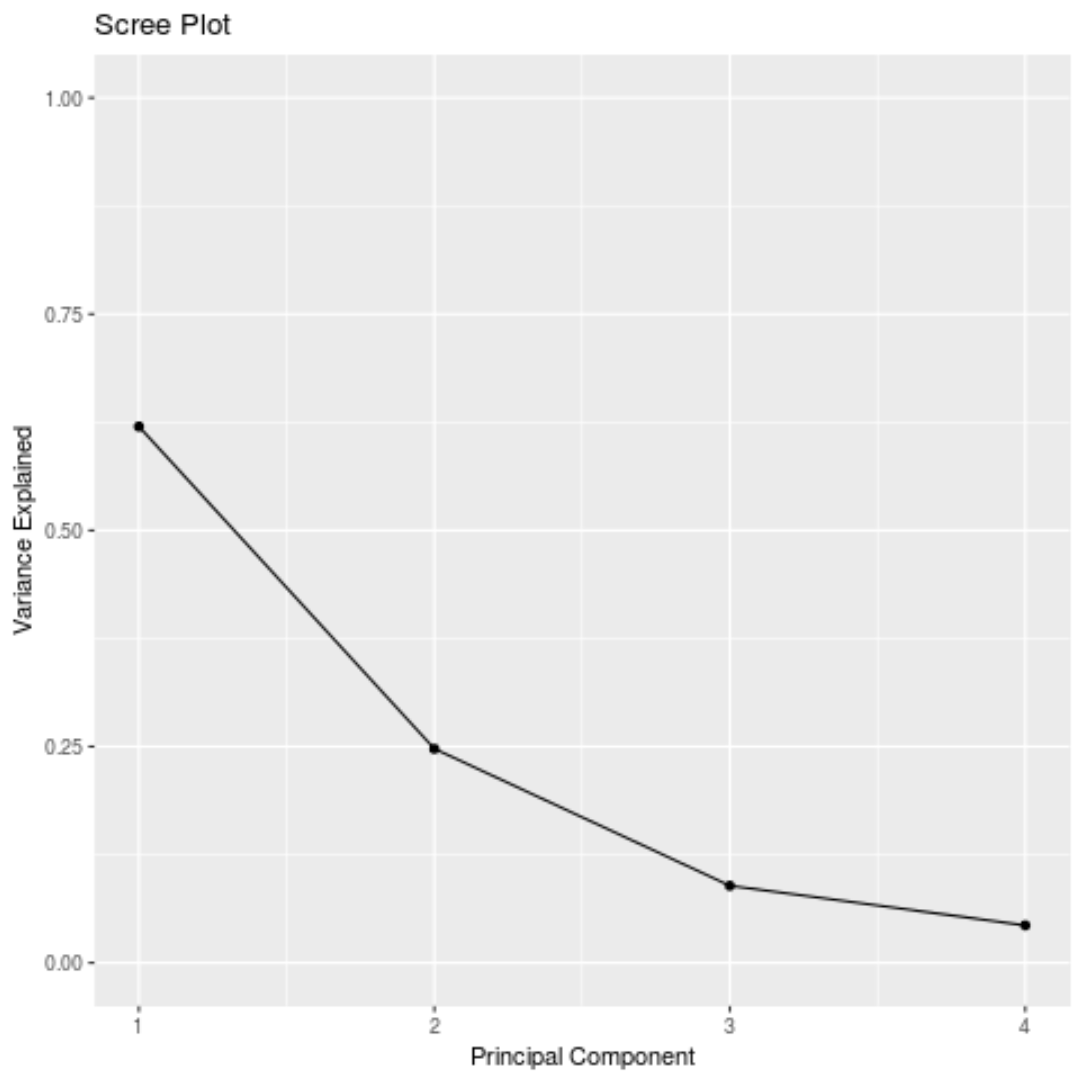
Possiamo anche creare uno scree plot – un grafico che mostra la varianza totale spiegata da ciascun componente principale – per visualizzare i risultati della PCA:

 #calculate total variance explained by each principal component
var_explained = results$sdev^2 / sum (results$sdev^2)

#create scree plot
qplot(c(1:4), var_explained) + 
  geom_line() + 
  xlab(" Principal Component ") + 
  ylab(" Variance Explained ") +
  ggtitle(" Scree Plot ") +
  ylim(0, 1) 

Analisi delle componenti principali nella pratica

In pratica, la PCA viene utilizzata più spesso per due motivi:

1. Analisi esplorativa dei dati : utilizziamo la PCA quando esploriamo per la prima volta un set di dati e vogliamo capire quali osservazioni nei dati sono più simili tra loro.

2. Regressione delle componenti principali – Possiamo anche utilizzare la PCA per calcolare le componenti principali che possono poi essere utilizzate nella regressione delle componenti principali . Questo tipo di regressione viene spesso utilizzato quando è presente multicollinearità tra i predittori in un set di dati.

Il codice R completo utilizzato in questo tutorial può essere trovato qui .