Come eseguire l'analisi dei componenti principali in sas

L’analisi delle componenti principali (PCA) è una tecnica di apprendimento automatico non supervisionata che cerca di trovare le componenti principali – combinazioni lineari di variabili predittive – che spiegano gran parte della variazione in un set di dati.

Il modo più semplice per eseguire PCA in SAS è utilizzare l’istruzione PROC PRINCOMP , che utilizza la seguente sintassi di base:

 proc princomp data =my_data out =out_data outstat =stats;
    var var1 var2 var3;
run ;

Ecco cosa fa ciascuna istruzione:

• data : il nome del set di dati da utilizzare per la PCA
• out : il nome del set di dati da creare che contiene tutti i dati originali più i punteggi dei componenti principali
• outstat : specifica che deve essere creato un set di dati contenente medie, deviazioni standard, coefficienti di correlazione, autovalori e autovettori.
• var : le variabili da utilizzare per PCA dal set di dati di input.

Il seguente esempio passo passo mostra come utilizzare in pratica l’istruzione PROC PRINCOMP per eseguire l’analisi dei componenti principali in SAS.

Passaggio 1: crea un set di dati

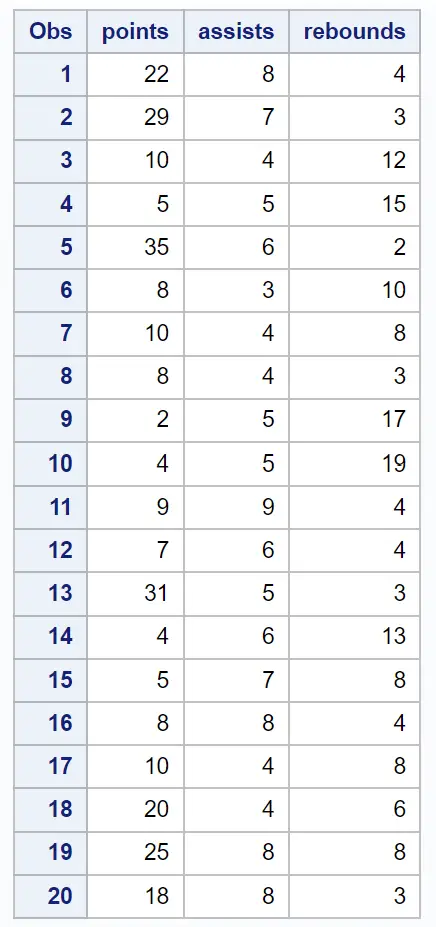
Supponiamo di avere il seguente set di dati contenente varie informazioni su 20 giocatori di basket:

 /*create dataset*/
data my_data;
    input points assists rebounds;
    datalines ;
22 8 4
29 7 3
10 4 12
5 5 15
35 6 2
8 3 10
10 4 8
8 4 3
2 5 17
4 5 19
9 9 4
7 6 4
31 5 3
4 6 13
5 7 8
8 8 4
10 4 8
20 4 6
25 8 8
18 8 3
;
run ;

/*view dataset*/
proc print data =my_data; 

Passaggio 2: eseguire l’analisi delle componenti principali

Possiamo utilizzare l’istruzione PROC PRINCOMP per eseguire l’analisi delle componenti principali utilizzando le variabili points , assist e rimbalzi del set di dati:

 /*perform principal components analysis*/
proc princomp data =my_data out =out_data outstat =stats;
    var points assists rebounds;
run ;

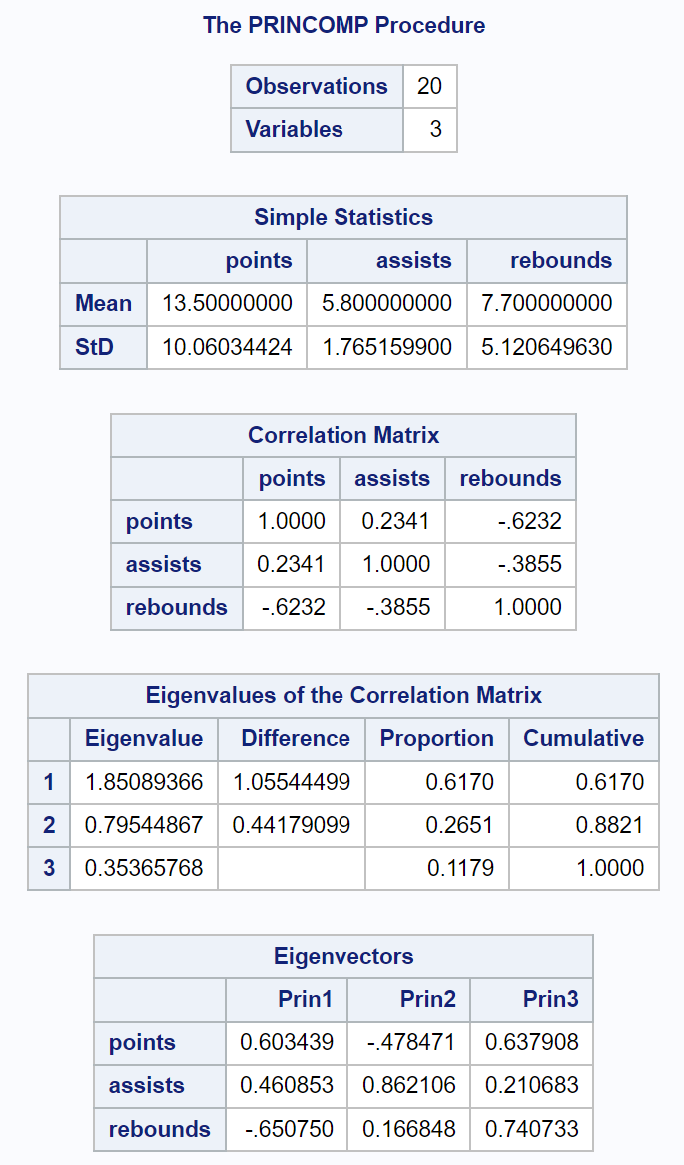
La prima parte dell’output mostra varie statistiche descrittive, tra cui la media e le deviazioni standard di ciascuna variabile di input, una matrice di correlazione e i valori degli autovalori e degli autovettori:

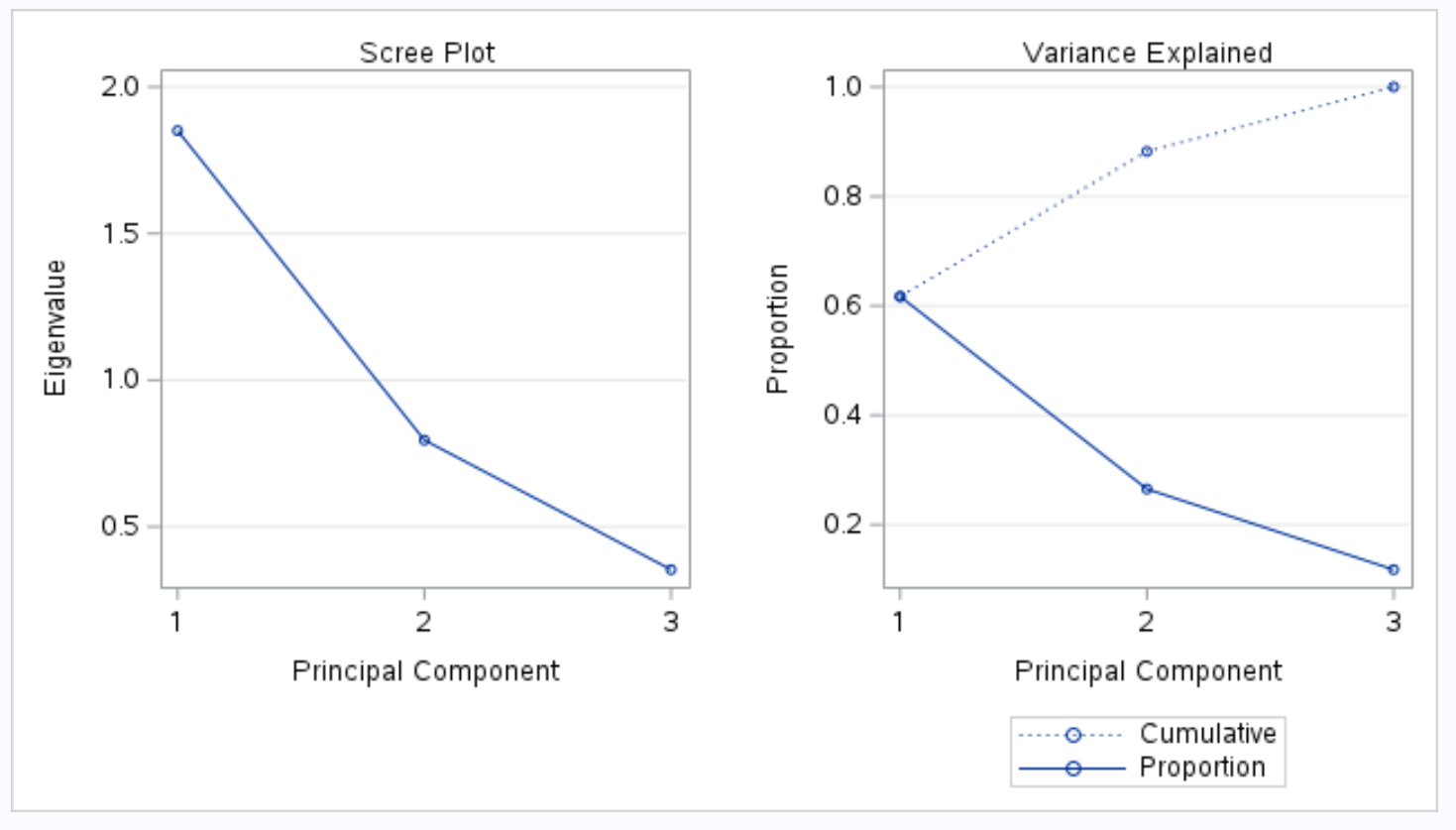
La parte successiva dell’output mostra uno scree plot e un grafico della varianza spiegato :

Quando eseguiamo la PCA, spesso vogliamo capire quale percentuale della variazione totale nel set di dati può essere spiegata da ciascun componente principale.

La tabella risultante intitolata Autovalori della matrice di correlazione ci consente di vedere esattamente quale percentuale della variazione totale è spiegata da ciascuna componente principale:

• La prima componente principale spiega il 61,7% della variazione totale del set di dati.
• La seconda componente principale spiega il 26,51% della variazione totale del set di dati.
• La terza componente principale spiega l’ 11,79% della variazione totale nel set di dati.

Tieni presente che tutte le percentuali ammontano a 100%.

Il grafico intitolato Variance Explained ci consente quindi di visualizzare questi valori.

L’asse x mostra la componente principale e l’asse y mostra la percentuale della varianza totale spiegata da ogni singola componente principale.

Passaggio 3: crea un biplot per visualizzare i risultati

Per visualizzare i risultati della PCA per un dato set di dati, possiamo creare un biplot , ovvero un grafico che mostra ciascuna osservazione in un set di dati su un piano formato dai primi due componenti principali.

Possiamo usare la seguente sintassi in SAS per creare un biplot:

 /*create dataset with column called obs to represent row numbers of original data*/
data biplot_data;
   set out_data;
   obs=_n_;
run ;

/*create biplot using values from first two principal components*/
proc sgplot data =biplot_data;
    scatter x =Prin1 y =Prin2 / datalabel =obs;
run ; 

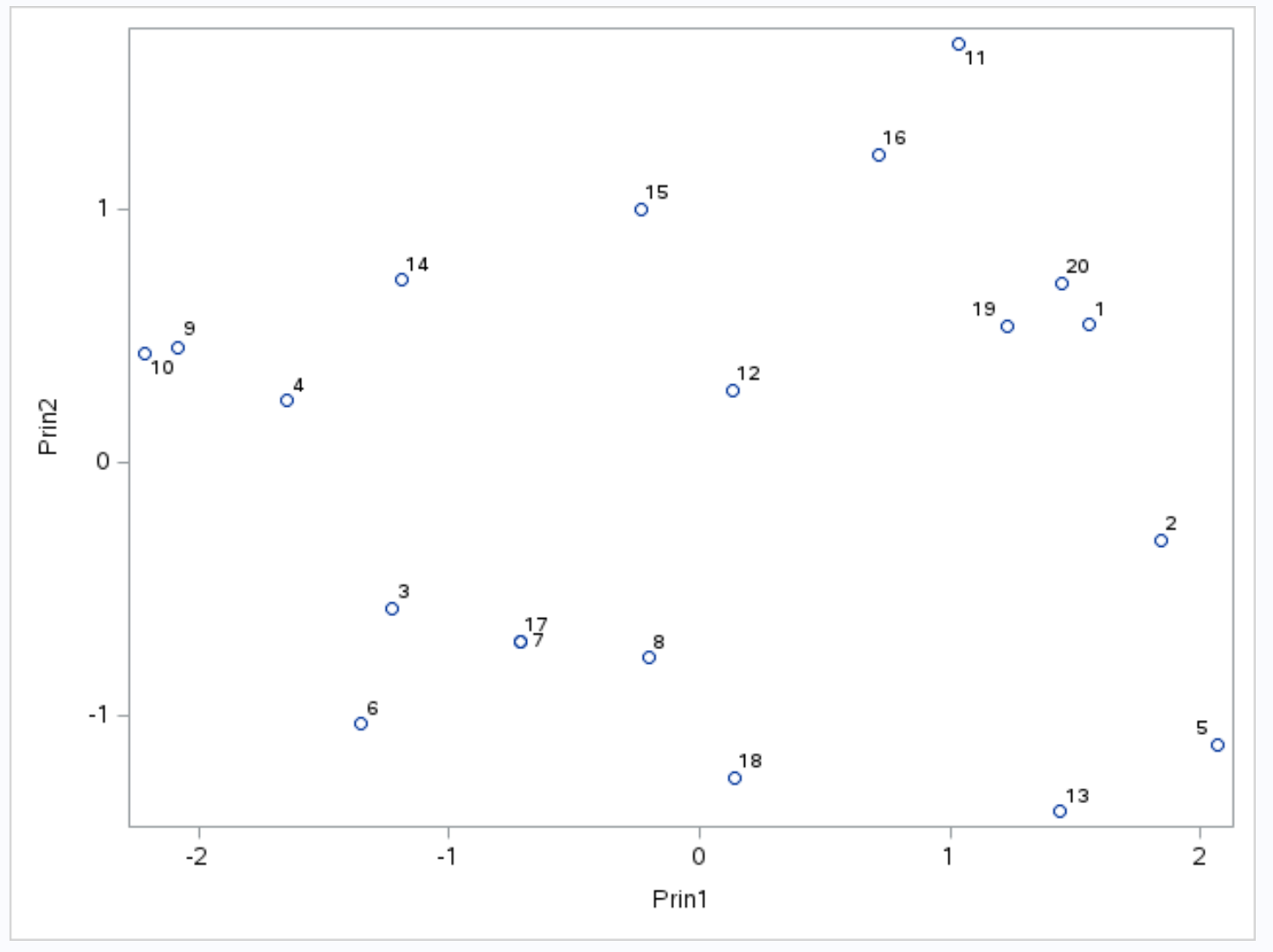
L’asse x mostra la prima componente principale, l’asse y mostra la seconda componente principale e le singole osservazioni del set di dati vengono visualizzate all’interno del grafico come piccoli cerchi.

Le osservazioni che si affiancano nel grafico hanno valori simili per le tre variabili di punti , assist e rimbalzi .

Ad esempio, all’estrema sinistra del grafico, possiamo vedere che le osservazioni n. 9 e n. 10 sono estremamente vicine tra loro.

Se facciamo riferimento al set di dati originale, possiamo vedere i seguenti valori per queste osservazioni:

• Osservazione n°9 : 2 punti, 5 assist, 17 rimbalzi
• Osservazione n. 10 : 4 punti, 5 assist, 19 rimbalzi

I valori sono simili per ciascuna delle tre variabili, il che spiega perché queste osservazioni sono così vicine tra loro sul biplot.

Abbiamo anche visto nella tabella dei risultati intitolata Autovalori della matrice di correlazione che i primi due componenti principali rappresentano l’ 88,21% della variazione totale nel set di dati.

Poiché questa percentuale è molto alta, è valido analizzare quali osservazioni nel biplot sono vicine tra loro, perché le due componenti principali che compongono il biplot rappresentano quasi tutta la variazione nel set di dati.

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in SAS:

Come eseguire una regressione lineare semplice in SAS
Come eseguire la regressione lineare multipla in SAS
Come eseguire la regressione logistica in SAS