Analisi discriminante lineare in r (passo dopo passo)

L’analisi discriminante lineare è un metodo che è possibile utilizzare quando si dispone di un insieme di variabili predittive e si desidera classificare una variabile di risposta in due o più classi.

Questo tutorial fornisce un esempio passo passo di come eseguire l’analisi discriminante lineare in R.

Passaggio 1: caricare le librerie necessarie

Innanzitutto, caricheremo le librerie necessarie per questo esempio:

 library (MASS)
library (ggplot2)

Passaggio 2: caricare i dati

Per questo esempio, utilizzeremo il set di dati dell’iride integrato in R. Il codice seguente mostra come caricare e visualizzare questo set di dati:

 #attach iris dataset to make it easy to work with
attach(iris)

#view structure of dataset
str(iris)

'data.frame': 150 obs. of 5 variables:
 $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
 $ Sepal.Width: num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
 $Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
 $Petal.Width: num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
 $ Species: Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 ...

Possiamo vedere che il set di dati contiene 5 variabili e 150 osservazioni in totale.

Per questo esempio, costruiremo un modello di analisi discriminante lineare per classificare a quale specie appartiene un dato fiore.

Utilizzeremo le seguenti variabili predittive nel modello:

• Lunghezza.sepalo
• Sepalo.Larghezza
• Petalo.Lunghezza
• Petalo.Larghezza

E li useremo per prevedere la variabile di risposta Specie , che supporta le seguenti tre classi potenziali:

• setosa
• versicolor
• Virginia

Passaggio 3: ridimensionare i dati

Uno dei presupposti chiave dell’analisi discriminante lineare è che ciascuna delle variabili predittive abbia la stessa varianza. Un modo semplice per garantire che questa ipotesi sia soddisfatta è ridimensionare ciascuna variabile in modo tale che abbia una media pari a 0 e una deviazione standard pari a 1.

Possiamo farlo rapidamente in R usando la funzione scale() :

 #scale each predictor variable (ie first 4 columns)
iris[1:4] <- scale(iris[1:4])

Possiamo utilizzare la funzione apply() per verificare che ciascuna variabile predittrice abbia ora una media pari a 0 e una deviazione standard pari a 1:

 #find mean of each predictor variable
apply(iris[1:4], 2, mean)

 Sepal.Length Sepal.Width Petal.Length Petal.Width 
-4.484318e-16 2.034094e-16 -2.895326e-17 -3.663049e-17 

#find standard deviation of each predictor variable
apply(iris[1:4], 2, sd) 

Sepal.Length Sepal.Width Petal.Length Petal.Width 
           1 1 1 1

Passaggio 4: creare campioni di formazione e test

Successivamente, divideremo il set di dati in un set di training su cui addestrare il modello e un set di test su cui testare il modello:

 #make this example reproducible
set.seed(1)

#Use 70% of dataset as training set and remaining 30% as testing set
sample <- sample(c( TRUE , FALSE ), nrow (iris), replace = TRUE , prob =c(0.7,0.3))
train <- iris[sample, ]
test <- iris[!sample, ] 

Passaggio 5: modificare il modello LDA

Successivamente, utilizzeremo la funzione lda() del pacchetto MASS per adattare il modello LDA ai nostri dati:

 #fit LDA model
model <- lda(Species~., data=train)

#view model output
model

Call:
lda(Species ~ ., data = train)

Prior probabilities of groups:
    setosa versicolor virginica 
 0.3207547 0.3207547 0.3584906 

Group means:
           Sepal.Length Sepal.Width Petal.Length Petal.Width
setosa -1.0397484 0.8131654 -1.2891006 -1.2570316
versicolor 0.1820921 -0.6038909 0.3403524 0.2208153
virginica 0.9582674 -0.1919146 1.0389776 1.1229172

Coefficients of linear discriminants:
                    LD1 LD2
Sepal.Length 0.7922820 0.5294210
Sepal.Width 0.5710586 0.7130743
Petal.Length -4.0762061 -2.7305131
Petal.Width -2.0602181 2.6326229

Proportion of traces:
   LD1 LD2 
0.9921 0.0079 

Ecco come interpretare i risultati del modello:

Probabilità a priori del gruppo: rappresentano le proporzioni di ciascuna specie nel set di addestramento. Ad esempio, il 35,8% di tutte le osservazioni nel training set riguardavano la specie virginica .

Medie di gruppo: mostrano i valori medi di ciascuna variabile predittrice per ciascuna specie.

Coefficienti discriminanti lineari: mostrano la combinazione lineare delle variabili predittive utilizzate per addestrare la regola decisionale del modello LDA. Per esempio:

• LD1: 0,792 * lunghezza sepalo + 0,571 * larghezza sepalo – 4,076 * lunghezza petalo – 2,06 * larghezza petalo
• LD2: 0,529 * lunghezza sepalo + 0,713 * larghezza sepalo – 2,731 * lunghezza petalo + 2,63 * larghezza petalo

Proporzione traccia: visualizza la percentuale di separazione raggiunta da ciascuna funzione discriminante lineare.

Passaggio 6: utilizzare il modello per fare previsioni

Una volta adattato il modello utilizzando i nostri dati di addestramento, possiamo utilizzarlo per fare previsioni sui nostri dati di test:

 #use LDA model to make predictions on test data
predicted <- predict (model, test)

names(predicted)

[1] "class" "posterior" "x"   

Ciò restituisce una lista con tre variabili:

• classe: la classe prevista
• posteriore: la probabilità a posteriori che un’osservazione appartenga a ciascuna classe
• x: Discriminanti lineari

Possiamo visualizzare rapidamente ciascuno di questi risultati per le prime sei osservazioni nel nostro set di dati di test:

 #view predicted class for first six observations in test set
head(predicted$class)

[1] setosa setosa setosa setosa setosa setosa
Levels: setosa versicolor virginica

#view posterior probabilities for first six observations in test set
head(predicted$posterior)

   setosa versicolor virginica
4 1 2.425563e-17 1.341984e-35
6 1 1.400976e-21 4.482684e-40
7 1 3.345770e-19 1.511748e-37
15 1 6.389105e-31 7.361660e-53
17 1 1.193282e-25 2.238696e-45
18 1 6.445594e-22 4.894053e-41

#view linear discriminants for first six observations in test set
head(predicted$x)

         LD1 LD2
4 7.150360 -0.7177382
6 7.961538 1.4839408
7 7.504033 0.2731178
15 10.170378 1.9859027
17 8.885168 2.1026494
18 8.113443 0.7563902

Possiamo utilizzare il seguente codice per vedere per quale percentuale di osservazioni il modello LDA ha predetto correttamente la specie:

 #find accuracy of model
mean(predicted$class==test$Species)

[1] 1

Si scopre che il modello ha predetto correttamente la specie per il 100% delle osservazioni nel nostro set di dati di test.

Nel mondo reale, un modello LDA raramente prevede correttamente i risultati di ciascuna classe, ma questo set di dati dell’iride è semplicemente costruito in modo tale che gli algoritmi di apprendimento automatico tendono a funzionare molto bene.

Passaggio 7: visualizzare i risultati

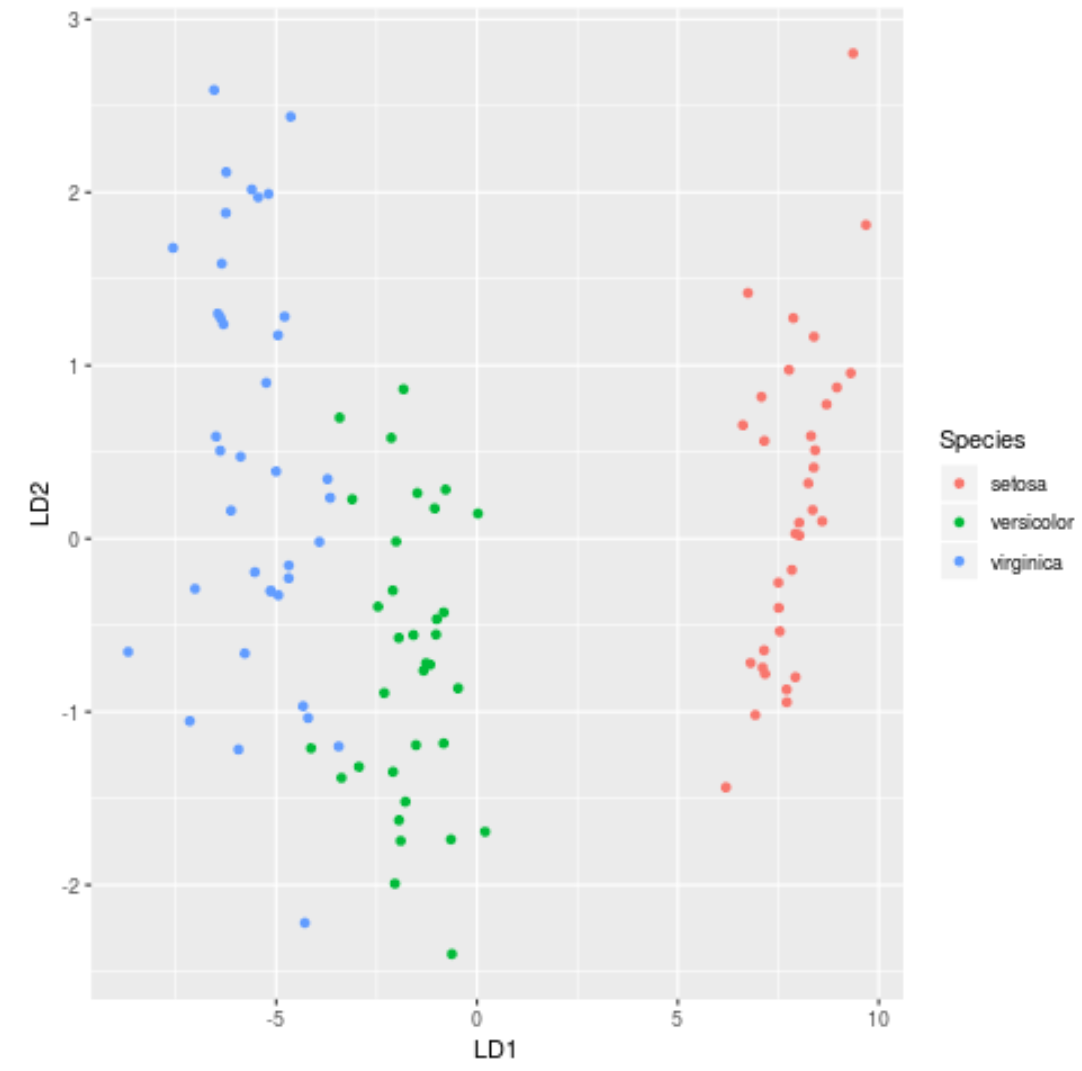
Infine, possiamo creare un grafico LDA per visualizzare i discriminanti lineari del modello e quanto bene separa le tre diverse specie nel nostro set di dati:

 #define data to plot
lda_plot <- cbind(train, predict(model)$x)

#createplot
ggplot(lda_plot, aes (LD1, LD2)) +
  geom_point( aes (color=Species))

Puoi trovare il codice R completo utilizzato in questo tutorial qui .